Đề kiểm tra Cuối chương 3 (có lời giải) - Đề 5
21 câu hỏi
Phần I: Trắc nghiệm nhiều phương án (12 câu-3điểm)
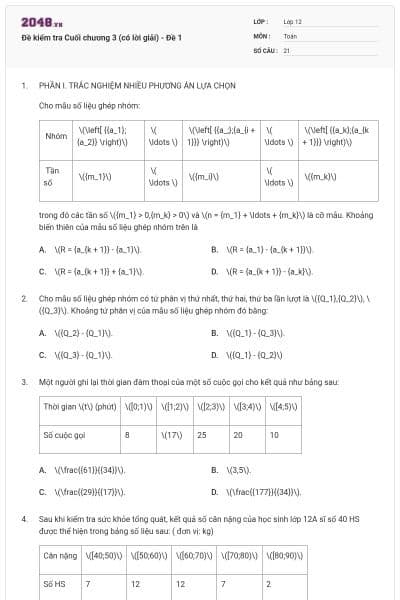
Khảo sát thời gian xem ti vi trong một ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
![]()
Nhóm chứa tứ phân vị thứ nhất là
\(\left[ {0;20} \right)\).
\(\left[ {20;40} \right)\).
\(\left[ {40;60} \right)\).
\(\left[ {60;80} \right)\).
Cô Hà thống kê lại đường kính thân gỗ của một số cây xoan đào 6 năm tuổi được trồng ở một lâm trường ở bảng sau.
Đường kính \((cm)\) | \([40;45)\) | \([45;50)\) | \([50;55)\) | \([55;60)\) | \([60;65)\) |
Tần số | 5 | 20 | 18 | 7 | 3 |
Hãy tìm khoảng biến thiên của mẫu số liệu ghép nhóm trên.
25.
30.
6.
69,8.
Bạn Chi rất thích nhảy hiện đại. Thời gian tập nhảy mỗi ngày trong thời gian gần đây của bạn Chi được thống kê lại ở bảng sau:
Thời gian (phút) | \([20;25)\) | \([25;30)\) | \([30;35)\) | \([35;40)\) | \([40;45)\) |
Só ngày | 6 | 6 | 4 | 1 | 1 |
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là
23,75.
27,5.
31,88.
8,125.
Trong dịp nghỉ hè bạn Lan rất thích đi bơi. Thời gian đi bơi mỗi ngày trong thời gian gần đây của bạn Lan được thống kê lại ở bảng sau:
Thời gian (phút) | \[\left[ {30\,;\,35} \right)\] | \[\left[ {35\,;\,40} \right)\] | \[\left[ {45\,;\,50} \right)\] | \[\left[ {50\,;\,55} \right)\] | \[\left[ {55\,;\,60} \right)\] |
Số ngày | 3 | 6 | 4 | 8 | 4 |
Nhóm chứa tứ phân vị thứ nhất \({Q_1}\) là
\[\left[ {30\,;\,35} \right)\].
\[\left[ {35\,;\,40} \right)\].
\[\left[ {45\,;\,50} \right)\].
\[\left[ {50\,;\,55} \right)\].
Khảo sát thời gian tập nghe nhạc trong ngày của học sinh lớp 12B thu được mẫu số liệu ghép nhóm sau:
Thời gian (phút) | \[\left[ {0;\,20} \right)\] | \[\left[ {20\,;\,40} \right)\] | \[\left[ {40;\,60} \right)\] | \[\left[ {60\,;\,80} \right)\] | \[\left[ {80\,;\,100} \right)\] |
Số học sinh | 5 | 10 | 12 | 9 | 4 |
Nhóm chứa tứ phân vị thứ ba \({Q_3}\) là
\[\left[ {20\,;\,40} \right)\].
\[\left[ {40;\,60} \right)\].
\[\left[ {60\,;\,80} \right)\].
\[\left[ {80\,;\,100} \right)\].
Một nhóm học sinh thi nhau giải khối rubik \(4 \times 4\). Thời gian hoàn thành của nhóm học sinh được thống kê trong bảng sau:
Thời gian giải rubik (giây) | [8; 10) | [10; 12) | [12; 14) | [14; 16) | [16; 18) |
Số học sinh | 4 | 6 | 8 | 4 | 3 |
Tìm tứ phân vị thứ nhất và tứ phân vị thứ ba của mẫu số liệu.
\({Q_1} = 10,75;\,{Q_3} = 14,375\).
\({Q_1} = 11,0625;\,{Q_3} = 14,375\).
\({Q_1} = 10,75;\,{Q_3} = 13,83\).
\({Q_1} = 10,85;\,{Q_3} = 14,75\).
Mỗi ngày bác Hương đều đi bộ để rèn luyện sức khoẻ. Quãng đường đi bộ mỗi ngày (đơn vị: \(km\)) của bác Hương trong 20 ngày được thống kê lại ở bảng sau:
Quãng đường \((km)\) | \([2,7;3,0)\) | \([3,0;3,3)\) | \([3,3;3,6)\) | \([3,6;3,9)\) | \([3,9;4,2)\) |
Số ngày | 3 | 6 | 5 | 4 | 2 |
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là
\(0,9\).
\(0,975\).
\(0,5\).
\(0,575\).
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):
Doanh thu | \([5;7)\) | \([7;9)\) | \([9;11)\) | \([11;13)\) | \([13;15)\) |
Số ngày | 2 | 7 | 7 | 3 | 1 |
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
\([7;9)\).
\([9;11)\).
\([11;13)\).
\([13;15)\).
Một siêu thị thống kê số tiền (đơn vị: chục nghìn đồng) mà 44 khách hàng mua hàng ở siêu thị đó trong một ngày. Số liệu được ghi lại trong Bảng 18.
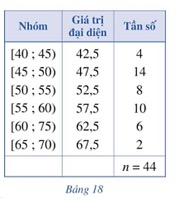
Phương sai của mẫu số liệu ghép nhóm trên là:
53,2.
46,1.
30.
11.
Khảo sát chiều cao ( đơn vị \(cm\)) của học sinh lớp 12A, ta thu được kết quả như sau:
Kết quả đo (\(cm\)) | \(\left[ {150;155} \right)\) | \(\left[ {155;160} \right)\) | \(\left[ {160;165} \right)\) | \(\left[ {165;170} \right)\) | \(\left[ {170;175} \right)\) |
Số học sinh | \(6\) | 10 | 14 | 5 | 5 |
Độ lệch chuẩn của mẫu số liệu ghép nhóm trên thuộc khoảng nào sau đây:
\(\left( {5,5;6} \right)\).
\(\left( {6;6,5} \right)\).
\(\left( {6,5;7} \right)\).
\(\left( {7;7,5} \right)\).
Có bao nhiêu nhận xét đúng trong các nhận xét sau :
1.Khoảng biến thiên của mẫu số liệu ghép nhóm luôn luôn bằng khoảng biến thiên của mẫu số liệu gốc.
2.Khoảng biến thiên của mẫu số liệu ghép nhóm được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm.
3.Khoảng biến thiên của mẫu số liệu ghép nhóm càng lớn thì mẫu số liệu càng phân tán.
\(0\).
\(1\).
\(2\).
\(3\).
Nhận xét nào sai trong các nhận xét sau :
1.Khoảng tứ phân vị của mẫu số liệu ghép nhóm bị ảnh hưởng bởi các giá trị bất thường trong mẫu số liệu.
2.Khoảng tứ phân vị của mẫu số liệu ghép nhóm xấp xỉ cho khoảng tứ phân vị của mẫu số liệu gốc.
3.Khoảng tứ phân vị càng lớn thì mã̃u số liệu càng phân tán.
4.Khoảng tứ phân vị được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm.
Nhận xét 1.
Nhận xét 2.
Nhận xét 3.
Nhận xét 4.
Phần II: Trắc nghiệm đúng-sai (5 câu-5 điểm)
Số tiền thưởng cuối năm của nhân viên công ty X được thống kê như sau (đơn vị triệu đồng):
3 | 5 | 7 | 12 | 15 | 11 | 4 | 5 | 8 | 15 |
16 | 18 | 20 | 22 | 15 | 29 | 28 | 22 | 24 | 26 |
16 | 21 | 25 | 26 | 29 | 6 | 8 | 10 | 17 | 18 |
a, Hãy chuyển mẫu số liệu sang dạng ghép nhóm với 6 nhóm có độ dài bằng nhau.
b, Các câu sau là Đúng hay Sai? (làm tròn kết quả đến hàng phần mười)
b1, Tiền thưởng trung bình của các nhân viên là \(16,2\).
b2, Khoảng biến thiên của mẫu số liệu ghép nhóm là 26.
b3, Khoảng tứ phân vị của mẫu số liệu ghép nhóm là \(14,5\).
Bảng 1 biểu diễn mẫu số liệu ghép nhóm về nhiệt độ (\({}^0C\)) của tỉnh Nghệ An tháng 5 năm 2024
Nhóm | Giá trị đại diện | Tần số | Tần số tích lũy |
\(\left[ {29;31} \right)\) | 30 | 1 | 1 |
\(\left[ {31;33} \right)\) | 32 | 4 | 5 |
\(\left[ {33;35} \right)\) | 34 | 5 | 10 |
\(\left[ {35;37} \right)\) | 36 | 13 | 26 |
\(\left[ {37;39} \right]\) | 38 | 7 | 33 |
|
| \(n = 30\) |
|
Trong mỗi ý a),b),c),d) chọn đúng hoặc sai ( làm tròn đến hàng phần trăm)
a) Nhóm \(\left[ {31;33} \right)\) có tần số bằng: 4
b) Mốt của mẫu số liệu ghép nhóm đã cho là: 13
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên bằng: 2,92
d) Phương sai của mẫu số liệu ghép nhóm trên bằng: 4,57
Cho bảng phân bố tần số ghép lớp cân nặng (đơn vị: kg) của các công nhân trong một công ty như sau:
![]()
Các mệnh đề sau đúng hay sai?
a) Tần suất của nhóm \[{\rm{[}}52;54)\] là: \(20\% \).
b) Số trung vị của mẫu số liệu là:\(54,909\,\).
c) Khoảng biến thiên của mẫu số liệu trên là: \(10\).
d) Độ lệch chuẩn của mẫu số liệu trên là: \(4,35\).
Cho bảng số liệu dưới đây về thời gian (phút) tập thể dục buổi sáng của hai bạn Bình và Chi trong 30 ngày.
Thời gian | \(\left[ {15;20} \right)\) | \(\left[ {20;25} \right)\) | \(\left[ {25;30} \right)\) | \(\left[ {30;35} \right)\) | \(\left[ {35;40} \right)\) |
Bạn Bình | \(5\) | \(8\) | \(10\) | \(4\) | \(3\) |
Bạn Chi | \(10\) | \(10\) | \(5\) | \(3\) | \(2\) |
Xét tính đúng sai của các khẳng định sau
a. Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập thể dục của Chi là 25 (phút).
b. Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bạn Bình là: \({Q_1} = \frac{{354}}{{16}}\)
c. Khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bạn Chi là
d. Phương sai của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bạn Bình là \(\frac{{314}}{9}\)
Bảng sau đây cho biết chiều cao của các em học sinh lớp 12A và 12B.
Chiều cao (cm) | \(\left[ {145\,;\,150} \right)\) | \(\left[ {150\,;\,155} \right)\) | \(\left[ {155\,;\,160} \right)\) | \(\left[ {160\,;\,165} \right)\) | \(\left[ {165\,;\,170} \right)\) | \(\left[ {170\,;\,175} \right)\) |
Số học sinh của lớp 12A | 2 | 1 | 15 | 11 | 9 | 3 |
Số học sinh của lớp 12B | 0 | 1 | 16 | 11 | 10 | 4 |
Các mệnh đề sau đúng hay sai?
a) Dựa vào khoảng biến thiên của mẫu số liệu ghép nhóm thì chiều cao của học sinh lớp 12A phân tán hơn lớp 12B.
b) Dựa vào khoảng tứ phân vị của mẫu số liệu ghép nhóm thì học sinh lớp 12A có chiều cao phân tán hơn học sinh lớp 12B.
c) Dựa vào phương sai của mẫu số liệu ghép nhóm thì chiều cao của học sinh lớp 12A ít phân tán hơn học sinh lớp 12B.
d) Học sinh lớp 12B có chiều cao đồng đều hơn học sinh lớp 12A vì có độ lệch chuẩn nhỏ hơn.
Phần III: Trả lời ngắn (4 câu-2điểm)
Bảng sau đây cho biết chiều cao của học sinh lớp 5A
Chiều cao (cm) | Tần số |
\(\left[ {85;\;90} \right)\) | \(1\) |
\(\left[ {90;\;95} \right)\) | \(4\) |
\(\left[ {95;\;100} \right)\) | \(8\) |
\(\left[ {100;\;105} \right)\) | \(12\) |
\(\left[ {105;\;110} \right)\) | \(3\) |
\(\left[ {110;\;115} \right)\) | \(2\) |
Tìm k hoảng biến thiên của mẫu số liệu ghép nhóm về chiều cao của học sinh lớp 5A.
Bảng sau đây cho biết chiều cao của học sinh lớp 5A
Chiều cao (cm) | Tần số |
\(\left[ {85;\;90} \right)\) | \(1\) |
\(\left[ {90;\;95} \right)\) | \(4\) |
\(\left[ {95;\;100} \right)\) | \(8\) |
\(\left[ {100;\;105} \right)\) | \(12\) |
\(\left[ {105;\;110} \right)\) | \(3\) |
\(\left[ {110;\;115} \right)\) | \(2\) |
Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm về chiều cao của học sinh lớp 5A.
Số người xem trong 60 buổi chiếu phim của một rạp chiếu phim nhỏ
Lớp người xem | Tần số |
[0, 10) [10, 20) [20, 30) [30, 40) [40, 50) [50, 60] | 5 9 11 15 12 8 |
Cộng | 60 |
Hãy tính phương sai của mẫu số liệu ghép nhóm trên (kết quả được làm tròn đến hàng phần chục)
Trả lời: ………………
Bảng dưới đây thống kê cự li ném tạ của một vận động viên.
Cự li (m) | \([19;19,5)\) | \([19,5;20)\) | \([20;20,5)\) | \([20,5;21)\) | \([21;21,5)\) |
Tần số | 13 | 45 | 24 | 12 | 6 |
Hãy tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả được làm tròn đến hàng phần trăm)
Trả lời: ………………