Đề kiểm tra Cuối chương 3 (có lời giải) - Đề 4
22 câu hỏi
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Xét mẫu số liệu cho bởi bảng sau. Khoảng biến thiên của mẫu số liệu ghép nhóm bằng
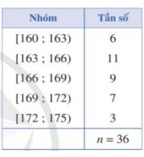
\(17\).
\(16\).
\(15\).
\(14\).
Xét mẫu số liệu cho bởi bảng sau:
Nhóm | Tần số |
[40; 45) | 4 |
[45; 50) | 11 |
[50; 55) | 9 |
[55; 60) |
|
[60; 65) | 8 |
| \(n\) = 40 |
Tần số \({n_4}\) của nhóm 4 trong mẫu số liệu trên bằng
\(9\).
\(8\).
\(7\).
\(10\).
Xét mẫu số liệu cho bởi bảng sau:
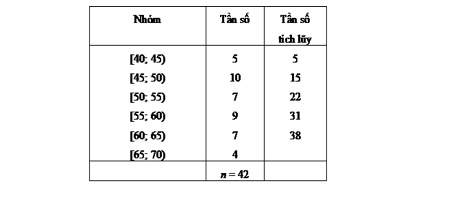
Tần số tích lũy của nhóm 6 bằng
\[40\].
\[42\]
\[44\].
\[46\].
Xét mẫu số liệu cho bởi bảng sau:
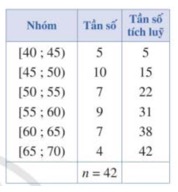
Tứ phân vị thứ nhất của mẫu số liệu trên bằng
\[47,5\].
\[47,75\]
\[48\].
\[48,25\].
Xét mẫu số liệu cho bởi bảng sau:
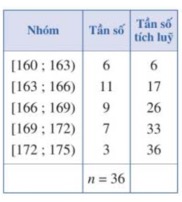
Tứ phân vị thứ hai của mẫu số liệu trên bằng
\[170\].
\[167\]
\[165\].
\[180\].
Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 20 con hổ và thu được kết quả như sau. Tứ phân vị thứ ba thuộc nhóm nào?
Tuổi thọ | \([14;15)\) | \([15;16)\) | \([16;17)\) | \([17;18)\) | \([18;19)\) |
Số con hổ | 1 | 3 | 8 | 6 | 2 |
\([15;16)\).
\([16;17)\).
\([17;18)\).
\([18;19)\).
Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:
Thời gian (phút) | \([9,5;12,5)\) | \([12,5;15,5)\) | \([15,5;18,5)\) | \([18,5;21,5)\) | \([21,5;24,5)\) |
Số học sinh | 3 | 12 | 15 | 24 | 2 |
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là
\(10,75.\)
\(4,75.\)
\(4,63.\)
\(4,38.\)
Điều tra về chiều cao của học sinh khối lớp 10, ta có kết quả sau:
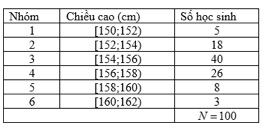
Giá trị đại diện của nhóm thứ tư là:
\[156,5.\]
\[157.\]
\[157,5.\]
\[158.\]
Các bạn học sinh lớp 12A1 trả lời 40 câu hỏi trong một bải kiểm tra. Kết quả được thống kê ở bảng sau. Hãy tính độ dài của mỗi nhóm.
Số câu trả lời đúng | \(\left[ {16;21} \right)\) | \(\left[ {21;26} \right)\) | \(\left[ {26;31} \right)\) | \(\left[ {31;36} \right)\) | \(\left[ {36;41} \right)\) |
Số học sinh | 4 | 6 | 8 | 18 | 4 |
\[2.\]
\[3.\]
\[4.\]
\[5.\]
Tìm cân nặng trung bình của học sinh lớp 11D cho trong bảng sau, làm tròn đến hàng phần trăm.
![]()
\[51,8\].
\[51,81\].
\[52\].
\[51,809\].
Tìm phương sai của mẫu số liệu ghép nhóm được cho ở bảng sau (làm tròn kết quả đến hàng phần mười)
Nhóm | Tần số |
\(\left[ {80;90} \right)\) | 5 |
\(\left[ {90;100} \right)\) | 7 |
\(\left[ {100;110} \right)\) | 8 |
\(\left[ {110;120} \right)\) | 8 |
\(\left[ {120;130} \right)\) | 12 |
| \(n = 40\) |
\(194,5\).
\(193,5\).
\(194,4\).
\(193,4\).
Tìm độ lệch chuẩn của mẫu số liệu ghép nhóm được cho ở bảng sau (làm tròn kết quả đến hàng phần mười)
Nhóm | Tần số |
\(\left[ {25;35} \right)\) | 10 |
\(\left[ {35;45} \right)\) | 7 |
\(\left[ {45;55} \right)\) | 5 |
\(\left[ {65;75} \right)\) | 9 |
\(\left[ {75;85} \right)\) | 9 |
| \(n = 40\) |
\[15,1\].
\[15,0\].
\[14,8\].
\[14,9\].
Cho bảng số liệu sau. Trả lời những câu hỏi được cho trong bảng, Đúng ghi Đ, Sai ghi S.
Nhóm | Tần số |
\(\left[ {115;125} \right)\) | 9 |
\(\left[ {125;135} \right)\) | 5 |
\(\left[ {135;145} \right)\) | 5 |
\(\left[ {145;155} \right)\) | 4 |
\(\left[ {155;165} \right)\) | 7 |
| \(n = 30\) |
Mệnh đề | Đúng/Sai |
a) Khoảng biến thiên của mẫu số liệu ghép trên là \(R = 165\). |
|
b) Tần số của nhóm 5 là 7. |
|
c) Tần số tích lũy của nhóm 3 là 10. |
|
d) Tần số tích lũy của nhóm 5 hơn nhóm 3 là 11. |
|
Cho bảng số liệu sau. Trả lời những câu hỏi được cho trong bảng, Đúng ghi Đ, Sai ghi S.
Nhóm | Tần số |
\(\left[ {15;25} \right)\) | 2 |
\(\left[ {25;35} \right)\) | 6 |
\(\left[ {35;45} \right)\) | 5 |
\(\left[ {45;55} \right)\) | 4 |
\(\left[ {55;65} \right)\) | 3 |
| \(n = 20\) |
Mệnh đề | Đúng/Sai |
a) Tứ phân vị thứ nhất của mẫu số liệu trên là: \({Q_1} = 50\). |
|
b) Tứ phân vị thứ hai của mẫu số liệu có giá trị nhỏ hơn 38. |
|
c) Tứ phân vị thứ hai của mẫu số liệu có giá trị nằm trong khoảng \(\left( {48,5;\,\,51,5} \right)\) |
|
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là \({\Delta _Q} = 20\). |
|
Một mẫu số liệu được cho ở dạng bảng tần số ghép nhóm như sau:
Nhóm | \([0,5;2,5)\) | \([2,5;4,5)\) | \([4,5;6,5)\) | \([6,5;8,5)\) | \([8,5;10,5)\) |
Tần số | 4 | 7 | 16 | 8 | 5 |
Các mệnh đề sau đúng hay sai?
Mệnh đề | Đúng | Sai | |
a) | Nhóm \([0,5;2,5)\) có giá trị đại diện là 1,5. |
|
|
b) | Nhóm \([4,5;6,5)\) có giá trị đại diện là 5,5. |
|
|
c) | Nhóm \([8,5;10,5)\) có độ dài lớn nhất trong các nhóm còn lại. |
|
|
d) | Số trung bình của mẫu số liệu trên là 5,5. |
|
|
Số cuộc điện thoại một người thực hiện mỗi ngày trong 30 ngày được lựa chọn ngẫu nhiên được thống kê trong bảng sau:
Số cuộc gọi | \([2,5;5,5)\) | \([5,5;8,5)\) | \([8,5;11,5)\) | \([11,5;14,5)\) | \([14,5;17,5)\) |
Số ngày | 5 | 13 | 7 | 3 | 2 |
Các mệnh đề sau đúng hay sai?
Mệnh đề | Đúng | Sai | ||
a) | Số trung bình của mẫu số liệu trên là 8,4. |
|
| |
b) | Phương sai của mẫu số liệu trên là 10,64. |
|
| |
c) | Độ lệch chuẩn của mẫu số liệu trên là 4,05. |
|
| |
d) | Độ dài nhóm của mẫu số liệu trên là 15,5. |
|
| |
Kết quả đo chiều cao của 250 cây dừa đột biến 3 năm tuổi ở một viện nghiên cứu được tổng hợp ở bảng sau:
Chiều cao \(\left( {{m^2}} \right)\) | \([8,5;8,8)\) | \([8,8;9,1)\) | \([9,1;9,4)\) | \([9,4;9,7)\) | \([9,7;10)\) |
Số cây | 36 | 45 | 83 | 65 | 21 |
Tìm khoảng biến thiên của mẫu số liệu ghép nhóm trên?
Một công ty bất động sản Đất Vàng thực hiện cuộc khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức giá nào để tiến hành dự án xây nhà ở Thăng Long group sắp tới. Kết quả khảo sát 500 khách hàng được ghi lại ở bảng sau:
Mức giá (triệu đồng) | \([10;14)\) | \([14;18)\) | \([18;22)\) | \([22;26)\) | \([26;30)\) |
Số khách hàng | 75 | 105 | 179 | 96 | 45 |
Tìm tần số tích lũy của nhóm \([18;22)\).
Bảng dưới đây biểu diễn mẫu số liệu ghép nhóm về chiều cao (đơn vị: Centimet) của 43 học sinh trong một lớp học khối 11 của một trường phổ thông
Nhóm | Tần số |
\(\left[ {150;155} \right)\) | 5 |
\(\left[ {155;160} \right)\) | 10 |
\(\left[ {160;165} \right)\) | 12 |
\(\left[ {165;170} \right)\) | 9 |
\(\left[ {170;175} \right)\) | 4 |
\(\left[ {175;180} \right)\) | 3 |
| \(n = 43\) |
Tứ phân vị thứ hai của mẫu số liệu ghép nhóm trên bằng (làm tròn đến hàng phần trăm)
Trả lời: ……………………………………….
Bảng dưới đây biểu diễn mẫu số liệu ghép nhóm về chiều cao (đơn vị: Centimet) của 43 học sinh trong một lớp học khối 11 của một trường phổ thông
Nhóm | Tần số |
\(\left[ {150;155} \right)\) | 5 |
\(\left[ {155;160} \right)\) | 10 |
\(\left[ {160;165} \right)\) | 12 |
\(\left[ {165;170} \right)\) | 9 |
\(\left[ {170;175} \right)\) | 4 |
\(\left[ {175;180} \right)\) | 3 |
| \(n = 43\) |
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên bằng (làm tròn đến hàng phần trăm)
Trả lời: ……………………………………….
Bảng dưới đây biểu diễn mẫu số liệu ghép nhóm về chiều cao (đơn vị: Centimet) của 43 học sinh trong một lớp học khối 11 của một trường phổ thông
Nhóm | Giá trị đại diện | Tần số |
\(\left[ {150;155} \right)\) | 152,5 | 5 |
\(\left[ {155;160} \right)\) | 157,5 | 10 |
\(\left[ {160;165} \right)\) | 162,5 | 12 |
\(\left[ {165;170} \right)\) | 167,5 | 9 |
\(\left[ {170;175} \right)\) | 172,5 | 4 |
\(\left[ {175;180} \right)\) | 177,5 | 3 |
|
| \(n = 43\) |
Số trung bình cộng của mẫu số liệu ghép nhóm trên bằng (làm tròn đến hàng phần trăm)
Trả lời: ……………………………………….
Bảng dưới đây biểu diễn mẫu số liệu ghép nhóm về chiều cao (đơn vị: Centimet) của 43 học sinh trong một lớp học khối 11 của một trường phổ thông
Nhóm | Giá trị đại diện | Tần số |
\(\left[ {150;155} \right)\) | 152,5 | 5 |
\(\left[ {155;160} \right)\) | 157,5 | 10 |
\(\left[ {160;165} \right)\) | 162,5 | 12 |
\(\left[ {165;170} \right)\) | 167,5 | 9 |
\(\left[ {170;175} \right)\) | 172,5 | 4 |
\(\left[ {175;180} \right)\) | 177,5 | 3 |
|
| \(n = 43\) |
Phương sai của mẫu số liệu ghép nhóm trên bằng (làm tròn đến hàng phần trăm)
Trả lời: ……………………………………….