Đề kiểm tra Cuối chương 3 (có lời giải) - Đề 3
23 câu hỏi
Phần I: Trắc nghiệm nhiều phương án (12 câu-3điểm)
Cho mẫu số liệu ghép nhóm
Nhóm | Tần số |
\(\left[ {{a_1};{a_2}} \right)\) \(\left[ {{a_2};{a_3}} \right)\) … \(\left[ {{a_m};{a_{m + 1}}} \right)\) | \({n_1}\) \({n_2}\) \({n_m}\)
|
| \(n\) |
Gọi \({Q_1},\,{Q_2},\,{Q_3}\)lần lượt là tứ phân vị thứ nhất, tứ phân vị thứ hai và tứ phân vị thứ ba của mẫu số liệu. Khoảng tứ phân vị của mẫu số liệu trên là
\({\Delta _Q} = {Q_3} - {Q_1}\).
\({\Delta _Q} = {Q_3} - {Q_2}\).
\({\Delta _Q} = {Q_2} - {Q_1}\).
\({\Delta _Q} = {Q_3} - \frac{3}{2}{Q_1}\)
Cho mẫu số liệu ghép nhóm
Nhóm | Tần số |
\(\left[ {{a_1};{a_2}} \right)\) \(\left[ {{a_2};{a_3}} \right)\) … \(\left[ {{a_m};{a_{m + 1}}} \right)\) | \({n_1}\) \({n_2}\) \({n_m}\)
|
| \(n\) |
Khoảng biến thiên của mẫu số liệu trên là
\(R = {a_m} - {a_1}\).
\(R = {a_{m + 1}} - {a_m}\).
\(R = {a_{m + 1}} - {a_2}\).
\(R = {a_{m + 1}} - {a_1}\)
Bảng thống kê chiều cao của 40 mẫu cây ở một vườn thực vật (đơn vị: centimét)
Khoảng biến thiên của mẫu số liệu trên bằng
\(R = 60\).
\(R = 50\).
\(R = 70\).
\(R = 10\)
ghi lại ở bảng sau:
Thời gian | \([9,5\,;\,12,5)\) | \([12,5\,;\,15,5)\) | \([15,5\,;\,18,5)\) | \([18,5\,;\,21,5)\) | \([21,5\,;\,24,5)\) |
Số học sinh | \(3\) | \(12\) | \(15\) | \(24\) | 2 |
Nhóm chứa tứ phân vị thứ nhất là
\([9,5\,;\,12,5)\).
\([12,5\,;\,15,5)\).
\([15,5\,;\,18,5)\).
\([18,5\,;\,21,5)\).
Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Thời gian (phút) | \([0\,;\,20)\) | \[[20\,;\,40)\] | \([40\,;\,60)\) | \([60\,;\,80)\) | \([80\,;\,100)\) |
Số học sinh | \(5\) | \(9\) | \(12\) | \(10\) | \(6\) |
Nhóm chứa tứ phân vị thứ ba là
\[[20\,;\,40)\].
\([40\,;\,60)\).
\([60\,;\,80)\).
\([80\,;\,100)\).
Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên của một công ty như sau:
Thời gian | \([15\,;\,20)\) | \[[20\,;\,25)\] | \([25\,;\,30)\) | \([30\,;\,35)\) | \([35\,;\,40)\) | \([40\,;\,45)\) | \([45\,;\,50)\) |
Số nhân viên | \(7\) | \(14\) | \(25\) | \(37\) | \(21\) | \(14\) | \(10\) |
Tứ phân vị thứ nhất \({Q_1}\) và tứ phân vị thứ ba \({Q_3}\) của mẫu số liệu ghép nhóm này là
\({Q_1} = \frac{{136}}{5}\,,\,{Q_3} = \frac{{800}}{{21}}\).
\({Q_1} = \frac{{1360}}{{37}}\,,\,{Q_3} = \frac{{800}}{{21}}\).
\({Q_1} = \frac{{1360}}{{37}}\,,\,{Q_3} = \frac{{3280}}{{83}}\).
\({Q_1} = \frac{{136}}{5}\,,\,{Q_3} = \frac{{3280}}{{83}}\).
Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:
![]()
Tìm tứ phân vị thứ nhất \({Q_1}\).
\({Q_1} = 15\).
\({Q_1} = 15,5\).
\({Q_1} = 15,2\).
\({Q_1} = 15,25\).
Thống kê cân nặng của học sinh lớp 11A cho trong bảng dưới đây:
Cân nặng | \(\left[ {40,5;45,5} \right)\) | \(\left[ {45,5;50,5} \right)\) | \(\left[ {50,5;55,5} \right)\) | \(\left[ {55,5;60,5} \right)\) | \(\left[ {60,5;65,5} \right)\) | \(\left[ {65,5;70,5} \right)\) |
Số học sinh | \(10\) | \(7\) | \(16\) | \(4\) | \(2\) | \(3\) |
Tính cân nặng trung bình của học sinh lớp 11A?
\[50,1\].
\[52,83\].
\[50,81\].
\[51,81\].
Phương sai của một mẫu số liệu ghép nhóm cho bởi bảng thống kê dưới đây là:
\(13,24\)
\(15,74\)
\(18,84\)
\(14,84\)
Kết quả khảo sát thời gian sử dụng liên tục (đơn vị: giờ) từ lúc sạc đầy cho đến khi hết của pin một số máy vi tính cùng loại được thống kê ở bảng sau:
Thời gian sử dụng | \(\left[ {7,2;7,4} \right)\) | \(\left[ {7,4;7,6} \right)\) | \(\left[ {7,6;7,8} \right)\) | \(\left[ {7,8;8,0} \right)\) |
Số máy | 2 | 4 | 7 | 6 |
Độ lệch chuẩn của mẫu số liệu ghép nhóm có giá trị gần nhất với giá trị nào dưới đây?
\(0,192\).
\(0,193\).
\(0,037\)
\(0,2\)
Đại lượng nào đo độ phân tán của nửa giữa của mẫu số liệu, không bị ảnh hưởng nhiều bởi các giá trị ngoại lệ trong mẫu số liệu?
Khoảng biến thiên.
Khoảng tứ phân vị.
Phương sai.
Độ lệch chuẩn.
Để so sánh mức độ phân tán của các mẫu số liệu ghép nhóm có cùng số trung bình ta dùng đại lượng nào?
Khoảng biến thiên.
Khoảng tứ phân vị.
Trung vị.
Độ lệch chuẩn.
Mẫu số liệu dưới đây ghi lại tốc độ của \(40\) ô tô khi đi qua một trạm đo tốc độ (đơn vị: km/h):

a) Bảng tần số ghép nhóm cho mẫu số liệu trên có sáu nhóm ứng với sáu nửa khoảng là
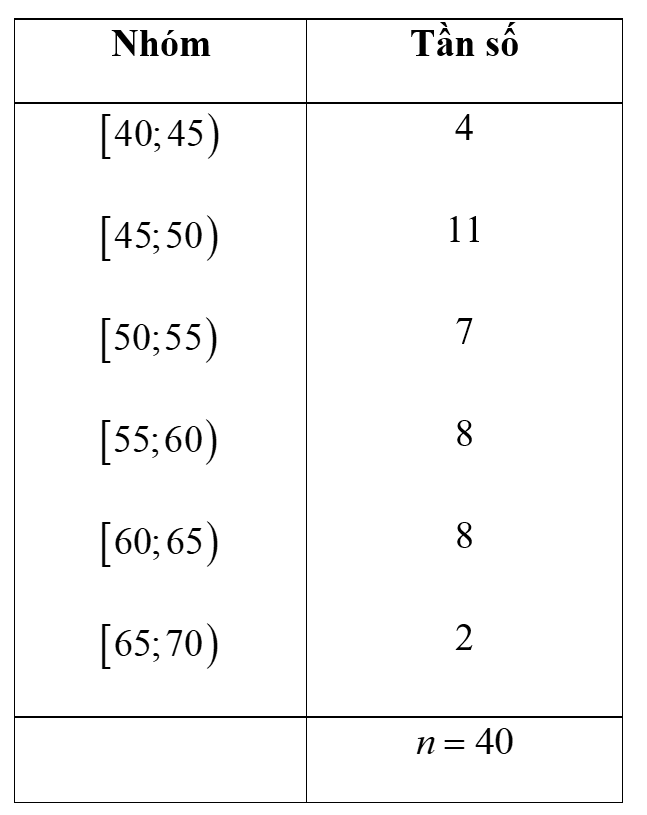
b) Mẫu số liệu trên có số trung bình là 54,875
c) Tứ phân vị của mẫu số liệu trên là: \({Q_1} = 47,8(km/h);{Q_2} = 53,6(km/h);{Q_3} = 60(km/h).\)
d) Khoảng biến thiên của mẫu số liệu trên là 25.
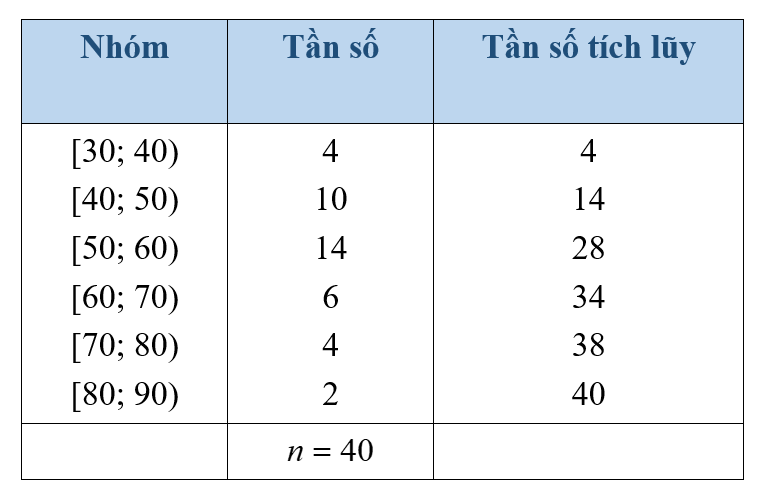
Bảng dưới đây cho ta bảng tần số ghép nhóm số liệu thống kê cân nặng của \(40\) học sinh lớp \(12{\rm{B}}\) trong một trường trung học phổ thông (đơn vị: kilôgam).
Nhóm | Số học sinh |
\(\left[ {30\,;\,40} \right)\) | \(2\) |
\(\left[ {40\,;\,50} \right)\) | \(10\) |
\(\left[ {50\,;\,60} \right)\) | \(16\) |
\(\left[ {60\,;\,70} \right)\) | \(8\) |
\(\left[ {70\,;\,80} \right)\) | \(2\) |
\(\left[ {80\,;\,90} \right)\) | \(2\) |
| \(n = 40\) |
Các mệnh đề sau đúng hay sai?
a) Số học sinh nặng dưới \(50\,kg\) là \(12\).
b) Mốt của mẫu số liệu ghép nhóm trên xấp xỉ bằng \(54,29\,(kg)\).
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là \(\frac{{39}}{2}.\)
d) Phương sai của mẫu số liệu ghép nhóm là \(128.\)
Trong một hội thao, thời gian chạy \(200m\) của một nhóm các vận động viên được ghi lại ở bảng sau:
![]()
Dựa vào bảng số liệu trên, em hãy xét tính đúng, sai của các mệnh đề sau:
a) Tần suất của nhóm vận động viên chạy trong khoảng thời gian từ \(22\)giây đến dưới \(22,5\) giây bằng \(30\% \).
b) Số trung vị của mẫu số liệu (làm tròn đến chữ số thập phân thứ 2) bằng \(22,67\).
c) Khoảng biến thiên của mẫu số liệu bằng \(R = 2\).
d) Độ lệch chuẩn của mẫu số liệu (làm tròn đến chữ số thập phân thứ 2) bằng \(0.28\).
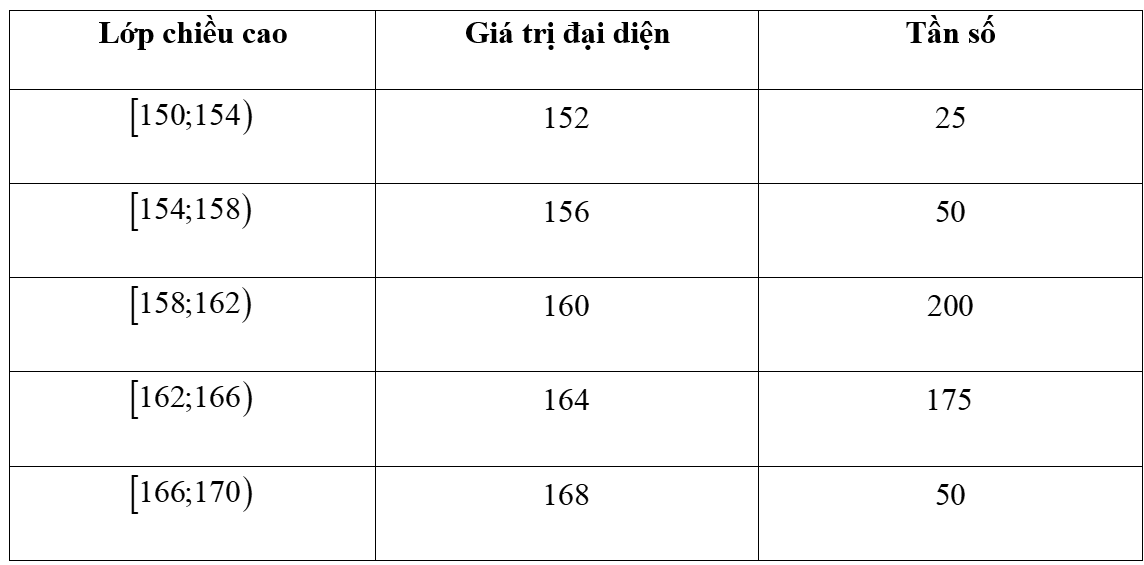
Thống kê chiều cao của tổ 1 và tổ 2 của lớp 10A cho bởi bảng sau:
Chiều cao (cm) | \(\left[ {150;155} \right)\) | \(\left[ {155;160} \right)\) | \(\left[ {160;165} \right)\) | \(\left[ {165;170} \right)\) | \(\left[ {170;175} \right)\) | \(\left[ {175;180} \right)\) |
Số học sinh tổ 1 | 3 | 2 | 2 | 1 | 3 | 0 |
Số học sinh tổ 2 | 1 | 3 | 3 | 2 | 1 | 1 |
A. Tứ phân vị thứ nhất của mẫu số liệu về chiều cao của học sinh tổ 1 là \({Q_1} = 154,375\).
B. Khoảng biến thiên của mẫu số liệu về chiều cao của học sinh tổ 1 là \(R = 25\).
C. Phương sai của mẫu số liệu về chiều cao của học sinh tổ 2 là \(s_2^2 \approx 48,88\).
D. Độ lệch chuẩn của mẫu số liệu về chiều cao của học sinh tổ 2 lớn hơn độ lệch chuẩn của mẫu số liệu về chiều cao của học sinh tổ 1.
Giả sử kết quả khảo sát hai khu vực \(A\) và \(B\) về độ tuổi kết hôn của một số phụ nữ vừa lập gia đình được cho ở bảng sau:
Tuổi kết hôn | \([19;22)\) | \([22;25)\) | \([25;28)\) | \([28;31)\) | \([31;34)\) |
Số phụ nữ khu vực \(A\) | 10 | 27 | 31 | 25 | 7 |
Số phụ nữ khu vực \(B\) | 47 | 40 | 11 | 2 | 0 |
Các mệnh đề sau đúng hay sai?
a) Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực A là: \(15\) (tuổi)
b) Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực B là: \(12\)(tuổi)
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm ứng với khu vực A là: \(\frac{{61}}{3}\) (tuổi)
d) Nếu so sánh theo khoảng tứ phân vị thì phụ nữ ở khu vực B có độ tuổi kết hôn đồng đều hơn
PHẦN III. TRẢ LỜI NGẮN
hời gian tập luyện trong một ngày (tính theo giờ) của một số vận động viên được ghi lại ở bảng sau:
Thời gian tập luyện | [0; 2) | [2; 4) | [4; 6) | [6; 8) | [8; 10) |
Số vận động viên | 3 | 8 | 12 | 12 | 4 |
Hãy tìm khoảng biến thiên cho thời gian tập luyện của các vận động viên.
Một trang báo điện tử thống kê thời gian người sử dụng đọc thông tin trên trang trong mỗi lần truy cập ở bảng sau:
Thời gian đọc (phút) | [0; 2) | [2; 4) | [4; 6) | [6; 8) | [8; 10) |
Số lượt truy cập | 45 | 34 | 23 | 18 | 5 |
Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.
Người ta ghi lại tiền lãi (đơn vị: triệu đồng) của một số nhà đầu tư (với số tiền đầu tư như nhau), khi đầu tư vào hai lĩnh vực \(A,B\) cho kết quả như sau:
Tiền lãi | \([5;10)\) | \([10;15)\) | \([15;20)\) | \([20;25)\) | \([25;30)\) |
Số nhà đầu tư vào lĩnh vực \(A\) | \(2\) | \(5\) | \(8\) | \(6\) | \(4\) |
Số nhà đầu tư vào lĩnh vực \(B\) | \(8\) | \(4\) | \(2\) | \(5\) | \(6\) |
Tính hiệu phương sai \(s_B^2 - s_A^2\) cho các mẫu số liệu về tiền lãi của các nhà đầu tư ở hai lĩnh vực này.
Thời gian hoàn thành một bài kiểm tra trắc nghiệm của một số học sinh lớp \(10\)của hai lớp \(10A\) và \(10B\) được ghi lại ở bảng sau:
Thời gian (phút) | \([6;7)\) | \([7;8)\) | \([8;9)\) | \([9;10)\) | \([10;11)\) |
Học sinh lớp \(10A\) | \(8\) | \(10\) | \(13\) | \(10\) | \(9\) |
Học sinh lớp \(10B\) | \(4\) | \(12\) | \(17\) | \(14\) | \(3\) |
Tính hiệu độ lệch chuẩn \({\sigma _{10A}} - {\sigma _{10B}}\).
Giá đóng cửa của một cổ phiếu là giá của cổ phiếu đó cuối một phiên giao dịch. Bảng sau thống kê giá đóng cửa (đơn vị: nghìn đồng) của hai mã cổ phiếu A và B trong 50 ngày giao dịch liên tiếp.
Giá đóng cửa | [120;122) | [122;124) | [124;126) | [126;128) | [128;130) |
Số ngày giao dịch của cổ phiếu A | 8 | 9 | 12 | 10 | 11 |
Số ngày giao dịch của cổ phiếu B | 16 | 4 | 3 | 6 | 21 |
Hãy tính phương sai của mẫu số liệu ghép nhóm trên và so sánh độ rủi ro của cổ phiếu A và cổ phiếu B.
Thầy Niên thống kê lại điểm trung bình cuối năm của các học sinh lớp 10A và 10B ở bảng sau.
Điểm trung bình | [5;6) | [6;7) | [7;8) | [8;9) | [9;10) |
Số học sinh lớp 10A | 1 | 0 | 11 | 22 | 6 |
Số học sinh lớp 10B | 0 | 6 | 8 | 14 | 12 |
Nếu so sánh theo độ lệch chuẩn thì học sinh lớp nào có điểm trung bình ít phân tán hơn?