Đề kiểm tra Cấp số cộng (có lời giải) - Đề 3
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho cấp số cộng \(\left( {{u_n}} \right)\)có \({u_1} = - 0,1;d = 0,1.\)Số hạng thứ \(7\)của cấp số cộng này là:
\(1,6.\).
\(6.\).
\(0,5.\).
\(0,6.\)
Cho cấp số cộng \[\left( {{u_n}} \right)\]thỏa mãn \[{u_1} = 4,\,\,{u_3} = 10.\]Công sai của cấp số cộng bằng
\(6.\).
\( - 6.\).
\(3.\).
\( - 3.\)
Cho cấp số cộng \[\left( {{u_n}} \right)\]với \[{u_5} = 11\]và \[{u_6} = 14\]. Công sai của cấp số cộng đã cho bằng
\[ - 6\].
\[3\].
\[12\].
\[6\].
Tìm tất cả các số thực \(x\) để ba số \({x^2}\),\({x^2} + 1\),\(3x\) theo thứ tự đó lập thành cấp số cộng?
\(x = 2\).
\(x \in \left\{ {1,2} \right\}\).
\(x = 0\).
\(x \in \left\{ {2,3} \right\}\).
Cho phương trình \({x^3} - 3{x^2} - 9x + m = 0\). Tìm m để phương trình có 3 nghiệm lập thành cấp số cộng.
16.
13.
12.
11.
Có tất cả bao nhiêu bộ số nguyên dương \[\left( {n,\,\,k} \right)\]biết \[n < 20\]và các số \[C_n^{k - 1}\], \[C_n^k\], \[C_n^{k + 1}\]theo thứ tự đó là số hạng thứ nhất, thứ ba, thứ năm của một cấp số cộng.
\[4\].
\[2\].
\[1\].
\({z_1} = a + 5i\).
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_4} = - 12\), \({u_{14}} = 18\). Tính tổng \[16\] số hạng đầu tiên của cấp số cộng này.
\({S_{16}} = - 24\).
\({S_{16}} = 26\).
\({S_{16}} = - 25\).
\({S_{16}} = 24\).
Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_n} = 3 - 2n\) thì \({S_{60}}\) bằng
\( - 6960\).
\( - 117\).
\( - 3840\).
\( - 116\).
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \(\left\{ {\begin{array}{*{20}{c}}{{u_2} + {u_5} = 42}\\{{u_4} + {u_9} = 66}\end{array}} \right.\). Tổng \(346\) số hạng đầu tiên của cấp số cộng trên là:
\[{S_{346}} = 422554\].
\[{S_{346}} = 242546\].
\[{S_{346}} = 156224\].
\[{S_{346}} = - 203558\].
Cho cấp số cộng \[\left( {{u_n}} \right)\] có \[{u_5} = - 15\], \[{u_{20}} = 60\]. Tổng \[{S_{20}}\] của \[20\] số hạng đầu tiên của cấp số cộng là
\[{S_{20}} = 600\].
\[{S_{20}} = 60\].
\[{S_{20}} = 250\].
\[{S_{20}} = 500\].
Cho cấp số cộng \[\left( {{u_n}} \right)\] có \({u_{2013}} + {u_6} = 1000\). Tổng \[2018\] số hạng đầu tiên của cấp số cộng đó là
\(1009000\).
\(100800\).
\(1008000\).
\(100900\).
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_5} = - 15\) và \({u_{20}} = 60\). Tổng của \(20\) số hạng đầu tiên của cấp số cộng đó là
\[{S_{20}} = 500\].
\[{S_{20}} = 250\].
\[{S_{20}} = 60\].
\[{S_{20}} = 600\].
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho cấp số cộng \(\left( {{u_n}} \right)\), biết rằng: \({u_1} = 5\) và tổng của 50 số hạng đầu bằng 5150 , khi đó:
a) Công sai của cấp số cộng bằng \(6\)
b) Số hạng \({u_{85}} = 341\)
c) Số hạng \({u_{10}} = 42\)
d) Tổng của 85 số hạng đầu \({S_{85}} = 14705\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_5} = 18\) và \(4{S_n} = {S_{2n}}\)
(trong đó \({S_n},{S_{2n}}\) theo thứ tự là tổng của \(n\) và \(2n\) số hạng đầu của cấp số cộng).
a) Số hạng đầu của cấp số cộng \(\left( {{u_n}} \right)\) bằng \(2\)
b) Công sai của cấp số cộng \(\left( {{u_n}} \right)\) bằng \(3\)
c) Số hạng \({u_{15}} = 58\)
b) Tổng 15 số hạng đầu của cấp số cộng bằng \(350\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) có công sai \(d < 0\) thoả mãn \(\left\{ {\begin{array}{*{20}{l}}{{u_1} + {u_7} = 26}\\{u_2^2 + u_6^2 = 466}\end{array}} \right.\). Khi đó:
a) Số hạng \({u_1} = 25\)
b) Công sai \(d = - 3\)
c) Số hạng \({u_{10}} = - 11\)
d) Số hạng \({u_{2024}} = - 8067\)
Xác định tính đúng, sai của các khẳng định sau:
a) Dãy số \(\left( {{u_n}} \right)\) với \(\frac{{ - 2}}{3};\frac{{ - 1}}{3};0;\frac{1}{3};\frac{2}{3};1;\frac{4}{3}\) là cấp số cộng với \({u_1} = \frac{{ - 2}}{3};d = \frac{1}{3}\).
b) Dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 7 - 3n\) là cấp số cộng với \({u_1} = 4;d = - 3\).
c) Dãy số \(\left( {{u_n}} \right)\) với \({u_n} = {n^2} + n + 1\) là cấp số cộng với \({u_1} = 3;d = 1\).
d) Dãy số \(\left( {{u_n}} \right)\) với \({u_n} = {( - 1)^n} + 3n\) không là cấp số cộng.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Định x để 3 số \(10 - 3x,2{x^2} + 3,7 - 4x\) theo thứ tự đó lập thành 1 cấp số cộng.
Một cấp số cộng có số hạng đầu bằng 5 và công sai bằng 2. Hỏi phải lấy tổng của bao nhiêu số hạng đầu của cấp số cộng này để có tổng bằng \(2700?\)
Một kiến trúc sư thiết kế một hội trường với 15 ghế ngồi ở hàng thứ nhất, 18 ghế ngồi ở hàng thứ hai, 21 ghế ngồi ở hàng thứ ba, và cứ như vậy . Nếu muốn hội trường đó có sức chứa ít nhất 870 ghế ngồi thì kiến trúc sư đó phải thiết kế tối thiểu bao nhiêu hàng ghế?
Anh Nam được nhận vào làm việc ở một công ty về công nghệ với mức lương khởi điểm là 100 triệu đồng một năm. Công ty sẽ tăng thêm lương cho anh Nam mỗi năm là 20 triệu đồng. Tính tổng số tiền lương mà anh Nam nhận được sau 10 năm làm việc cho công ty đó.
Một bức tường trang trí có dạng hình thang, rộng \(2,4\;m\) ở đáy và rộng \(1,2\;m\) ở đỉnh.
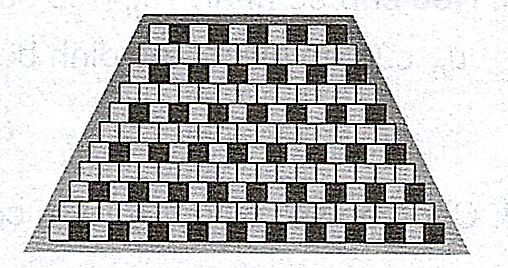
Các viên gạch hình vuông có kích thước \(10\;cm \times 10\;cm\) phải được đặt sao cho mỗi hàng ở phía trên chứa ít hơn một viên so với hàng ở ngay phía dưới nó. Hỏi sẽ cần bao nhiêu viên gạch hình vuông như vậy để ốp hết bức tường đó?
Có bao nhiêu hàng ghế trong một góc khán đài của một sân vận động, biết rằng góc khán đài đó có 2040 chỗ ngồi, hàng ghế đầu tiến có 10 chố ngồi và mỗi hàng ghế sau có thêm 4 chỗ ngồi so với hàng ghế ngay trước nó?








