Đề kiểm tra Cấp số cộng (có lời giải) - Đề 1
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Trong các dãy số \(\left( {{u_n}} \right)\) với số hạng tổng quát sau, dãy số nào là cấp số cộng?
\({u_n} = {3^n}\).
\({u_n} = 1 - 3n\).
\({u_n} = {3^n} + 1\).
\({u_n} = 3 + {n^2}\).
Cho cấp số cộng \(\left( {{u_n}} \right)\) biết \({u_1} = \frac{1}{3};{u_8} = 26\). Công sai \(d\) của cấp số cộng đó là:
\(\frac{{11}}{3}\).
\(\frac{{10}}{3}\).
\(\frac{3}{{10}}\).
\(\frac{3}{{11}}\).
Viết ba số hạng xen giữa các số 2 và 22 để được một cấp số cộng có năm số hạng. Ba số hạng đó lần lượt là:
\(7;12;17\).
\(6;10;14\).
\(8;13;18\).
\[6;12;18.\]
Cho cấp số cộng \(\left( {{u_n}} \right)\) biết \({u_5} + {u_7} = 19\). Giá trị của \({u_2} + {u_{10}}\) là:
38.
29.
12.
19.
Cho \(\left( {{u_n}} \right)\) là cấp số cộng có số hạng đầu \({u_1} = 2\), công sai \(d = - 5\). Tổng 10 số hạng đầu của cấp số cộng đó là:
\[ - 410\].
\[ - 205\].
245.
\[ - 230\].
Viết ba số hạng xen giữa các số \(2\) và 22 để được một cấp số cộng có năm số hạng.
7; 12; 17,
6; 10; 14.
8; 13; 18.
6; 12; 18.
Cho \(a,b,c\)theo thứ tự này là ba số hạng liên tiếp của một cấp số cộng. Biết \(a + b + c = 15\). Giá trị của \(b\)bằng
\(10\).
\(8\).
\(5\).
\(6\).
Bốn số \(x,\,\, - 2,\,\,y,\,\,6\) theo thứ tự đó lập thành một cấp số cộng. Khẳng định nào sau đây đúng?
\(x = - 6;y = 3\).
\(x = - 5;y = 3\).
\(x = - 6;y = 2\).
\(x = - 5;y = 2\).
Cho cấp số cộng có số hạng đầu\({u_1} = - \frac{1}{2},\) công sai \(d = \frac{1}{2}.\) Năm số hạng liên tiếp đầu tiên của cấp số này là:
\( - \frac{1}{2};0;1;\frac{1}{2};1.\)
\( - \frac{1}{2};0;\frac{1}{2};0;\frac{1}{2}.\)
\(\frac{1}{2};1;\frac{3}{2};2;\frac{5}{2}.\)
\( - \frac{1}{2};0;\frac{1}{2};1;\frac{3}{2}.\)
Cho hai số \( - 3\) và 23. Xen kẽ giữa hai số đã cho \(n\) số hạng để tất cả các số đó tạo thành cấp số cộng có công sai \(d = 2.\) Tìm n.
\(n = 12.\)
\(n = 13.\)
\(n = 14.\)
\(n = 15.\)
Tìm công sai \[d\] của cấp số cộng hữu hạn biết số hạng đầu \[{u_1} = 10\] và số hạng cuối \[{u_{21}} = 50\].
\(d = 3\).
\(d = 2\).
\(d = 4\).
\(d = - 2\).
Cho cấp số cộng \(({u_n})\)có \({u_1} = 4;\,{u_2} = 1\). Giá trị của \({u_{10}}\)bằng
\({u_{10}} = - 31\).
\({u_{10}} = - 23\).
\({u_{10}} = - 20\).
\({u_{10}} = 15\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho dãy số hữu hạn gồm các số hạng: \( - 1;2;5;8;11;14;17\). Khi đó:
a) Dãy số đã cho là không phải cấp số cộng.
b) Số hạng \({u_1} = - 1\)
c) Nếu dãy số đã cho là một cấp số cộng thì công sai của cấp số cộng là \(d = 2\)
d) Tổng tất cả số hạng của dãy số bằng \(56\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = \frac{3}{2}\), công sai \(d = \frac{1}{2}\). Khi đó:
a) Công thức cho số hạng tổng quát \({u_n} = 1 + \frac{n}{3}\)
b) 5 là số hạng thứ 8 của cấp số cộng đã cho
c) \(\frac{{15}}{4}\) một số hạng của cấp số cộng đã cho
d) Tổng 100 số hạng đầu của cấp số cộng \(\left( {{u_n}} \right)\) bằng \(2620\)
Cho các dãy số có số hạng tổng quát \({a_n} = 4n - 3\);\({b_n} = \frac{{2 - 3n}}{4}\); \({c_n} = {n^2}\). Khi đó
a) \(\left( {{a_n}} \right)\) là một cấp số cộng với số hạng đầu \({a_1} = 1\)
b) \(\left( {{a_n}} \right)\) là một cấp số cộng với công sai \(d = 4\).
c) \(\left( {{b_n}} \right)\) là một cấp số cộng với số hạng đầu \({b_1} = - \frac{1}{4}\) và công sai \(d = \frac{3}{4}\)
d) \(\left( {{c_n}} \right)\) là một cấp số cộng với công sai \(d = 2\)
Cho cấp số cộng \( - 2;x;6;y\). Khi đó
a) \(x = 2\)
b) \(y = 8\)
c) \({\rm{ }}P = y - x = 6\)
d) \({\rm{ }}P = {x^2} + {y^2} = 104.\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho ba số \(\frac{1}{{b + c}},\frac{1}{{c + a}},\frac{1}{{a + b}}\) theo thứ tự lập thành cấp số cộng. Chứng minh rằng ba số \({a^2},{b^2},{c^2}\) theo thứ tự cũng lập thành một cấp số cộng.
Tổng 20 số hạng đầu của một cấp số cộng với công sai bằng 3 là 650 . Tìm số hạng đầu của cấp số cộng này.
Tìm \(x\) để \(2x,3x + 2\) và \(5x + 3\) là các số hạng liên tiếp của một cấp số cộng.
Phải lấy tổng của bao nhiêu số hạng đầu của một cấp số cộng có số hạng đầu là 78 và công sai là \[ - 4\] để được tổng là 702?
Chuông đồng hồ ở một toà tháp đánh số tiếng đúng bằng số giờ và cứ mỗi 30 phút không phải là giờ đúng thì đánh 1 tiếng chuông. Hỏi bắt đầu từ lúc 1 giờ đêm đến 12 giờ trưa, chuông đồng hồ đó đã đánh tất cả bao nhiêu tiếng?
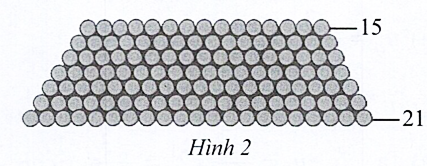
Các khúc gỗ được xếp như Hình 2. Lượt thứ nhất có 21 khúc, lượt thứ hai có 20 khúc, ..., lượt trên cùng có 15 khúc. Tính tổng số khúc gỗ đã được xếp.