Đề kiểm tra Các số đặc trưng đo xu thế trung tâm (có lời giải) - Đề 3
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cân nặng của \(40\) học sinh lớp \(10\) trường THPT A được cho bởi bảng sau

.
Tính số trung bình cộng của mẫu số liệu trên.
\(\bar x = 38,26\).
\(\bar x = 40,25\).
\(\bar x = 39,65\).
\(\bar x = 40,83\).
Kết quả điểm kiểm tra 15’ môn Toán của 100 em học sinh được trình bày ở bảng sau:
Điểm | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Cộng |
Tần số | 3 | 5 | 11 | 17 | 30 | 19 | 10 | 5 | 100 |
Số trung bình cộng của bảng phân bố tần số nói trên là
\(6,88\).
\(7,12\).
\(6,5\).
\(7,22\).
Một học sinh có điểm các bài kiểm tra Toán như sau: \(8;\,4;\,9;\,8;\,6;\,6;\,9;\,9;\,9\). Điểm trung bình môn Toán của học sinh đó (làm tròn đến \(1\) chữ số thập phân) là
\(7,3\).
\[6,8\].
\[8,5\].
\[7,6\].
Thống kê điểm kiểm tra môn Lịch Sử của 45 học sinh lớp 10A như sau:
Điểm | 5 | 6 | 7 | 8 | 9 | 10 |
Số học sinh | 2 | 11 | 9 | 16 | 4 | 3 |
Số trung vị trong điểm các bài kiểm tra đó là
\(8,1\)điểm.
\(7,4\) điểm.
\(7,5\) điểm.
\(8\) điểm.
Cho mẫu số liệu thống kê \(\left\{ {2;4;6;8;10} \right\}\). Số trung bình của mẫu số liệu trên là:
\(7\).
\(12\).
\(6.5\).
\(6\).
Thời gian chạy \(50m\) của \(20\) học sinh được ghi lại trong bảng dưới đây:
Thời gian (giây) | \(8,3\) | \(8,4\) | \(8,5\) | \(8,7\) | \(8,8\) |
Tần số | \(2\) | \(3\) | \(9\) | \(5\) | \(1\) |
Số trung bình cộng thời gian chạy của học sinh là
\(8,54\).
\(4\).
\(8,50\).
\(8,53\).
Cho mẫu số liệu \(10\), \(8\), \(6\), \(2\), \(4\). Số trung bình cộng của mẫu là
\(2,8\).
\(2,4\).
\(6\).
\(8\).
Mốt của một bảng phân bố tần số là
tần số lớn nhất trong bảng phân bố tần số.
giá trị có tần số lớn nhất trong bảng phân bố tần số.
giá trị có tần số nhỏ nhất trong bảng phân bố tần số.
tần số nhỏ nhất trong bảng phân bố tần số.
Cho bảng số liệu thống kê chiều cao của một nhóm học sinh như sau:

Số trung vị của bảng số liệu nói trên là
\(161\).
\(153\).
\(163\).
\(156\).
Cho bảng số liệu điểm bài kiểm tra môn toán của 20 học sinh

Tìm số trung vị của bảng số liệu trên.
\(8\).
\(7,5\).
\(7,3\).
\(7\).
Cho bảng phân bố tần số như sau:
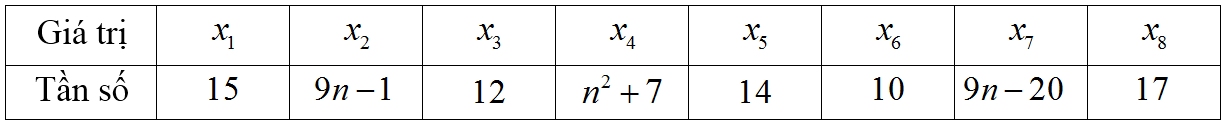
Tìm \(n\)để \(M_{_O}^{\left( 1 \right)} = {x_2}\,;\,M_{_O}^{\left( 2 \right)} = {x_4}\) là hai mốt của bảng số liệu trên.
\(n = 1\,;\,n = 8\).
\(n = 8\).
\(n = 1\).
\(n = 9\).
Điểm thi học kì của một học sinh như sau: \[4;\,6;\,2;\,7;\,3;\,5;\,9;\,8;\,7;\,10;\,9\]. Số trung bình và số trung vị lần lượt là
\(6,22\)và \(7\).
\(7\) và \(6\).
\(6,36\) và \(7\).
\(6\) và \(6\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho biết tình hình thu hoạch lúa vụ mùa năm 2022 của ba hợp tác xã ở một địa phương như sau:
Hợp tác xã | Năng suất lúa (tạ/ha) | Diện tích trồng lúa (ha) |
A | 40 | 150 |
B | 38 | 130 |
C | 36 | 120 |
Khi đó:
a) Sản lượng lúa của hợp tác xã A là: \(6000\) (tạ).
b) Sản lượng lúa của hợp tác xã B là: \(4950\) (tạ).
c) Sản lượng lúa của hợp tác xã C là: \(4120\) (tạ).
d) Năng suất lúa trung bình của toàn bộ ba hợp tác xã là: \(38,15\) (tạ/ha).
Số liệu sau đây cho ta lãi (quy tròn) hàng tháng của một cửa hàng trong năm 2022. Đơn vị: triệu đồng.
Tháng | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Lãi | 12 | 15 | 18 | 13 | 13 | 16 | 18 | 14 | 15 | 17 | 20 | 17 |
Khi đó:
a) Lãi thấp nhất của cửa hàng là \(13\)
b) Sắp xếp các số trong mẫu theo thứ tự không giảm:
\(\begin{array}{*{20}{l}}{12}&{13}&{13}&{14}&{15}&{15}&{16}&{17}&{17}&{18}&{18}&{20}\end{array}\)
c) Số trung bình của mẫu: \(\bar x \approx 13,67\) (triệu đồng).
d) Số trung vị là: \(16\).
Một cửa hàng vật liệu xây dựng thống kê số bao xi măng bán ra trong 23 ngày cuối năm 2004. Kết quả như sau: \(47;54;43;50;61;36;65;54;50;43;62;59\);\(36;45;45;33;53;67;21;45;50;36;58\).
Khi đó:
a) \(n = 22\)
b) Số trung bình là: \(\bar x \approx 42,39\).
c) 59 là số bao xi măng nhiều nhất được bán ra trong 23 ngày cuối năm 2004
d) Số trung vị là 50.
Có 100 học sinh tham dự kỳ thi học sinh giỏi Toán (thang điểm là 20) kết quả được cho bởi bảng sau.
Điểm | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
Tần số | 1 | 1 | 3 | 5 | 8 | 13 | 19 | 24 | 14 | 10 | 2 |
Khi đó:
a) Số trung bình là: \(\bar x \approx 15,23\).
b) Số liệu đứng thứ 50 là 16
c) Số trung vị là: \(15,5\).
d) Mốt của mẫu là 16.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Cho mẫu số liệu có bảng tần suất như sau:
Giá trị \({x_i}\) | 4 | 5 | 6 | 7 | 8 |
Tần số tương đối \({f_i}\) | 0,1 | 0,45 | 0,2 | 0,1 | 0,15 |
Ta có số trung bình của mẫu số liệu là:
Hãy tìm các tứ phân vị của mẫu số liệu sau: \(2;3;7;4;5;3;4;4\).
Trong 6 tháng đầu năm, số sản phẩm bán ra mỗi tháng của một cửa hàng đều tăng khoảng \(25\% \) so với tháng trước đó. Biết rằng, trong bảng dưới đây, số sản phẩm bán ra của một tháng bị nhập sai. Hãy tìm tháng đó.
Tháng | 1 | 2 | 3 | 4 | 5 | 6 |
Số sản phẩm bán ra | 145 | 180 | 225 | 279 | 390 | 435 |
Bảng sau thống kê số lớp và số học sinh theo từng khối ở một trường Trung học phổ thông.
Khối | 10 | 11 | 12 |
Số lớp | 14 | 13 | 15 |
Số học sinh | 555 | 519 | 615 |
Hiệu trưởng trường đó cho biết sĩ số mỗi lớp trong trường đều không vượt quá 40 học sinh. Biết rằng trong bảng trên có một khối lớp bị thống kê sai, hãy tìm khối lớp đó.
Trong giờ học Toán lớp 7, giáo viên giao nhiệm vụ cho mỗi nhóm đo các góc của một tam giác. Kết quả được ghi lại trong bảng sau:

Trong bảng trên có nhóm ghi kết quả sai. Hãy tìm nhóm nào sai?
Một tổ công nhân may gồm 5 người. Trong một ngày, mỗi người có thể may được từ 7 đến 10 sản phẩm. Cuối mỗi ngày, tổ trưởng thống kê lại số sản phẩm của cả tổ trong bảng sau:
Ngày | Ngày thứ nhất | Ngày thứ hai | Ngày thứ ba | Ngày thứ tư | Ngày thứ năm |
Số sản phẩm | 40 | 42 | 36 | 49 | 60 |
Tổ trưởng đã thống kê đúng chưa?






