Đề kiểm tra Các số đặc trưng đo xu thế trung tâm (có lời giải) - Đề 1
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Số áo bán được trong một quý ở cửa hàng bán áo sơ mi nam được thống kê như sau:
Cỡ áo | 36 | 37 | 38 | 39 | 40 | 41 | 42 |
Tần số (Số áo bán được) | 13 | 45 | 126 | 125 | 110 | 40 | 12 |
Giá trị mốt của bảng phân bố tần số trên bằng
\(38\).
\(126\).
\(42\).
\(12\).
Tiền lương hàng tháng của \[7\] nhân viên trong một công ty du lịch lần lượt là:\[6,5\]; \[8,4\]; \[6,9\]; \[7,2\]; \[2,5\]; \[6,7\]; \[3,0\] (đơn vị: triệu đồng). Số trung vị của dãy số liệu thống kê trên bằng
\(6,7\) triệu đồng.
\(7,2\) triệu đồng.
\(6,8\) triệu đồng.
\(6,9\) triệu đồng.
Điểm kiểm tra môn Toán cuối năm của một nhóm gồm 9 học sinh lớp 6 lần lượt là 1; 1; 3; 6; 7; 8; 8; 9; 10. Điểm trung bình của cả nhóm gần nhất với số nào dưới đây?
\(7,5\).
\(7\).
\(6,5\).
\(5,9\).
Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là
Mốt.
Số trung bình.
Số trung vị.
Độ lệch chuẩn.
Điểm kiểm tra của 24 học sinh được ghi lại trong bảng sau: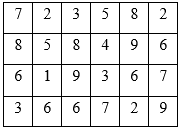
Tìm mốt của điểm điều tra.
\[2\].
\[7\].
\[6\].
\[9\].
Kết quả điểm kiểm tra 45 phút môn Hóa Học của 100 em học sinh được trình bày ở bảng sau:
Điểm | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Cộng |
Tần số | 3 | 5 | 14 | 14 | 30 | 22 | 7 | 5 | 100 |
Số trung bình cộng của bảng phân bố tần số nói trên là
\(6,82\).
\(4\).
\(6,5\).
\(7,22\).
Điều tra tiền lương một tháng của 100 người lao động trên địa bàn một xã ta có bảng phân bố tần số sau:
Tiền lương (VND) | 5.000.000 | 6.000.000 | 7.000.000 | 8.000.000 | 9.000.000 | 9.500.000 |
Tần số | 26 | 34 | 20 | 10 | 5 | 5 |
Tìm mốt của bảng phân bố tần số trên.
\(5.000.000\).
\(6.000.000\).
\(7.500.000\).
\(9.500.000\).
Cho bảng phân bố tần số sau: khối lượng \(20\) học sinh lớp \(10A\)
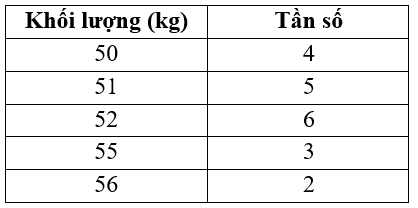
Số trung bình cộng \(\overline x \) của bảng số liệu đã cho là
\(\overline x = 53\).
\(\overline x = 52,8\).
\(\overline x = 52,2\).
\(\overline x = 52\).
Cho bảng số liệu thống kê chiều cao của một nhóm học sinh như sau:

Số trung vị dưới của bảng số liệu nói trên là
\(161\).
\(154\).
\(163\).
\(156\).
Cho bảng phân bố tần số như sau: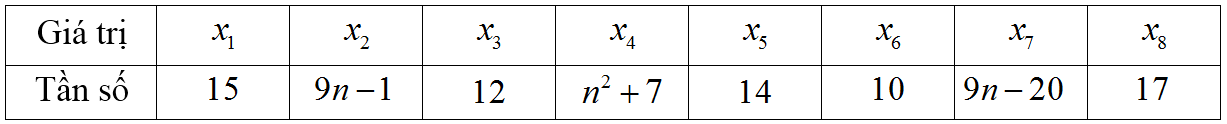
Tìm \(n\)để \(M_{_O}^{\left( 1 \right)} = {x_2}\,;\,M_{_O}^{\left( 2 \right)} = {x_4}\) là hai mốt của bảng số liệu trên.
\(n = 1\,;\,n = 8\).
\(n = 8\).
\(n = 1\).
\(n = 9\).
Nhiệt độ trung bình hàng tháng trong một năm được ghi lại trong bảng sau
Tháng | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) | \(9\) | \(10\) | \(11\) | 12 |
Nhiệt độ | \(16\) | \(20\) | \(25\) | \(28\) | \(30\) | \(30\) | \(28\) | \(25\) | \(25\) | \(20\) | \(18\) | \(16\) |
Mốt của dấu hiệu là
\(20\).
\(25\).
\(28\).
\(30\).
Cho bảng số liệu điểm kiểm tra môn Toán của 20 học sinh.
Điểm | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) | \(9\) | \(10\) | Cộng |
Số học sinh | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(4\) | \(1\) | \(20\) |
Số trung vị của bảng số liệu trên là
\(7\).
\(8\).
\(7,5\).
\(7,3\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Tập đoàn \(X\) có 24 công ty. Thống kê cuối năm cho biết doanh thu (đơn vị triệu đồng) của 24 công ty con như sau:
35432 | 14215 | 24436 | 13978 | 45713 | 16323 | 37488 | 13458 |
57754 | 53345 | 80234 | 117245 | 74506 | 86851 | 47678 | 611298 |
19397 | 48644 | 8324 | 9599 | 94338 | 45390 | 37492 | 811854 |
Khi đó:
a) Doanh thu thấp nhất là 9599
b) Doanh thu lớn nhất là 811854
c) Số trung bình của mẫu số liệu trên khoảng \(100208.\)
d) Số trung vị là 45551,5.
Thống kê chiều cao (đơn vị cm) của nhóm 15 bạn nam lớp 10 cho kết quả như sau:
162 | 157 | 170 |
| 165 | 166 | 157 | 159 | 164 | 172 | 155 | 156 | 156 | 180 | 165 | 155 |
Khi đó:
a) Chiều cao thấp nhất là 156
b) \({Q_2} = 162\)
c) \({Q_1} = 157\)
d) \({Q_3} = 170\)
Số giờ học thêm ngoài trường học của 30 học sinh được thống kê như sau:
2 | 2 | 1 | 3 | 5 | 6 | 5 | 7 | 6 | 6 | 7 | 8 | 7 | 7 | 6 |
6 | 7 | 6 | 4 | 6 | 0 | 8 | 6 | 7 | 0 | 0 | 4 | 6 | 8 | 7 |
Khi đó:
a) Số giờ học thêm ngoài trường học của 30 học sinh lớn nhất là 8
b) Số trung bình là 5,1.
c) \({Q_1} = 3\)
d) \({Q_2} = 6\)
Thống kê số bao xi măng được bán ra tại một cửa hàng vật liệu xây dựng trong 24 tháng cho kết quả như sau:
72 | 89 | 88 | 73 | 63 | 265 | 69 | 65 |
94 | 80 | 81 | 98 | 66 | 71 | 84 | 73 |
93 | 59 | 60 | 61 | 83 | 72 | 85 | 66 |
Khi đó:
a) Mỗi tháng cửa hàng bán trung bình 83,75 bao.
b) Số trung vị là: 72.
c) Sai khác giữa số trung bình và số trung vị là 10,75.
c) Khoảng cách từ \({Q_1}\) đến \({Q_2}\) là 8
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Bảng điểm kiểm tra học kì 1 môn Toán của lớp \(10\;A\) có 30 học sinh được cho như sau:
9 | 9 | 8,5 | 7 | 7 | 4 | 5 | 6 | 6 | 9 | 4 | 5 | 7,5 | 6,5 | 6 |
8,5 | 5 | 5 | 8 | 7 | 7 | 5 | 5 | 6 | 6 | 8 | 9 | 5 | 7 | 4 |
Tính điểm trung bình của lớp \(10\;A\).
Bài thi Tiếng Anh gồm có 100 câu trắc nghiệm, mỗi đáp án chọn đúng được 1 điểm, chọn sai 0 điểm. Kết quả kiểm tra của lớp \(10\;A\) được thống kê như sau:
54 | 67 | 87 | 23 | 54 | 76 | 15 | 64 | 74 | 35 | 65 | 60 | 62 | 50 | 46 |
58 | 61 | 49 | 49 | 58 | 59 | 59 | 79 | 82 | 100 | 95 | 64 | 55 | 38 | 72 |
Tính số trung vị của mẫu số liệu trên.
Thời gian (đơn vị giờ) dành cho hoạt động thể thao trong tuần của một số học sinh được thống kê như sau:
0 | 0 | 1 | 2 | 1 | 2 | 5 | 6 | 2 | 4 |
Tính mốt của mẫu số liệu trên.
Để đưa ra quyết định tập trung sản xuất sản phẩm thương mại, công ty \(X\) đưa ra 3 mẫu sản phẩm (được đóng chung vào một gói) thăm dò thị trường bằng việc tặng kèm với một sản phẩm đã được bày bán trong siêu thị. Thông tin thu lại là phiếu bình chọn cho sản phẩm yêu thích nhất của khách hàng. Có 1000 gói sản phẩm đã được đưa ra và cho kết quả:
Sản phẩm | Sản phẩm A | Sản phẩm B | Sản phẩm C |
Số bình chọn | 352 | 546 | 102 |
Tìm mốt của mẫu dữ liệu trên.
Có 404 học sinh tham gia kì thi khảo sát chất lượng môn Toán. Điểm khảo sát được tính theo thang điểm 10 và thống kê như sau:
Điểm số | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Số học sinh | 11 | 12 | 41 | 56 | 29 | 34 | 61 | 50 | 91 | 19 |
a) Tính điểm số trung bình.
b) Tính mốt của mẫu số liệu.
Một nhóm 11 học sinh tham gia một kì thi. Số điểm thi của 11 học sinh đó được sắp xếp từ thấp đến cao theo thang điểm 100 như sau: \(0;0;63\); \(65;69;70;72;78;81;85;89\).
a) Tìm điểm số trung bình của nhóm 11 học sinh này?
b) Tìm trung vị và mốt của mẫu số liêu đã cho?






