Đề kiểm tra Các số đặc trưng đo xu thế trung tâm (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Số \[a\] thoả mãn có \(75\% \) giá trị trong mẫu số liệu nhỏ hơn \[a\] và \(25\% \) giá trị trong mẫu số liệu lớn hơn \[a\] là
số trung bình.
trung vị.
tứ phân vị thứ nhất.
tứ phân vị thứ ba.
Tìm hiểu thời gian xem ti vi trong tuần trước của một số học sinh thu được kết quả sau:

Tính thời gian xem ti vi trung bình trong tuần trước của các bạn học sinh này.
\(8,4375\).
\(8,125\).
\[8,75\].
\[8,28125\].
Khi độ chênh lệch các số liệu trong mẫu quá lớn thì đại lượng nào thích hợp đại diện cho các số liệu trong mẫu.
Số trung bình.
Số trung vị.
Phương sai.
Độ lệch chuẩn.
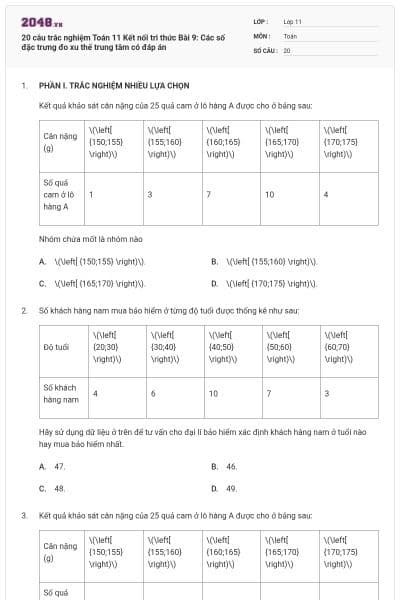
Điều tra \[42\] học sinh của một lớp \[11\] về số giờ tự học ở nhà, người ta có bảng sau đây:
Số trung vị của mẫu số liệu là.
\[4,25\].
\[3,75\].
\[4,75\].
\[3,25\].
Thống kê điểm học kì môn toán của các học sinh lớp 11A của một trường THPT, người ta thu được số liệu sau:
Tìm số trung vị của mẫu số liệu khi ta ghép lớp thành các nhóm có độ dài là \[1\] như sau:
\[\left[ {3\,;\,4} \right)\,,\,\left[ {4\,;\,5} \right)\,,...\,,\left[ {9\,;\,10} \right)\,\],.
\[6,7\].
\[9,3\].
\[5,8\].
\[5,7\].
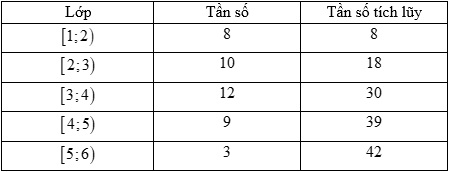
Điều tra \[42\] học sinh của một lớp \[11\] về số giờ tự học ở nhà, người ta có bảng sau đây: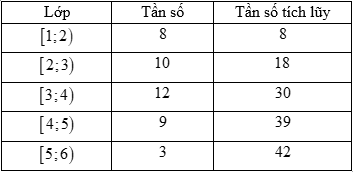
Nhận xét nào đúng về tứ phân vị của mẫu số liệu trên.
Tứ phân vị của mẫu số liệu trên luôn giảm.
Tứ phân vị của mẫu số liệu trên luôn tăng.
Tứ phân vị của mẫu số liệu trên luôn cách đều nhau.
Tứ phân vị của mẫu số liệu trên không tăng.
Thống kê điểm học kì môn toán của các học sinh lớp 11A của một trường THPT, người ta thu được số liệu sau:
Xác định tứ phân vị của mẫu số liệu khi ta ghép lớp thành các nhóm có độ dài là \[1\] như sau: \[\left[ {3\,;\,4} \right)\,,\,\left[ {4\,;\,5} \right)\,,...\,,\left[ {9\,;\,10} \right)\,\],.
\[4,6\,;\,5,7\,;\,7,3\].
\[4,6\,;\,5,7\,;\,7,4\].
\[5,6\,;\,6,7\,;\,8,3\].
\[4,7\,;\,5,7\,;\,7,4\].
Một của hàng bán 3 loại hoa quả nhập khẩu: Nho Mỹ, Lê Hàn Quốc và Táo New Zealand. Sau khi giảm giá mỗi loại lần lượt là \(x,\)\(y,\)\(z\) trên \(1kg\)thì số liệu tính toán được ghi lại bởi bảng sau:
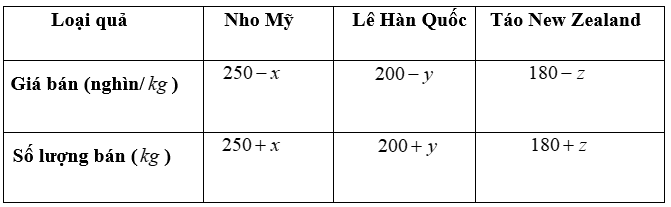
Biết rằng \(x + y + z = 120\). Tính giá trị \(x,\)\(y,\)\(z\) để lợi nhuận bình quân của \(1kg\)hoa quả đạt được cao nhất.
\[x = y = z = 40\].
\[x = 50\,;\,y = 30\,;\,z = 40\].
\[x = 30\,;\,y = 50\,;\,z = 40\].
\[x = 20\,;\,y = 60\,;\,z = 40\].
Cho dãy số liệu thống kê: \(50\,,\,48\,,\,34\,,\,36\,,\,56\,,\,35\,,\,43\,,\,38\,,\,55\). Số trung vị là
\[38\].
\[35\].
\[43\].
\[55\].
Thống kê điểm kiểm tra một tiết môn Toán của lớp 11A của trường THPT Nguyễn Huệ được ghi lại như sau:
Số trung vị của mẫu số liệu trên là
\[8,0\].
\[7,5\].
\[7,8\].
\[8,5\].
Thời gian đọc sách mỗi ngày của một số học sinh được cho trong bảng sau
Xác định trung vị của mẫu số liệu ghép nhóm.
\[25\].
\[26\].
\[25,56\].
\[26,67\].
Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốtcủamẫu số liệutrênlà
\[[40;60)\].
\[[20;40)\].
\[[60;80)\].
\[[80;100)\].
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Các mệnh đề sau đúng/sai
a) Giá trị đại diện của lớp \[\left[ {50;52} \right)\]là \[53\].
b) Tần số của lớp \[\left[ {58;60} \right)\]là \[95\].
c) Tần số của lớp \[\left[ {52;54} \right)\]là \[35\].
d) Số \[50\] không phụ thuộc lớp \[\left[ {54;56} \right)\]
Người ta đo đường kính của 61 cây gỗ được trồng sau 12 năm (đơn vị: centimét), họ thu được bảng tần số ghép nhóm sau:
Đường kính | \([20;25)\) | \([25;30)\) | \([30;35)\) | \([35;40)\) | \([40;45)\) |
Số cây | 4 | 12 | 26 | 13 | 6 |
a) Cỡ mẫu của mẫu số liệu là \(n = 61\).
b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} \approx 19,69\).
c) Tứ phân vị thứ hai của mẫu số liệu ghép nhóm là:\({Q_2} = 32,79\).
d) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 36,44.{\rm{ }}\)
Số điểm một cầu thủ ghi được trong 20 trận đấu được cho ở bảng sau:
25 | 23 | 21 | 13 | 8 | 14 | 15 | 18 | 22 | 11 |
24 | 12 | 14 | 14 | 18 | 6 | 8 | 25 | 10 | 11 |
a) Tứ phân vị thứ hai của dãy số liệu là: \({Q_2} = 14.{\rm{ }}\)
b) Tứ phân vị thứ ba của dãy số liệu là \({Q_3} = 11,5.{\rm{ }}\)
c) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:
Điểm số | \([6;10)\) | \([11;15)\) | \([16;20)\) | \([21;25)\) |
Số trận | 4 | 8 | 2 | 6 |
d) Ứớc lượng tứ phân vị của số liệu ở bảng tần số ghép nhóm trên ta được tứ phân vị thứ hai của mẫu số liệu là: \({Q_2} = 8,25\).
Cân nặng của một số lợn con mới sinh thuộc hai giống \(A\) và \(B\) được cho ở bảng đây (đơn vị: kg)
Cân nặng \((kg)\) | \([1,0;1,1)\) | \([1,1;1,2)\) | \([1,2;1,3)\) | \([1,3;1,4)\) |
Số con giống A | 8 | 28 | 32 | 17 |
Số con giống B | 13 | 14 | 24 | 14 |
a) Cân nặng trung bình của giống \(A\) là: \(1,22.{\rm{ }}\)
b) Cân nặng trung bình của giống \(B\) là: \(1,21.{\rm{ }}\)
c) Tứ phân vị thứ nhất của mẫu số liệu lợn con giống \(A\) là: \({Q_{1A}} = 1,15.{\rm{ }}\)
d) Tứ phân vị thứ nhất của mẫu số liệu lợn con giống \(B\) là: \({Q_{1B}} = 1,62.\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Quãng đường (km) các cầu thủ (không tính thủ môn) chạy trong một trận bóng đá tại giải ngoại hạng Anh được cho trong bảng thống kê sau:
Quãng đường | \([2;4)\) | \([4;6)\) | \([6;8)\) | \([8;10)\) | \([10;12)\) |
Số cầu thủ | 2 | 5 | 6 | 9 | 3 |
Tính quãng đường trung bình một cầu thủ chạy trong trận đấu này.
Thống kê số lần đi học muộn trong học kì của các bạn trong lớp, Nam thu được kết quả sau:
Số lần đi muộn | \(0 - 2\) | \(3 - 5\) | \(6 - 8\) | \(9 - 11\) | \(12 - 14\) |
Só học sinh | 23 | 8 | 5 | 3 | 1 |
Tính mốt của mẫu số liệu và giải thích ý nghĩa của giá trị thu được.
Trong các mẫu số liệu cho trong bài tập 3.23 và 3.24, ta có thể tìm mốt cho mẫu số liệu nào? Tìm mốt của mẫu số liệu đó và giải thích ý nghĩa của giá trị tìm được.
Bảng số liệu ghép nhóm sau cho biết chiều cao \((cm)\) của 50 học sinh lớp \(11A\).
Khoảng chiều cao (cm) | \([145;150)\) | \([150;155)\) | \([155;160)\) | \([160;165)\) | \([165;170)\) |
Số học sinh | 7 | 14 | 10 | 10 | 9 |
Tính mốt của mẫu số liệu ghép nhóm này. Có thể kết luận gì từ giá trị tính được?
Người ta thống kê tốc độ của một số xe ô tô di chuyển qua một trạm kiểm soát trên đường cao tốc trong một khoảng thời gian ở bảng sau:

Hãy ước lượng các tứ phân vị của mẫu số liệu ghép nhóm trên.
Cho mẫu số liệu ghép nhóm về chiều cao của 21 cây na giống.
Chiều cao \((cm)\) | \([0;5)\) | \([5;10)\) | \([10;15)\) | \([15;20)\) |
Số cây | 3 | 8 | 7 | 3 |
hãy cho biết tứ phân vị thứ nhất \({Q_1}\) và tứ phân vị thứ ba \({Q_3}\) thuộc nhóm nào.