Đề kiểm tra Các số đặc trưng đo xu thế trung tâm (có lời giải) - Đề 1
23 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Số \[a\] thoả mãn có \(25\% \) giá trị trong mẫu số liệu nhỏ hơn \[a\] và \(75\% \) giá trị trong mẫu số liệu lớn hơn \[a\] là
số trung bình.
trung vị.
tứ phân vị thứ nhất.
tứ phân vị thứ ba.
Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như sau.![]()
Nhóm chứa trung vị của mẫu số liệu là
\([2;3,5)\).
\([3,5;5)\).
\([5;6,5)\).
\([6,5;8)\).
Công việc nào sau đây không phụ thuộc vào các công việc của môn thống kê?
Thu thập số liệu.
Trình bày số liệu.
Phân tích và xử lí số liệu.
Ra quyết định dựa trên số liệu.
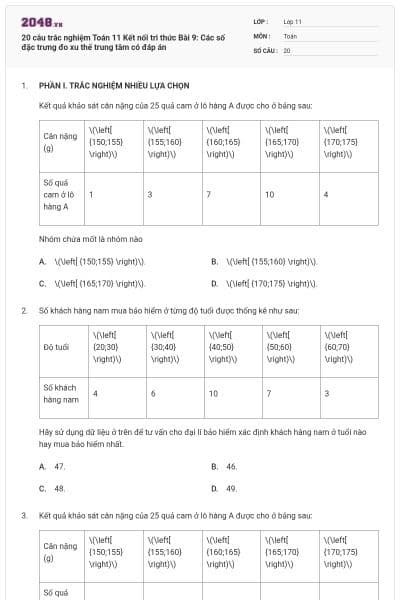
Điều tra về chiều cao của học sinh khối lớp 10, ta có kết quả sau: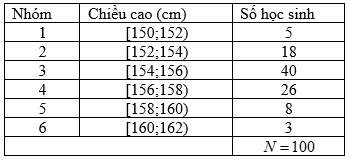
Giá trị đại diện của nhóm thứ tư là
\[156,5\].
\[157\].
\[157,5\].
\[158\].
Cho bảng phân bố tần số ghép lớp:
![]()
Mệnh đề đúng là:
Giá trị trung tâm của lớp \[\left[ {50;52} \right)\]là \[53\].
Tần số của lớp \[\left[ {58;60} \right)\] là \[95\]
Tần số của lớp \[\left[ {52;54} \right)\] là \[35\]
Số 50 không phụ thuộc lớp \[\left[ {54;56} \right)\]
Cho bảng phân bố tần số, tần suất ghép lớp chiều cao của các học sinh trong một lớp học như sau:
Tìm giá trị của \(a + 2b + 10c\).
\(225\).
\(158\).
\(255\).
\(202\).
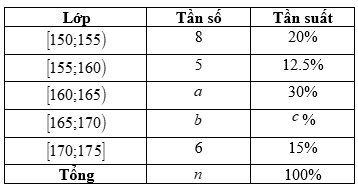
Điểm kiểm tra 15 phút của 36 học sinh lớp 11A được cho bởi bảng tần số ghép nhóm sau: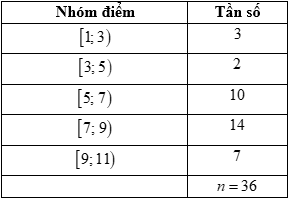
Mốt của bảng ghép lớp trên là giá trị nào sau?
\[7,73\].
\[6,12\].
\[5,09\].
\[7,03\].
Cho bảng mẫu số liệu ghép nhóm là chiều cao của học sinh lớp 5 tuổi
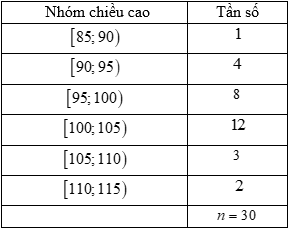
Số liệu và nhóm của bảng trên là
\[30\]và \[5\].
\[115\]và \[30\].
\[115\]và \[6\].
\[30\]và \[6\].
Cho bảng mẫu số liệu ghép nhóm là chiều cao của học sinh lớp 5 tuổi![Cho bảng mẫu số liệu ghép nhóm là chiều cao của học sinh lớp 5 tuổi Tìm \(x\) biết tần số tích lũy của nhóm \(3\) là \(23\) A. \[5\]. B. \[3\]. C. \[8\]. D. \[10\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/19-1759665732.png)
Tìm \(x\) biết tần số tích lũy của nhóm \(3\) là \(23\)
\[5\].
\[3\].
\[8\].
\[10\].
Điểm trung bình các môn học kì I của bạn An được cho bởi bảng sau:
![Điểm trung bình các môn học kì I của bạn An được cho bởi bảng sau: Tính điểm trung bình môn học kì I của bạn An. A. \[8,0\]. B. \[8,375\]. C. \[8,2\]. D. \[8,5\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/20-1759665777.png)
Tính điểm trung bình môn học kì I của bạn An.
\[8,0\].
\[8,375\].
\[8,2\].
\[8,5\].
Tìm cân nặng trung bình của học sinh lớp 11D cho trong bảng sau, làm tròn đến hàng phần trăm.
\[51,8\].
\[51,81\].
\[52\].
\[51,809\].
Thời gian luyện tập trong một ngày (tính theo giờ) của một số vận động viên được ghi lại ở bảng sau:
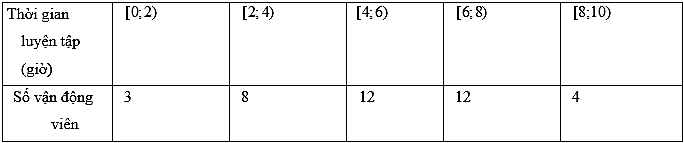
Hãy xác định các tứ phân vị thứ 3 của mẫu số liệu trong
3,6875.
5,417.
7,042.
7,68.
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho bảng tần số ghép nhóm số liệu thống kê cân nặng của 40 học sinh lớp 11 A trong một trường trung học phổ thông (đơn vị: kilôgam).
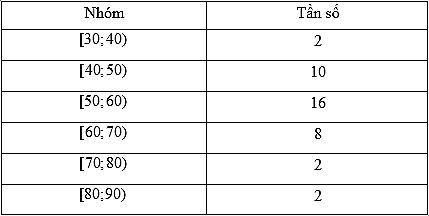
Hãy ước lượng các tứ phân vị của mẫu số liệu ghép số trên, Các mệnh đề sau đúng/sai
a) \({Q_1} = 49(\;kg);{Q_2} = 50(\;kg);{Q_3} = 52,5(\;kg)\).
b) \({Q_1} = 48(\;kg);{Q_2} = 55(\;kg);{Q_3} = 62,5(\;kg)\).
c) \({Q_1} = 47(\;kg);{Q_2} = 54(\;kg);{Q_3} = 63,5(\;kg)\).
d) \({Q_1} = 46(\;kg);{Q_2} = 53(\;kg);{Q_3} = 64,5(\;kg)\).
Dựa vào bảng tần số mẫu số liệu ghép nhóm sau, hãy tìm tứ phân vị của nó.
Nhóm | \([30;40)\) | \([40;50)\) | \([50;60)\) | \([60;70)\) | \([70;80)\) | \([80;90)\) |
Tần số | 2 | 10 | 16 | 8 | 2 | 2 |
a) Cỡ mẫu của mẫu số liệu là \(n = 40\).
b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 48\)
c) Tứ phân vị thứ hai của mẫu số liệu ghép nhóm là:\({Q_2} = 45\)
d) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \[{Q_3} = 61,5\]
Một hãng xe ô tô thống kê lại số lần gặp sự cố về động cơ của 100 chiếc xe cùng loại sau 2 năm sử dụng đầu tiên ở bảng sau:
Số lần gặp sự cố | \([1;2]\) | \([3;4]\) | \([5;6]\) | \([7;8]\) | \([9;10]\) |
Số xe | 17 | 33 | 25 | 20 | 5 |
a) Cỡ mẫu của mẫu số liệu là \(n = 100\).
b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} \approx 1,98\).
c) Tứ phân vị thứ hai của mẫu số liệu ghép nhóm là:\({Q_2} = 4,5.{\rm{ }}\)
d) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 6,5.{\rm{ }}\)
Một hãng xe ô tô thống kê lại số lần gặp sự cố về động cơ của 100 chiếc xe cùng loại sau 2 năm sử dụng đầu tiên ở bảng sau:
Số lần gặp sự cố | \([1;2]\) | \([3;4]\) | \([5;6]\) | \([7;8]\) | \([9;10]\) |
Số xe | 17 | 33 | 25 | 20 | 5 |
a) Cỡ mẫu của mẫu số liệu là \(n = 100\).
b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} \approx 1,98\).
c) Tứ phân vị thứ hai của mẫu số liệu ghép nhóm là:\({Q_2} = 4,5.{\rm{ }}\)
d) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 6,5.{\rm{ }}\)
Hãy tìm các tứ phân vị của mẫu số liệu được cho dưới dạng bảng tần số ghép nhóm sau:
Nhóm | \([0;2)\) | \([2;4)\) | \([4;6)\) | \([6;8)\) | \([8;10)\) |
Tần số | 3 | 8 | 12 | 12 | 4 |
a) Cỡ mẫu của mẫu số liệu là \(n = 38\).
b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} \approx 2,69\).
c) Tứ phân vị thứ hai của mẫu số liệu ghép nhóm là:\({Q_2} \approx 5,42.{\rm{ }}\)
d) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 7,04\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một trang báo điện tử thống kê thời gian người sử dụng đọc thông tin trên trang trong mỗi lần truy cập ở bảng sau:

Hãy ước lượng các tứ phân vị của mẫu số liệu ghép nhóm trên.
Tìm hiểu thời gian xem ti vi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau:
Thời gian (giờ) | \([0;5)\) | \([5;10)\) | \([10;15)\) | \([15;20)\) | \([20;25)\) |
Số học sinh | 8 | 16 | 4 | 2 | 2 |
Tính thời gian xem ti vi trung bình trong tuần trước của các bạn học sinh này.
Thời gian (phút) để học sinh hoàn thành một câu hỏi thi được cho như sau:
Thời gian (phút) | \([0,5;10,5)\) | \([10,5;20,5)\) | \([20,5;30,5)\) | \([30,5;40,5)\) | \([40,5;50,5)\) |
Số học sinh | 2 | 10 | 6 | 4 | 3 |
Tìm mốt của mẫu số liệu ghép nhóm này.
Mức thưởng tết (triệu đồng) mà các công nhân một nhà máy nhận được như sau:
Mức thưởng | \([5;10)\) | \([10;15)\) | \([15;20)\) | \([20;25]\) |
Só công nhân | 13 | 35 | 47 | 25 |
Tìm mốt của mẫu số liệu ghép nhóm. Cho biết ý nghĩa của giá trị thu được.
Cho mẫu số liệu ghép nhóm về chiều cao của 21 cây na giống.
Chiều cao \((cm)\) | \([0;5)\) | \([5;10)\) | \([10;15)\) | \([15;20)\) |
Số cây | 3 | 8 | 7 | 3 |
Gọi \({x_1},{x_2}, \ldots ,{x_{21}}\) là chiều cao của các cây giống, đã được sắp xếp theo thứ tự tăng dần. Khi đó, \({x_1}, \ldots ,{x_3}\) thuộc \([0;5),{x_4}, \ldots ,{x_{11}}\) thuộc \([5;10), \ldots \) Hỏi trung vị thuộc nhóm nào?
Ghi lại tốc độ bóng trong 200 lần giao bóng của một vận động viên môn quần vợt cho kết quả như bảng bên.
Tốc độ \(v(\;km/h)\) | Số lần |
\(150 \le v < 155\) | 18 |
\(155 \le v < 160\) | 28 |
\(160 \le v < 165\) | 35 |
\(165 \le v < 170\) | 43 |
\(170 \le v < 175\) | 41 |
\(175 \le v < 180\) | 35 |
Tính trung vị của mẫu số liệu ghép nhóm này.