Đề kiểm tra Bất phương trình bậc nhất hai ẩn (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Câu nào sau đây sai?.
Miền nghiệm của bất phương trình \(x + 3 + 2\left( {2y + 5} \right) < 2\left( {1 - x} \right)\) là nửa mặt phẳng chứa điểm
\(\left( { - 3; - 4} \right)\).
\(\left( { - 2; - 5} \right)\).
\(\left( { - 1; - 6} \right)\).
\(\left( {0;0} \right)\).
Câu nào sau đây đúng?.Miền nghiệm của bất phương trình \(4\left( {x - 1} \right) + 5\left( {y - 3} \right) > 2x - 9\) là nửa mặt phẳng chứa điểm
\(\left( {0;0} \right)\).
\(\left( {1;1} \right)\).
\(\left( { - 1;1} \right)\).
\(\left( {2;5} \right)\).
Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình \[2x + y < 1\]?
\[\left( { - 2;1} \right)\].
\[\left( {3; - 7} \right)\].
\[\left( {0;1} \right)\].
\[\left( {0;0} \right)\].
Miền nghiệm của bất phương trình\[3x + 2\left( {y + 3} \right) > 4\left( {x + 1} \right) - y + 3\] là phần mặt phẳng chứa điểm nào?
\[\left( {3;0} \right)\].
\[\left( {3;1} \right)\].
\[\left( {1;1} \right)\].
\[\left( {0;0} \right)\].
Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
\(2x - 5y + 3z \le 0\).
\(3{x^2} + 2x - 4 > 0\).
\(2{x^2} + 5y > 3\).
\(2x + 3y < 5\).
Điểm nào sau đây thuộc miền nghiệm của bất phương trình \[2x + y - 3 > 0\]?
\[Q\left( { - 1; - 3} \right)\].
\[M\left( {1;\frac{3}{2}} \right)\].
\[N\left( {1;1} \right)\].
\[P\left( { - 1;\frac{3}{2}} \right)\].
Miền nghiệm của bất phương trình \[\left( {1 + \sqrt 3 } \right)x - \left( {1 - \sqrt 3 } \right)y \ge 2\] chứa điểm nào sau đây?
\(A\left( {1\,\,;\,\, - 1} \right)\).
\(B\left( { - 1\,\,;\,\, - 1} \right)\).
\(C\left( { - 1\,\,;\,\,1} \right)\).
\(D\left( { - \sqrt 3 \,\,;\,\,\sqrt 3 } \right)\).
Miền nghiệm của bất phương trình \[5\left( {x + 2} \right) - 9 < 2x - 2y + 7\;\;\] là phần mặt phẳng không chứa điểm nào?
\[\left( { - 2;1} \right)\].
\[\left( {2;3} \right)\].
\[\left( {2; - 1} \right)\].
\[\left( {0;0} \right)\].
Miền nghiệm của bất phương trình \[x - 2 + 2\left( {y - 1} \right) > 2x + 4\] chứa điểm nào sau đây?
\(A\left( {1\,\,;\,\,1} \right).\)
\(B\left( {1\,\,;\,\,5} \right).\)
\(C\left( {4\,\,;\,\,3} \right).\)
\(D\left( {0\,\,;\,\,4} \right).\)
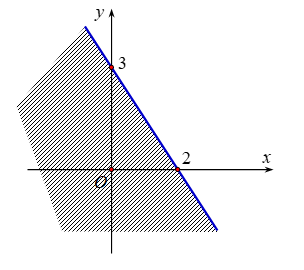
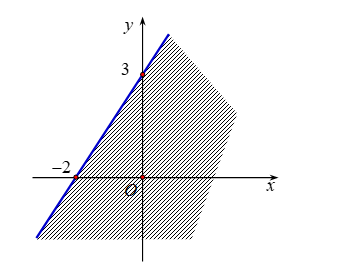
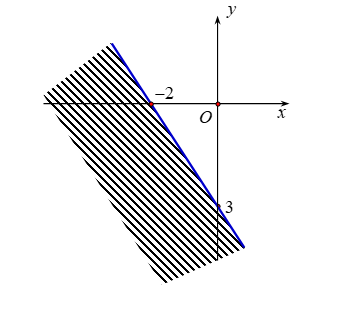
Miền nghiệm của bất phương trình \(3x - 2y > - 6\) là
C. 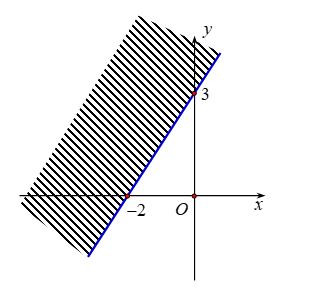
Miền nghiệm của bất phương trình \(3x + 2y > 6\) là
A. 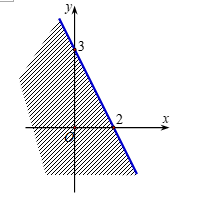
B. 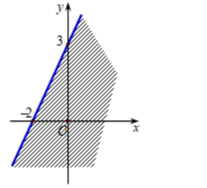
C. 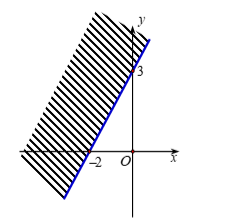
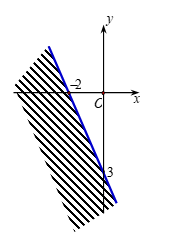
Cặp số \(\left( {{x_0};{y_0}} \right)\) nào là nghiệm của bất phương trình \(3x - 3y \ge 4\).
\(\left( {{x_0};{y_0}} \right) = \left( { - 2;2} \right)\).
\(\left( {{x_0};{y_0}} \right) = \left( {5;1} \right)\).
\(\left( {{x_0};{y_0}} \right) = \left( { - 4;0} \right)\).
\(\left( {{x_0};{y_0}} \right) = \left( {2;1} \right)\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho bất phương trình \( - 2x + 3y > 3\). Khi đó:
a) \((0;0)\) không là nghiệm bất phương trình.
b) \(( - 1;1)\) không là nghiệm bất phương trình.
c) \((0;1)\) không là nghiệm bất phương trình.
d) \((1;3)\) là nghiệm bất phương trình.
Điểm \(O(0;0)\) thuộc miền nghiệm của bất phương trình
a) ;
b) \(x + y + 2 \le 0\);
c) \(2x + 5y - 2 < 0\);
d) \(2x + y < 0\).
An thích ăn hai loại trái cây là cam và xoài, mỗi tuần mẹ cho An 200000 đồng để mua trái cây. Biết rằng giá cam là 15000 đồng/ 1 kg, giá xoài là 30000 đồng/1 kg. Gọi \(x,y\) lần lượt là số ki-lô-gam cam và xoài mà An có thể mua về sử dụng trong một tuần. Khi đó:
a) Trong tuần, số tiền An có thể mua cam là \(15000x\), số tiền An có thể mua xoài là \(30000y(x,y > 0)\).
b) Bất phương trình bậc nhất cho hai ẩn \(x,y\) là \(3x + 6y \ge 40\)
c) Cặp số \((5;4)\) thỏa mãn bất phương trình bậc nhất cho hai ẩn \(x,y\)
d) An có thể mua \(4kg\) cam, \(5\;kg\) xoài trong tuần.
Một công ty viễn thông tính phí 1 nghìn đồng mỗi phút gọi nội mạng và 2 nghìn đồng mỗi phút gọi ngoại mạng. Gọi \(x\) và \(y\) lần lượt là số phút gọi nội mạng, ngoại mạng của Bình trong một tháng và Bình muốn số tiền phải trả cho tồng đài luôn thấp hơn 100 nghìn đồng. Khi đó:
a) Số tiền phải trả cho cuộc gọi nội mạng mỗi tháng là \(x\) (nghìn đồng), số tiền phải trả cho cuộc gọi ngoại mạng mỗi tháng là \(2y\) (nghìn đồng). Điều kiện: \(x \in \mathbb{N},y \in \mathbb{N}\).
b) Bất phương trình bậc nhất gồm hai ẩn số \(x,y\) đã cho là \[x + 2y < 100\].
c) \(x = 50,y = 20\) nghiệm của bất phương trình bậc nhất gồm hai ẩn số \(x,y\) đã cho.
d) Miền nghiệm của bất phương trình bậc nhất gồm hai ẩn số \(x,y\) đã cho là một hình vuông
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Một hộ nông dân định trồng dứa và củ đậu trên diện tích 8 ha. Trên diện tích mỗi ha, nếu trồng dứa thì cần 20 công và thu 3 triệu đồng, nếu trồng củ đậu thì cần 30 công và thu 4 triệu đồng. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu ha để thu được nhiều tiền nhất, biết rằng tổng số công không quá 180 .
Có ba nhóm máy X,Y,Z dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm mỗi loại lần lượt phải dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được dùng cho trong bảng sau:
Nhóm
| Số máy trong mỗi nhóm | Số máy trong từng nhóm để sản xuất ra một đơn vị | |
Loại I | Loại II | ||
\(X\) | 10 | 2 | 2 |
Y | 4 | 0 | 2 |
\(Z\) | 12 | 2 | 4 |
Một đơn vị sản phẩm loại I lãi 3 nghìn đồng, một đơn vị sản phẩm loại II lãi 5 nghìn đồng. Hãy lập kế hoạch sản xuất đề cho tổng số tiền lãi thu được là cao nhất.
Tìm GTLN của \(f\left( {x,y} \right) = x + 2y\) với điều kiện \(\left\{ \begin{array}{l}0 \le y \le 4 & \left( {{d_1}} \right)\\0 \le x & & \left( {{d_2}} \right)\\x - y - 1 \le 0 & \left( {{d_3}} \right)\\x + 2y - 10 \le 0 & \left( {{d_4}} \right)\end{array} \right.\)
Bác Năm dự định trồng ngô và đậu xanh trên một mảnh đất có diện tích 8 hecta (ha). Nếu trồng 1 ha ngô thì cần 20 ngày công và thu được 40 triệu đồng. Nếu trồng 1 ha đậu xanh thì cần 30 ngày công và thu được 50 triệu đồng. Bác Năm cần trồng bao nhiêu ha cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng không quá 180 ngày công cho việc trồng ngô và đậu xanh.
Một công ty \(X\) có 2 phân xưởng \(A,B\) cùng sản xuất 2 loại sản phẩm \(M,N\). Số đơn vị sản phẩm các loại được sản xuất ra và chi phí mỗi giờ hoạt động của \(A,B\) như sau:
| Phân xưởng 1 | Phân xưởng 2 |
Sản phẩm \(M\) | 250 | 250 |
Sản phâm \(N\) | 100 | 200 |
Chi phí | \(600.000\) | \(1.000.000\) |
Công ty nhận được yêu cầu đặt hàng là 5000 đơn vị sản phẩm \(M\) và 3000 đơn vị sản phẩm \(N\).
Công ty đã tìm được cách phân phối thời gian cho mỗi phân xưởng hoạt động thỏa mãn yêu cầu đơn đặt hàng và chi phí thấp nhất. Hỏi chi phí thấp nhất bằng bao nhiêu?
Một người dùng ba loại nguyên liệu \(A,B,C\) để sản xuất ra hai loại sản phẩm \(P\) và \(Q\). Để sản xuất \(1\;kg\) mỗi loại sản phẩm \(P\) hoặc \(Q\) phải dùng một số kilôgam nguyên liệu khác nhau. Tổng số kilôgam nguyên liệu mỗi loại mà người đó có và số kilôgam từng loại nguyên liệu cần thiết để sản xuất ra 1 kg sản phẩm mỗi loại được cho trong bảng sau:
Loại nguyên liệu | Số kilôgam nguyên liệu đang có
| Số kilôgam từng loại nguyên liệu cần để sản xuất \(1{\bf{kg}}\) sản phẩm |
|
P | Q | ||
A | 10 | 2 | 2 |
B | 4 | 0 | 2 |
C | 12 | 2 | 4 |
Biết \(1\;kg\) sản phẩm \(P\) có lợi nhuận 3 triệu đồng và \(1\;kg\) sản phẩm \(Q\) có lợi nhuận 5 triệu đồng. Người đó đã lập được phương án sản xuất hai loại sản phẩm trên sao cho có lãi cao nhất. Hỏi lãi cao nhất bằng bao nhiêu?