20 câu trắc nghiệm Toán 10 Kết nối tri thức Bài 3. Bất phương trình bậc nhất hai ẩn (Đúng sai - trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
Cặp số nào sau đây không là nghiệm của bất phương trình \[2x + y - 7 > 0\].
\(\left( {3;2} \right)\).
\(\left( {5; - 1} \right)\).
\(\left( {4;0} \right)\).
\(\left( { - 2;5} \right)\).
Cặp số \[\left( {x;y} \right) = \left( {19;8} \right)\] là một nghiệm của bất phương trình nào sau đây?
\[2x - 5y--1 > 0\].
\[x--y < 0\].
\(3x - y - 5 < 0\).
\[x - 2y + 1 \ge 0\].
Điểm \(A\left( { - 1;3} \right)\) là điểm không thuộc miền nghiệm của bất phương trình nào sau đây?
\( - 3x + 2y - 4 < 0\).
\(x + 3y > 0\).
\(3x - y \le 0\).
\(2x - y + 4 < 0.\)
Cặp số nào sau đây là nghiệm của bất phương trình \[2x - y < 0\]?
\(\left( {0; - 1} \right)\).
\(\left( {3;5} \right)\).
\(\left( {1;4} \right)\).
\(\left( {2; - 1} \right)\).
Tìm \(m\) để bất phương trình \(mx - 3y < 2\) là bất phương trình bậc nhất hai ẩn?
\(m \in \mathbb{R}\).
\(m \ne 0\).
\(m > 0\).
\(m < 0\).
Điểm nào sau đây thuộc miền nghiệm của bất phương trình \[2x + y - 3 > 0\]?
\[Q\left( { - 1; - 3} \right)\].
\[M\left( {1;\frac{3}{2}} \right)\].
\[N\left( {1;1} \right)\].
\[P\left( { - 1;\frac{3}{2}} \right)\].
Phần không bị gạch chéo trong hình vẽ bên dưới là miền nghiệm của bất phương trình nào? 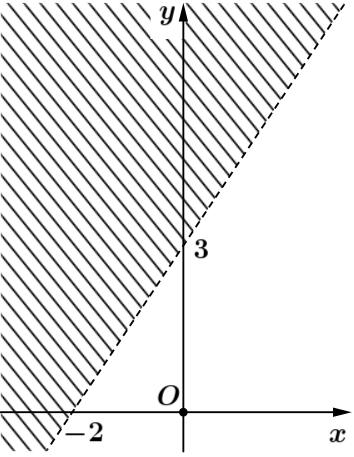
\(3x - 2y < - 6\).
\(3x - 2y > - 6\).
\(3x - 2y > 0\).
\(3x - 2y < 0\).
Miền nghiệm của bất phương trình \[\left( {1 + \sqrt 3 } \right)x - \left( {1 - \sqrt 3 } \right)y \ge 2\] chứa điểm nào sau đây?
\(A\left( {1\,\,;\,\, - 1} \right)\).
\(B\left( { - 1\,\,;\,\, - 1} \right)\).
\(C\left( { - 1\,\,;\,\,1} \right)\).
\(D\left( { - \sqrt 3 \,\,;\,\,\sqrt 3 } \right)\).
Tìm tất cả giá trị của tham số \(m\) để điểm \(M\left( {1;2} \right)\) thuộc miền nghiệm của bất phương trình bậc nhất hai ẩn \(\left( {m + 1} \right)x + \left( {{m^2} + m} \right)y - 1 > 0\).
\(m \in \left( {0; + \infty } \right)\).
\(m \in \left( { - \infty ; - \frac{3}{2}} \right)\).
\(m \in \left( { - \infty ; - \frac{3}{2}} \right) \cup \left( {0; + \infty } \right)\).
\(m \in \left( { - \frac{3}{2};0} \right)\backslash \left\{ { - 1} \right\}\).
Bạn Lan có 15 nghìn đồng để đi mua vở. Vở loại \(A\) có giá \(3000\) đồng một cuốn, vở loại \(B\) có giá \(4000\) đồng một cuốn. Hỏi bạn Lan có thể mua nhiều nhất bao nhiêu quyển vở sao cho bạn có cả hai loại vở?
\[3\].
\[5\].
\[4\].
\(6\).
Phần II. Trắc nghiệm đúng, sai
An thích ăn hai loại trái cây là cam và xoài, mỗi tuần mẹ cho An 200000 đồng để mua trái cây. Biết rằng giá cam là 15000 đồng/ 1 kg, giá xoài là 30000 đồng/1 kg. Gọi \(x,y\) lần lượt là số kilogam cam và xoài mà An có thể mua về sử dụng trong một tuần.
a) Trong tuần, số tiền An có thể mua cam là \(15000x\) đồng, số tiền An có thể mua xoài là \(30000y\) đồng với \(\left( {x,y > 0} \right)\).
b) Bất phương trình bậc nhất cho hai ẩn \(x,y\) là \(3x + 6y \ge 40\).
c) Cặp số \(\left( {5;4} \right)\) thỏa mãn bất phương trình bậc nhất cho hai ẩn \(x,y\).
d) An có thể mua \(4\)kg cam, \(5\;\)kg xoài trong tuần.
Một đội sản xuất cần 3 giờ để làm xong sản phẩm loại \(I\) và 2 giờ để làm xong sản phẩm loại II. Biết thời gian tối đa cho việc sản xuất hai sản phẩm trên là 18 giờ. Gọi \(x,y\) lần lượt là số sản phẩm loại \(I\), loại \(II\) mà đội làm được trong thời gian cho phép.
a) Tổng thời gian làm xong sản phẩm loại \(I\) là \(2x\), tổng thời gian làm xong sản phẩm loại II là \(3y\).
b) Bất phương trình bậc nhất hai ẩn theo \(x,y\) với điều kiện \(x,y \in \mathbb{N}\) là \(3x + 2y < 18\).
c) \(\left( {3\,;\,4} \right)\) là một nghiệm của bất phương trình bậc nhất hai ẩn theo \(x,y\) với điều kiện \(x,y \in \mathbb{N}\).
d) \(\left( {4;\,3} \right)\) là một nghiệm của bất phương trình bậc nhất hai ẩn theo \(x,y\) với điều kiện \(x,y \in \mathbb{N}\).
Một trò chơi chọn ô chữ đơn giản mà kết quả gồm một trong hai khả năng: Nếu người chơi chọn được chữ \(A\) thì người ấy được cộng 3 điểm, nếu người chơi chọn được chữ \(B\) thì người ấy bị trừ 1 điểm. Người chơi chỉ chiến thắng khi đạt được số điểm tối thiểu là 20. Gọi \(x,y\) theo thứ tự là số lần người chơi chọn được chữ \(A\) và chữ \(B\).
a) Tổng số điểm người chơi đạt được khi chọn chữ \(A\) là \(3x\), tổng số điểm người chơi bị trừ khi chọn chữ \(B\) là \(y\).
b) Bất phương trình bậc nhất hai ẩn \(x,y\) trong tình huống người chơi chiến thắng là \(3x - y \ge 18\)
c) Người chơi chọn được chữ \(A\) 7 lần và chọn được chữ \(B\) 1 lần thì người đó vừa đủ điểm dành chiến thắng trò chơi.
d) Người chơi chọn được chữ \(A\) 8 lần và chọn được chữ \(B\) 3 lần thì người đó vừa đủ điểm dành chiến thắng trò chơi.
Một công ty viễn thông tính phí 1 nghìn đồng mỗi phút gọi nội mạng và 2 nghìn đồng mỗi phút gọi ngoại mạng. Gọi \(x\) và \(y\) lần lượt là số phút gọi nội mạng, ngoại mạng của Bình trong một tháng. Bình muốn số tiền phải trả cho tồng đài luôn thấp hơn 100 nghìn đồng.
a) Số tiền phải trả cho cuộc gọi nội mạng mỗi tháng là \(x\) (nghìn đồng), số tiền phải trả cho cuộc gọi ngoại mạng mỗi tháng là \(2y\) (nghìn đồng) với điều kiện: \(x \in \mathbb{N},y \in \mathbb{N}\).
b) Bất phương trình bậc nhất gồm hai ẩn số \(x,y\) đã cho là \[x + 2y < 100\].
c) \(x = 50,y = 20\) nghiệm của bất phương trình bậc nhất gồm hai ẩn số \(x,y\) đã cho.
d) Miền nghiệm của bất phương trình bậc nhất gồm hai ẩn số \(x,y\) đã cho là một hình vuông.
Nhân ngày Quốc tế Thiếu nhi ngày 01 tháng 06, một rạp chiếu phim phục vụ các khán giả một bộ phim hoạt hình. Vé được bán ra có hai loại:

Loại 1 (dành cho trẻ từ 6 từ 13 tuổi): \(50.000\)đồng/vé
Loại 2 (dành cho người trên 13 tuổi): \(100.000\) đồng/vé
Người ta tính toán rằng, để không phải bù lỗ thì số tiền vé thu được ở rạp chiếu phim này phải đạt tối thiểu 20 triệu đồng. Gọi \(x\) là số lượng vé loại 1 bán được \(\left( {x \in \mathbb{N}} \right)\) và \(y\) là số lượng vé loại 2 bán được \(\left( {y \in \mathbb{N}} \right)\) .
a) Người ta sẽ phải bù lỗ trong trường hợp số tiền bán vé thoả mãn bất phương trình \(x + 2y < 400\).
b) Nếu bán được 250 vé loại 1 và 150 vé loại 2 thì rạp chiếu phim có lãi.
c) Nếu bán được 200 vé loại 1 và 100 vé loại 2 thì rạp chiếu phim hoà vốn.
d) Nếu bán được 50 vé loại 1 và 100 vé loại 2 thì rạp chiếu phim phải bù lỗ.
Phần III. Trắc nghiệm trả lời ngắn
Cho bất phương trình \(2x + 3y - 10 \le 0\). Hỏi có bao nhiêu cặp số nguyên \(\left( {{m_0}\,;\,{n_0}} \right)\) thoả mãn \(\left( {m_0^2\,;\,n_0^2} \right)\) là nghiệm của bất phương trình đã cho?
Một cửa hàng có kế hoạch nhập về \(110\) chiếc xe mô tô gồm hai loại \(A\) và \(B\) để bán. Mỗi chiếc xe loại \(A\) có giá \(30\) triệu đồng và mỗi chiếc xe loại \(B\) có giá \(50\) triệu đồng. Để số tiền dùng để nhập xe không quá 4 tỉ đồng thì của hàng cần nhập \(m\) chiếc xe loại \(A\) và \(n\) chiếc xe loại \(B\). Khi đó \(m + n\) bằng bao nhiêu?
Bạn Lan mang 150000 đồng đi nhà sách để mua một số quyển tập và bút. Biết rằng giá một quyển tập là 8000 đồng và giá của một cây bút là 6000 đồng. Bạn Lan có thể mua được tối đa bao nhiêu quyển tập nếu bạn đã mua 10 cây bút.
Bạn Việt mang \(100\,000\) đồng ra chợ mua hoa cúc và hoa hồng. Một bông hoa cúc có giá \(3\,000\) đồng, một bông hoa hồng có giá \(6\,000\) đồng. Gọi \(x\) và \(y\) lần lượt là số bông hoa cúc và số bông hoa hồng bạn Việt mua. Bất phương trình bậc nhất hai ẩn \(x,\,\,y\) để biểu diễn số tiền Việt mua hoa cúc và hoa hồng có dạng \(ax + 6y \le b\) với \(a,\,b \in \mathbb{N}\). Tính giá trị biểu thức \(T = a + b\).
Một cửa hàng bán hai loại đồ uống có tên là “Giọt lệ thiên thần” và “Giọt lệ ác quỷ”. Bốn ly “Giọt lệ thiên thần” có giá \(600\,000\) đồng, ba ly “Giọt lệ ác quỷ” có giá \(540\,000\)đồng. Hàng tháng, cửa hàng này phải chi trả \(6\,000\,000\) đồng tiền thuê nhân viên, \(8\,000\,000\) đồng tiền thuê mặt bằng, \(3\,000\,000\) đồng tiền nguyên liệu. (Ngoài ra cửa hàng không tốn thêm bất kỳ chi phí gì và thu nhập của cửa hàng chỉ đến từ việc bán hai loại đồ uống trên). Gọi \[x\] và \(y\) lần lượt là số ly “Giọt lệ thiên thần” và “Giọt lệ ác quỷ” mà cửa hàng bán được trong một tháng. Điều kiện của \[x\] và \(y\) để doanh thu của cửa hàng trong một tháng có lãi thoả mãn bất phương trình \(ax + by \le 1700\) với \(a,\,b \in \mathbb{N}\). Tính giá trị biểu thức \(T = 2a + b\).