Đề cương ôn tập giữa kì 1 Toán 12 Kết nối tri thức cấu trúc mới có đáp án - Bài 6. Vectơ trong không gian
38 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Cho hình hộp \[ABCD.{A_1}{B_1}{C_1}{D_1}\]. Chọn đẳng thức sai?
\(\overrightarrow {BC} - \overrightarrow {{B_1}{C_1}} = \overrightarrow {{B_1}{A_1}} - \overrightarrow {BA} \).
\(\overrightarrow {AD} + \overrightarrow {{D_1}{C_1}} + \overrightarrow {{D_1}{A_1}} = \overrightarrow {DC} \).
\(\overrightarrow {BC} + \overrightarrow {BA} + \overrightarrow {B{B_1}} = \overrightarrow {B{D_1}} \).
\(\overrightarrow {BA} + \overrightarrow {D{D_1}} + \overrightarrow {B{D_1}} = \overrightarrow {BC} \).
Cho hình hộp \(ABCD.A'B'C'D'\).
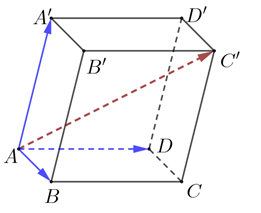
Vectơ \(\overrightarrow {AC'} \) là kết quả của phép tính tổng nào sau đây?
\(\overrightarrow {AA'} + \overrightarrow {AD} + \overrightarrow {CD} \).
\(\overrightarrow {AA'} + \overrightarrow {B'C'} \).
\(\overrightarrow {AA'} + \overrightarrow {AD} + \overrightarrow {AB} \).
\(\overrightarrow {AA'} + \overrightarrow {A'B} + \overrightarrow {B'C'} \).
Cho hình lập phương \(ABCD.A'B'C'D'\). Mệnh đề nào sau đây sai?
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \).
\(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\).
\(\overrightarrow {AB} = \overrightarrow {CD} \).
Cho tứ diện\(ABCD\), gọi \(I\), \(J\) lần lượt là trung điểm của \(AB\) và \(CD\). Đẳng thức nào sai?
\[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)\].
\[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right)\].
\[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {DC} + \overrightarrow {AD} + \overrightarrow {BD} } \right)\].
\[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {CD} } \right)\].
Cho tứ diện \(ABCD\). Mệnh đề nào dưới đây là mệnh đề đúng?
\(\overrightarrow {BC} + \overrightarrow {AB} = \overrightarrow {DA} - \overrightarrow {DC} \).
\(\overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {BD} - \overrightarrow {BC} \).
\(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {DB} - \overrightarrow {DC} \).
\(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {CD} + \overrightarrow {BC} \).
Cho tứ diện \[ABCD\]. Gọi \[I,J\] lần lượt là trung điểm của \[AB\] và \[CD\], \[G\] là trung điểm của \[IJ\]. Cho các đẳng thức sau, đẳng thức nào đúng?
\[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \].
\[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = 2\overrightarrow {{\rm{IJ}}} \].
\[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow {JI} \].
\[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = - 2\overrightarrow {JI} \].
Cho tứ diện đều ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB, AC. Góc giữa hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {BD} \).
\(150^\circ \).
\(120^\circ \).
\[30^\circ \].
\[60^\circ \].
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và mặt bên SAB là tam giác đều. Tính góc giữa hai vectơ \(\overrightarrow {DC} \) và \(\overrightarrow {BS} \).
\(150^\circ \).
\(120^\circ \).
\[90^\circ \].
\[60^\circ \].
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác \(\overrightarrow 0 \). Xác định góc \(\alpha \) giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khi \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\)
\(\alpha = {180^{\rm{o}}}\) .
\(\alpha = {0^{\rm{o}}}\) .
\(\alpha = {90^{\rm{o}}}\) .
\(\alpha = {45^{\rm{o}}}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Mặt bên ASB là tam giác vuông cân tại \(S\) và có cạnh \(AB = a\). Tính \(\overrightarrow {DC} .\overrightarrow {AS} \).
\(\frac{a}{{\sqrt 2 }}\) .
\({a^2}\) .
\(\frac{{{a^2}}}{2}\) .
\(\frac{{{a^2}}}{{\sqrt 2 }}\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Một chiếc đèn chùm treo có khối lượng \(m = 5\;kg\) được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích \(SA,SB,SC,SD\) (tham khảo hình vẽ) sao cho \(S.ABCD\) là hình chóp tứ giác đều có \(\widehat {ASC} = 60^\circ \). Biết \(\vec P = m.\vec g\) trong đó \(\vec g\) là vectơ gia tốc rơi tự do có độ lớn \[10\;\,{\rm{m/}}{{\rm{s}}^2}\], \(\vec P\) là trọng lực tác động vật có đơn vị là \(N\), \(m\) là khối lượng của vật có đơn vị \(kg\). Khi đó:

a) \(\overrightarrow {SA} ,\overrightarrow {SB} ,\overrightarrow {SC} ,\overrightarrow {SD} \) là 4 vectơ đồng phẳng.
b) \(\left| {\overrightarrow {SA} } \right| = \left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right| = \left| {\overrightarrow {SD} } \right|\).
c) Độ lớn của trọng lực \(\vec P\) tác động lên chiếc đèn chùm bằng \(50\;N\).
d) Độ lớn của lực căng cho mỗi sợi xích bằng \(\frac{{25\sqrt 3 }}{2}\;N\).
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông, \(SA\)vuông góc với mặt phẳng \((ABCD)\).Gọi \[I,J\] lần lượt là trung điểm của \[SA,SC\]. \[G\]là trọng tâm tam giác \[SBD\].

a) \(\overrightarrow {AC} - \overrightarrow {AB} = \overrightarrow {AD} \).
b) \(\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AG} \).
c) \[\overrightarrow {{\rm{IJ}}} .\overrightarrow {BD} = \overrightarrow 0 \].
d) \({\overrightarrow {AG} ^2} = {\overrightarrow {AS} ^2} + {\overrightarrow {AB} ^2} + {\overrightarrow {AD} ^2}\).
Cho hình hộp \(ABCD.A'B'C'D'\). Khi đó:
a) Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {C'D'} \) bằng nhau.
b) Hai vectơ \(\overrightarrow {A'D} \) và \(\overrightarrow {CB'} \) đối nhau.
c) Hai vectơ \(\overrightarrow {A'B'} \) và \(\overrightarrow {AC} \) cùng phương với nhau.
d) Có 3 vectơ khác vectơ \(\overrightarrow 0 \) bằng vectơ \(\overrightarrow {BC} \).
Cho hình chóp tứ giác đều S.ABCD có O là tâm của đáy ABCD, cạnh đáy bằng a, cạnh bên bằng 2a.
a) Góc giữa hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {CB} \) là 0°.
b) Góc giữa hai vectơ \(\overrightarrow {BD} \) và \(\overrightarrow {BO} \) là 180°.
c) Cosin của góc giữa hai vectơ \(\overrightarrow {BA} \) và \(\overrightarrow {CS} \) bằng \(\frac{1}{4}\).
d) Góc giữa hai vectơ \(\overrightarrow {AO} \) và \(\overrightarrow {SD} \) bằng 60°.
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình chữ nhật. Biết rằng cạnh \[AB = a\], \[AD = 2a\], cạnh bên \[SA = 2a\] và vuông góc với mặt đáy. Gọi \[M\], \[N\] lần lượt là trung điểm của các cạnh \[SB\], \[SD\].
a) Hai vectơ \[\overrightarrow {AB\,} \], \[\overrightarrow {CD\,} \] là hai vectơ cùng phương, cùng hướng.
b) Góc giữa hai vectơ \[\overrightarrow {SC\,} \] và \[\overrightarrow {AC\,} \] bằng \[60^\circ \].
c) Tích vô hướng \[\overrightarrow {AM\,} \cdot \,\overrightarrow {AB\,} = \frac{{{a^2}}}{2}\].
d) Độ dài của vectơ \[\overrightarrow {AM\,} - \overrightarrow {AN\,} \] là \[\frac{{a\sqrt 3 }}{2}\].
Phần III. Trắc nghiệm trả lời ngắn
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, \(AB = 2a\), \(BC = a\). Hình chiếu vuông góc \(H\) của đỉnh \(S\) trên mặt phẳng đáy là trung điểm của cạnh \(AB\), góc giữa đường thẳng \(SC\) và mặt phẳng đáy bằng \(60^\circ \). Tính cosin góc giữa hai vectơ \(\overrightarrow {SB} \) và \(\overrightarrow {AC} \)(làm tròn đến hàng phần chục).
Một em nhỏ cân nặng 20 kg trượt trên cầu trượt dài 3 m. Biết rằng cầu trượt có góc nghiêng so với phương nằm ngang là 30°. Cho biết công A(J) sinh bởi một lực \(\overrightarrow F \) có dịch chuyển \(\overrightarrow d \) được tính bởi công thức \(A = \overrightarrow F .\overrightarrow d \). Hãy tính công sinh bởi trọng lực \(\overrightarrow P \) khi em nhỏ trượt hết chiều dài cầu trượt gia tốc rơi tự do \(g = 9,8\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}\).

. Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} ,\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một ô tô tại điểm M và ô tô đứng yên. Cho biết cường độ hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) đều bằng 25N và \(\widehat {AMB} = 60^\circ \). Tính cường độ lực \(\overrightarrow {{F_3}} \)(kết quả làm tròn đến hàng phần mười).

B. TỰ LUẬN
Tìm các khoảng đơn điệu và các điểm cực trị của hàm số sau:
a) \(y = - {x^3} + 3{x^2} - 4\); b) \(y = {x^4} + 4{x^3} - 1\).
Tìm các khoảng đơn điệu và cực trị của các hàm số sau
a) \(y = \frac{{2x + 1}}{{x + 1}}\); b) \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\).
Tìm các khoảng đơn điệu và cực trị của các hàm số sau
a) \(y = {x^2} + 4\ln \left( {3 - x} \right)\); b) \(y = \sqrt {{x^2} - 2x} \).
Tìm giá trị lớn nhất và nhỏ nhất (nếu có) của hàm số sau trên đoạn đã chỉ ra.
a) \(f\left( x \right) = - {x^3} + 3{x^2} + 10\) trên đoạn \(\left[ { - 3;1} \right]\).
b) \(f\left( x \right) = - 2{x^4} + 4{x^2} + 3\) trên đoạn \(\left[ {0;2} \right]\).
Tìm giá trị lớn nhất và nhỏ nhất (nếu có) của hàm số sau trên đoạn đã chỉ ra.
a) \(f\left( x \right) = \frac{{2x + 3}}{{x + 1}}\) trên đoạn \(\left[ {0;4} \right]\);
b) \(f\left( x \right) = \frac{{2{x^2} + 4x + 5}}{{{x^2} + 1}}\) trên \(\mathbb{R}\).
Tìm giá trị lớn nhất và nhỏ nhất (nếu có) của hàm số sau trên đoạn đã chỉ ra.
a) \(y = {e^{{x^3} - 3x + 3}}\) trên đoạn \(\left[ {0;2} \right]\); b) \(y = \frac{{{{\ln }^2}x}}{x}\) trên đoạn \(\left[ {1;{e^5}} \right]\).
Cho hàm số \(f\left( x \right)\) có đồ thị của hàm số \(y = f'\left( x \right)\) như hình vẽ.
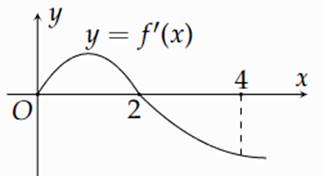
Biết \(f\left( 0 \right) + f\left( 1 \right) - 2f\left( 2 \right) = f\left( 4 \right) - f\left( 3 \right)\). Tìm giá trị lớn nhất M, giá trị nhỏ nhất m của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {0;4} \right]\).
Xác định tiệm cận đứng và tiệm cận ngang của đồ thị các hàm số sau
a) \(y = \frac{{2x - 1}}{{x + 1}}\);
b) \(y = \frac{{{x^2} - 5x + 4}}{{{x^2} - 1}}\).
Xác định tiệm cận đứng và tiệm cận xiên của đồ thị các hàm số sau
a) \(y = \frac{{{x^2} + 2}}{{2x - 4}}\); b) \(y = \frac{{2{x^2} + 9x + 11}}{{2x + 5}}\).
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau:
a) \(y = {x^3} - 3{x^2} + 1\);
b) \(y = {x^3} + 3{x^2} + 3x + 2\).
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên như hình bên.
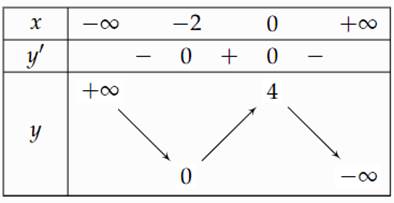
Xác định hàm số trên.
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau
a) \(y = \frac{{x - 1}}{{x + 1}}\);
b) \(y = \frac{{2x + 1}}{{x - 1}}\).
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau:
a) \(y = \frac{{{x^2} + 2x - 2}}{{x - 1}}\);b) \(y = - x + 2 - \frac{1}{{x + 1}}\).
Khi bỏ qua sức cản của không khí, độ cao (mét) của một vật được phóng thẳng đứng lên trên từ điểm cách mặt đất 2 m với vận tốc ban đầu 24,5 m/s là \(h\left( t \right) = 2 + 24,5t - 4,9{t^2}\) (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016).
a) Tìm vận tốc của vật sau 2 giây.
b) Khi nào vật đạt độ cao lớn nhất và độ cao lớn nhất đó là bao nhiêu?
c) Khi nào thì vật chạm đất và vận tốc của vật lúc chạm đất là bao nhiêu?
Xét phản ứng hoá học tạo ra chất \(C\) từ hai chất \(A\) và \(B\): . Giả sử nồng độ của hai chất \(A\) và \(B\) bằng nhau \(\left[ A \right] = \left[ B \right] = a\) (mol/l) . Khi đó nồng độ của chất \(C\) theo thời gian \(t\)\(\left( {t > 0} \right)\) được cho bởi công thức: \(\left[ C \right] = \frac{{{a^2}Kt}}{{aKt + 1}}\)(mol/l) trong đó \(K\) là hằng số dương.
a) Tìm tốc độ phản ứng tại thời điểm \(t > 0\).
b) Chứng minh nếu \(x = \left[ C \right]\) thì \(x'\left( t \right) = K{\left( {a - x} \right)^2}\)
c) Nêu hiện tượng xảy ra với nồng độ các chất khi \(t \to + \infty \)
d) Nêu hiện tượng xảy ra với tốc độ phản ứng khi \(t \to + \infty \)
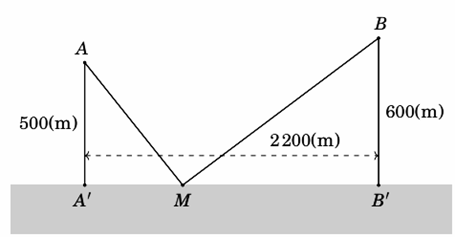
Có hai xã \(A,\,B\) cùng ở một bên bờ sông. Khoảng cách từ hai xã đó đến bờ sông lần lượt là \(AA' = 550\)m, \(BB' = 600\)m. Người ta đo được \(A'B' = 2200\)m như hình vẽ dưới đây. Các kỹ sư muốn xây dựng một trạm cung cấp nước sạch nằm cạnh bên bờ sông cho người dân của hai xã sử dụng. Để tiết kiệm chi phí, các kỹ sư phải chọn một vị trí \(M\) của trạm cung cấp nước sạch đó trên đoạn \(A'B'\) sao cho tổng khoảng cách từ hai xã đến vị trí \(M\) là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó.
Trong một bài thực hành huấn luyện quân sự có một tình huống chiến sĩ phải bơi qua sông để tấn công mục tiêu ở ngay phía bờ bên kia sông. Biết rằng lòng sông rộng 100m và vận tốc bơi của chiến sĩ bằng một phần ba vận tốc chạy trên bộ. Hãy cho biết chiến sỹ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất? Biết dòng sông là thẳng, mục tiêu cách chiến sỹ 1km theo đường chim bay và chiến sỹ cách bờ bên kia 100m.
Cho tứ diện ABCD. Chứng minh \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AD} + \overrightarrow {BC} \).
Cho tứ diện ABCD có AC và BD cùng vuông góc với AB. Gọi I, J lần lượt là trung điểm của hai cạnh AB, CD. Chứng minh \(IJ \bot AB\).
Cho hình lập phương \[ABCD.A'B'C'D'\] có cạnh bằng a. Gọi M, N lần lượt là trung điểm của \(A'D'\) và \(C'D'\). Tính tích vô hướng \(\overrightarrow {MN} .\overrightarrow {C'B} \).