Đề cương ôn tập cuối kì 1 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Bài 8. Biểu thức tọa độ của các phép toán vectơ
12 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Trong không gian Oxyz, cho điểm \[A\left( {2; - 3;5} \right)\]. Tìm tọa độ \[A'\] là điểm đối xứng với \[A\] qua trục \[Oy\].
\(A'\left( {2;3;5} \right)\).
\(A'\left( {2; - 3; - 5} \right)\).
\(A'\left( { - 2; - 3;5} \right)\).
\(A'\left( { - 2; - 3; - 5} \right)\).
Trong không gian với hệ trục tọa độ Oxyz, cho \(\vec a = \left( {2; - 3;3} \right)\), \(\vec b = \left( {0;2; - 1} \right)\), \(\vec c = \left( {3; - 1;5} \right)\). Tìm tọa độ của vectơ\(\vec u = 2\vec a + 3\vec b - 2\vec c\).
\(\left( {10; - 2;13} \right)\).
\(\left( { - 2;2; - 7} \right)\).
\(\left( { - 2; - 2;7} \right)\).
\(\left( { - 2;2;7} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A\(\left( {1; - 3;1} \right)\), B\(\left( {3;0; - 2} \right)\). Tính độ dài \(AB\).
26.
22.
\(\sqrt {26} \).
\(\sqrt {22} .\)
Trong không gian với hệ tọa độ Oxyz cho hai điểm \(A\left( {3; - 2;3} \right)\)và \(B\left( { - 1;2;5} \right)\).Tìm tọa độ trung điểm\(I\)của đoạn thẳng \(AB\) là :
\(I\left( { - 2;2;1} \right)\).
\(I\left( {1;0;4} \right)\).
\(I\left( {2;0;8} \right)\).
\(I\left( {2; - 2; - 1} \right)\).
Trong không gian Oxyz, cho \(\overrightarrow u = \left( {1;2;3} \right)\), \(\overrightarrow v = \left( {0; - 1;1} \right)\). Tìm tọa độ của một vectơ khác \(\overrightarrow 0 \) vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
\(\left( {5;1; - 1} \right)\).
\(\left( {5; - 1; - 1} \right)\).
\(\left( { - 1; - 1; - 1} \right)\).
\(\left( { - 1; - 1;5} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho tam giác \(ABC\) có \(A\left( {1;0;0} \right)\), \(B\left( {0;0;1} \right)\), \(C\left( {2;1;1} \right)\). Diện tích của tam giác \(ABC\) bằng:
\(\frac{{\sqrt {11} }}{2}\).
\(\frac{{\sqrt 7 }}{2}\).
\(\frac{{\sqrt 6 }}{2}\).
\(\frac{{\sqrt 5 }}{2}\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow a = ( - 2;1; - 3),\overrightarrow b = ( - 1; - 3;2)\) và điểm \(A\left( {4;6; - 3} \right)\).
a)Tọa độ vectơ \(\overrightarrow a - 2\overrightarrow b = (0;1; - 1).\)
b)Tọa độ điểm \(B\left( {2;7; - 6} \right)\) thì \(\vec a = \overrightarrow {AB} .\)
c) Hai vectơ \(\vec a\) và \(\vec b\) cùng phương hướng.
d) Góc giữa vectơ \(\vec a\) và \(\vec b\)bằng \(120^\circ .\)
Hình minh hoạ sơ đồ một ngôi nhà trong hệ trục tọa độ Oxyz, trong đó nền nhà, bốn bức tường và hai mái nhà đều là hình chữ nhật.
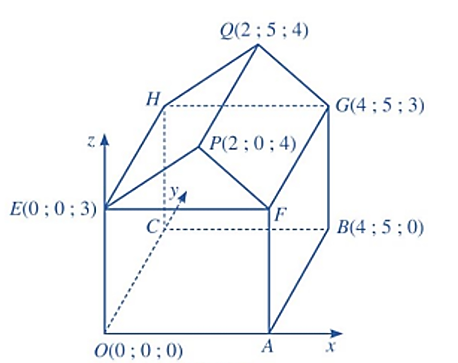
a) Tọa độ điểm \(A\) là \((4;0;0)\).
b) Tọa độ \(\overrightarrow {AH} = \left( {4;5;3} \right)\)
c)\(\overrightarrow {AH} .\overrightarrow {AF} = 3\)
d) Góc dốc của mái nhà, tức là số đo của góc nhị diện có cạnh là đường thẳng \(FG\), hai mặt lần lượt là \((FGQP)\) và \((FGHE)\) bằng \(26,6^\circ \) (làm tròn kết quả đến hàng phần mười của độ)
Trong không gian hệ tọa độ Oxyz cho hai điểm \(M\left( { - 4;3; - 1} \right)\) và \(N\left( {2; - 1; - 3} \right)\).
a) \(\overrightarrow {OM} = \left( { - 4;3; - 1} \right)\).
b) Cho \(\overrightarrow v = \overrightarrow i + 2\overrightarrow j - 3\overrightarrow k \) và \(\overrightarrow {AM} = \overrightarrow v \). Khi đó \(A\left( {5;1;2} \right)\).
c) Gọi G là trọng tâm của DOMN. Tọa độ hình chiếu của \(G\) trên \(\left( {Oxy} \right)\) là \(\left( {0;0; - \frac{4}{3}} \right)\).
d) I là trung điểm của đoạn MN. Tọa độ của vectơ \(\overrightarrow w = 3\overrightarrow i + 2\overrightarrow {ON} - \frac{1}{2}\overrightarrow {OI} \) là \(\left( {\frac{9}{2}; - \frac{5}{2}; - 7} \right)\).
Phần III. Trắc nghiệm trả lời ngắn
Trong không gian với hệ tọa độ Oxyz cho các vectơ \(\overrightarrow u = 2\overrightarrow i - 2\overrightarrow j + \overrightarrow k \), \(\overrightarrow v = \left( {m;\,2;\,m + 1} \right)\) với \(m\) là tham số thực. Có bao nhiêu giá trị của \(m\) để \(\left| {\overrightarrow u } \right| = \left| {\overrightarrow v } \right|\)?
Trong không gian với hệ tọa độ Oxyz cho hai điểm \(A\left( {4;\,\,2;\,\,1} \right)\), \(B\left( { - 2;\, - 1;\,4} \right)\). Tìm được tọa độ điểm \(M\left( {a;b;c} \right)\) thỏa mãn đẳng thức \(\overrightarrow {AM} = 2\overrightarrow {MB} \). Khi đó \(a + b + c = ?\)
Trong không gian Oxyz, cho hai điểm \(A\left( {1;0;0} \right)\) và \(B\left( { - \sqrt 3 ;1;0} \right)\). Số đo góc \(\widehat {AOB}\) của tam giác \(OAB\) bằng bao nhiêu độ?