Đề cương ôn tập cuối kì 1 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Bài 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn
12 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Một chất điểm chuyển động có phương trình \(S = {t^3} - 3{t^2} - 9t + 2\), trong đó t được tính bằng giây và S được tính bằng mét. Gia tốc tại thời điểm vận tốc bị triệt tiêu là:
\[ - 9{\rm{m/}}{{\rm{s}}^{\rm{2}}}\].
\[9{\rm{m/}}{{\rm{s}}^{\rm{2}}}\].
\[ - 12{\rm{m/}}{{\rm{s}}^{\rm{2}}}\].
\[12{\rm{m/}}{{\rm{s}}^{\rm{2}}}\].
Một vật chuyển động theo quy luật \[s = \frac{1}{3}{t^3} - {t^2} + 9t\], vớit (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường đi được trong thời gian đó. Hỏi trong khoảng thời gian 10 giây kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
\[89\left( {{\rm{m/s}}} \right).\]
\[71\left( {{\rm{m/s}}} \right).\]
\[109\left( {{\rm{m/s}}} \right).\]
\[\frac{{25}}{3}\left( {{\rm{m/s}}} \right)\].
Ông A dự định sử dụng hết \(8{\rm{ }}{{\rm{m}}^{\rm{2}}}\)kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng. Bể cá có dung tích lớn nhất bằng bao nhiêu ?
\[2,05{\rm{ }}{{\rm{m}}^{\rm{3}}}\].
\[1,02{\rm{ }}{{\rm{m}}^{\rm{3}}}\].
\[1,45{\rm{ }}{{\rm{m}}^{\rm{3}}}\].
\[0,73{\rm{ }}{{\rm{m}}^3}\].
Đồ thị bên dưới là tốc độ của một chiếc xe đua trên đoạn đường đua bằng phẳng dài 3 km.
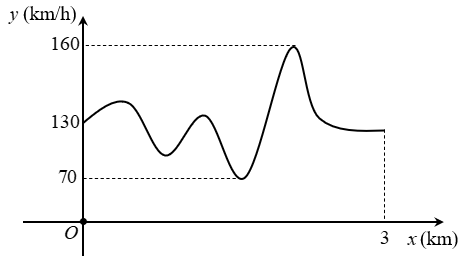
Tốc độ nhỏ nhất của xe đua trên đoạn đường này bằng
\(3\,\)(km/h).
\(160\,\)(km/h).
\(130\,\)(km/h).
\(70\,\)(km/h).
Giả sử số lượng của một quần thể nấm \(X\) tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hóa bằng hàm số \[P\left( t \right) = 120{{\rm{e}}^{0,15t}}\], trong đó thời gian \(t\) được tính bằng giờ. Tại thời điểm ban đầu \(t = 0\), tốc độ tăng trưởng của quần thể nấm \(X\) là
18 tế bào/giờ.
120 tế bào/giờ.
15 tế bào/giờ.
102 tế bào/giờ.
Giả sử số lượng \(x\) sản phẩm bán ra của một loại hàng hóa phụ thuộc vào giá bán \(p\) (nghìn đồng, \(p < 250\)) của nó theo công thức \(x = \frac{{250 - p}}{{0,01p}}\). Khẳng định nào sau đây đúng?
Số lượng sản phẩm bán ra luôn tăng khi giá bán tăng.
Số lượng sản phẩm bán ra không đổi khi giá bán giảm.
Số lượng sản phẩm bán ra luôn giảm khi giá bán giảm.
Số lượng sản phẩm bán ra luôn giảm khi giá bán tăng.
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Nhà máy\(A\) chuyên sản xuất một loại sản phẩm cho nhà máy\(B\). Hai nhà máy thỏa thuận rằng, hằng tháng \(A\) cung cấp cho \(B\) số lượng sản phẩm theo đơn đặt hàng của \(B\) (tối đa \(100\) tấn sản phẩm). Nếu số lượng đặt hàng là \(x\) tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm được biểu diễn bởi công thức: \(P\left( x \right) = 45 - 0,001{x^2}\) (triệu đồng). Cho phí để \(A\) sản xuất \(x\) tấn sản phẩm trong một tháng là \(C\left( x \right) = 100 + 30x\) triệu đồng (gồm \(100\)triệu đồng chi phí cố định và \(30\) triệu đồng cho mỗi tấn sản phẩm).
a) Chi phí để \(A\) sản xuất \(10\) tấn sản phẩm trong một tháng là \(400\)triệu đồng.
b) Số tiền \(A\) thu được khi bán \(10\) tấn sản phẩm cho \(B\) là \(600\)triệu đồng.
c) Lợi nhuận mà \(A\) thu được khi bán \(x\) tấn sản phẩm \(\left( {0 \le x \le 100} \right)\) cho \(B\) được biểu diễn bởi công thức \(H\left( x \right) = - 0,001{x^3} + 15x - 100\).
d) Bên \(A\) bán cho \(B\) khoảng \(70,7\) tấn sản phẩm mỗi tháng thì thu được lợi nhuận lớn nhất.
Tại một cơ sở sản xuất nước tinh khiết, nhân viên phụ trách sản xuất cho biết, nếu mỗi ngày cơ sở này sản xuất \(x\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\) nước tinh khiết thì phải chi phí các khoản sau: 5 triệu đồng chi phí cố định; \(0,15\) triệu đồng cho mỗi mét khối sản phẩm; \(0,0005{x^2}\)chi phí bảo dưỡng máy móc. Biết công suất tối đa mỗi ngày của cơ sở này là \(200\;{{\rm{m}}^{\rm{3}}}\). Gọi \(C\left( x \right)\) là chi phí sản suất \(x\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\) sản phẩm mỗi ngày và \(\overline c \left( x \right)\)là chi phí trung bình mỗi mét khối sản phẩm.
a) \(C\left( x \right) = 0,0005{x^2} + 0,15x + 5\).
b) Chi phí sản suất \(100{{\rm{m}}^{\rm{3}}}\) nước tinh khiết là 20 triệu đồng.
c)\(\overline c \left( x \right) = 0,0005x + 0,15 + \frac{5}{x}\).
d) Chi phí trung bình giảm xuống khi sản lượng nước tính khiết trong ngày không vượt quá \({\rm{100}}\;{{\rm{m}}^3}.\)
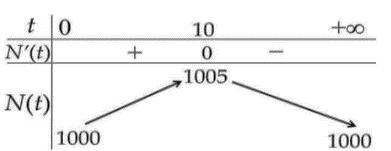
Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức \(N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}}\) (con), trong đó \(t\) là thời gian tính bằng giây.
a) Đến giây thứ 10 thì số lượng vi khuẩn đạt nhiều nhất.
b) Thời gian tăng lên nhiều giờ thì số lượng vi khuẩn càng nhiều.
c) Sau khi cấy lại môi trường dinh dưỡng, số lượng vi khuẩn tăng thêm được 3 con so với lúc đầu tại hai thời điểm \({t_1}\) và \({t_2}\). Khi đó \({t_1}{t_2} = 100\).
d) Bảng biến thiên của hàm số \(N\left( t \right)\) như hình
Phần III. Trắc nghiệm trả lời ngắn
Một hộ làm nghề dệt vải lụa tơ tằm sản suất mỗi ngày được \(x\) mét vải lụa \(\left( {1 \le x \le 18} \right)\). Tổng chi phí sản xuất \(x\) mét vải lụa, tính bằng nghìn đồng, cho bởi hàm chi phí:\(C\left( x \right) = {x^3} - 3{x^2} - 20x + 500.\)
Giả sử hộ làm nghề dệt này bán hết sản phẩm mỗi ngày với giá 220 nghìn đồng/mét. Gọi \(L\left( x \right)\) là lợi nhuận thu được khi bán \(x\) mét vải lụa. Hỏi lợi nhuận tối đa của hộ làm nghề dệt vải lụa tơ tằm trong một ngày là bao nhiêu nghìn đồng?
Giả sử doanh số bán hàng (đơn vị triệu đồng) của một sản phẩm mới trong vòng một số năm nhất định tuân theo quy luật logistic được mô hình hóa bằng hàm số \(f\left( t \right) = 500\left( {{t^2} + m{e^{ - t}}} \right)\), với \(t \ge 0\) là thời gian tính bằng năm kể từ khi phát hành sản phẩm mới, \(m \le 0\) là tham số. Khi đó đạo hàm \(f'\left( t \right)\) sẽ biểu thị tốc độ bán hàng. Biết rằng tốc độ bán hàng luôn tăng trong khoảng thời gian 10 năm đầu phát hành sản phẩm, khi đó giá trị nhỏ nhất của \(m\) bằng bao nhiêu?
Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất 8000 quả bóng tennis. Biết công ty này có 38 máy và mỗi máy có thể sản xuất 30 quả bóng trong một giờ. Chi phí thiết lập các máy này là 200 nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giảm sát. Số tiền phải trả cho người giám sát là 192 nghìn đồng một giờ. Số máy công ty nên sử dụng để sản xuất đơn hàng trên là bao nhiêu để chi phí hoạt động là thấp nhất?