Đề cương ôn tập cuối kì 1 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Bài 6. Vectơ trong không gian
12 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Trong không gian cho 3 điểm \[M,{\rm{ }}N,{\rm{ }}P\] phân biệt. Tính \(\overrightarrow {PM} + \overrightarrow {MN} \).
\[\overrightarrow {NM} \].
\[\overrightarrow {MN} \].
\[\overrightarrow {NP} \].
\[\overrightarrow {PN} \].
Cho hình lập phương \[ABCD.A'B'C'D'\]. Vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương \[ABCD.A'B'C'D'\] và bằng vectơ \(\overrightarrow {AD} \) là
![Do \[ABCD.A'B'C'D'\] là hình l (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/11-1761391014.png)
\[\overrightarrow {B'C'} \].
\[\overrightarrow {DA} \].
\[\overrightarrow {CB} \].
\[\overrightarrow {AB} \].
Cho hình hộp \[ABCD.EFGH\]. Kết quả quả phép toán \[\overrightarrow {AB} - \overrightarrow {EH} \]là
![Cho hình hộp \[ABCD.EFGH\]. Kết quả quả phép toán \[\overrightarrow {AB} - \overrightarrow {EH} \] là A. \[\overrightarrow {BD} \]. B. \[\overrightarrow {AE} \]. C. \[\overrightarrow {DB} \]. D. \[\overrightarrow {BH} \]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/12-1761391058.png)
\[\overrightarrow {BD} \].
\[\overrightarrow {AE} \].
\[\overrightarrow {DB} \].
\[\overrightarrow {BH} \].
Trong không gian, cho hình lập phương \(ABCD.A'B'C'D'\). Góc giữa hai vectơ \(\overrightarrow {BD} \,,\,\overrightarrow {B'C} \)bằng
\(30^\circ \).
\(45^\circ \).
\(60^\circ \).
\(90^\circ \).
Cho \(\left| {\overrightarrow a } \right| = 2;\;\left| {\overrightarrow b } \right| = 6\), góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) bằng \(120^\circ \). Khẳng định nào dưới đây đúng?
\(\overrightarrow a .\overrightarrow b = 12\).
\[\overrightarrow a .\overrightarrow b = 40\].
\[\overrightarrow a .\overrightarrow b = - 6\].
\[\overrightarrow a .\overrightarrow b = 6\sqrt 3 \].
Nếu một vật có khối lượng \(m\;\left( {{\rm{kg}}} \right)\) thì lực hấp dẫn \(\vec P\) của Trái Đất tác dụng lên vật được xác định theo công thức \(\vec P = m\vec g\), trong đó \(\vec g\) là gia tốc rơi tự do có độ lớn \(g = 9,8\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}\). Tính độ lớn của lực hấp dẫn của Trái Đất tác dụng lên một quả táo có khối lượng 102 gam (Hình).
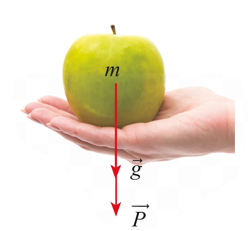
\(0,9996{\rm{N}}\).
\(0,5996{\rm{N}}\).
\(0,9196{\rm{N}}\).
\(0,8996{\rm{N}}\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông, \(SA\)vuông góc với mặt phẳng \((ABCD)\). Gọi \[I,J\] lần lượt là trung điểm của \[SA,SC\]. \[G\]là trọng tâm tam giác \[SBD\].
![Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là h (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/15-1761392134.png)
a) \(\overrightarrow {AC} - \overrightarrow {AB} = \overrightarrow {AD} \).
b) \(\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AG} \).
c) \[\overrightarrow {{\rm{IJ}}} .\overrightarrow {BD} = \overrightarrow 0 \].
d) \({\overrightarrow {AG} ^2} = {\overrightarrow {AS} ^2} + {\overrightarrow {AB} ^2} + {\overrightarrow {AD} ^2}\).
Cho hình lập phương \[ABCD.A'B'C'D'\], có cạnh \(a\).
a)\[\overrightarrow {AD'} .\overrightarrow {CC'} = {a^2}\].
b) \[\overrightarrow {AD'} .\overrightarrow {AB'} = {a^2}\].
c)\[\overrightarrow {AB'} .\overrightarrow {CD'} = 0\].
d) \[\left| {\overrightarrow {AC'} } \right| = a\sqrt 3 \].
Một vật nặng O được kéo từ ba hướng như hình vẽ và chịu tác dụng của 3 lực \[\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \] có độ lớn lần lượt là \(24N,12N,6N\). Biết góc tạo bởi 2 lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) là 120° và lực thứ ba vuông góc với hai lực đầu tiên.
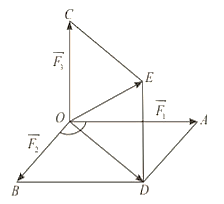
a)\(\overrightarrow {BO} + \overrightarrow {BA} = \overrightarrow {BD} \).
b) \(\overrightarrow {OE} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} \).
c) Độ dài của vectơ \(\overrightarrow {OD} \) là \(\left| {\overrightarrow {OD} } \right| = 12\sqrt 7 \).
d) Độ lớn hợp lực tác dụng vào vật \(O\) là \(6\sqrt {13} \) N.
Phần III. Trắc nghiệm trả lời ngắn
Cho tứ diện \(ABCD\). Gọi \(E\) là trung điểm \(AD\), \(F\) là trung điểm \(BC\). Khi đó \[\overrightarrow {AB} + \overrightarrow {DC} = k\overrightarrow {EF} \]. Tìm \(k\).
Chohình lập phương \(ABCD.A'B'C'D'\). Góc giữa hai véctơ \(\overrightarrow {A'B} \) và \(\overrightarrow {AC'} \) bằng bao nhiêu độ?
Cho tứ diện đều \(ABCD\) có độ dài cạnh bằng 1, gọi \(M\) là trung điểm cạnh \(CD\). Tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AM} \) bằng bao nhiêu?