Đề cương ôn tập giữa kì 1 Toán 12 Kết nối tri thức cấu trúc mới có đáp án - Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
19 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Đồ thị được cho trong hình vẽ dưới đây là của hàm số nào?

\[y = {\rm{ }}{x^4} - 2{x^2}\].
\[y = {x^{\rm{3}}} - 3x - 1\].
\[y = - {x^{\rm{3}}} + 3x\].
\[y = {x^3} - 3x\].
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào?
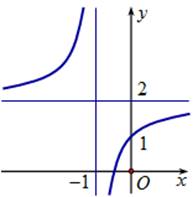
\(y = \frac{{2x - 1}}{{x + 1}}\).
\(y = \frac{{2x + 1}}{{x + 1}}\).
\(y = \frac{{2x - 1}}{{x - 1}}\).
\(y = \frac{{2x + 1}}{{x - 1}}\).
Bảng biến thiên ở hình dưới là của một trong bốn hàm số được liệt kê dưới đây. Hãy tìm hàm số đó.

\(y = \frac{{2x - 3}}{{x + 1}}\).
\(y = \frac{{2x + 3}}{{x + 1}}\).
\(y = \frac{{ - 2x - 3}}{{x + 1}}\).
\(y = \frac{{ - x + 1}}{{x - 2}}\).
Đồ thị hàm số \(y = {x^3} - 3x + 2\) là hình nào trong 4 hình dưới đây?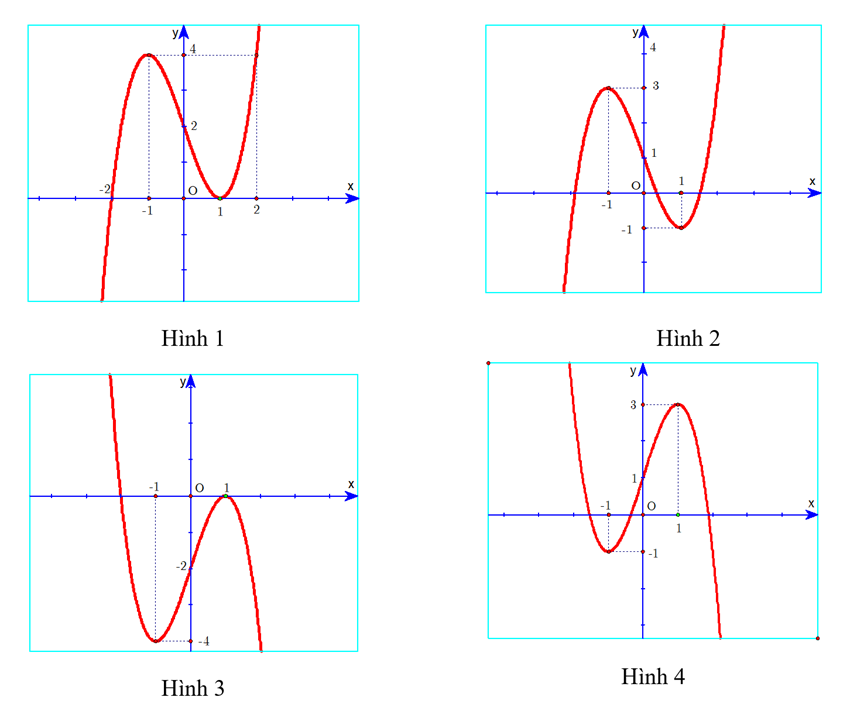
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Cho hàm số \[y = a{x^3} + b{x^2} + cx + d\] có đồ thị như hình vẽ bên dưới.
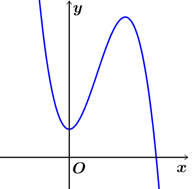
Mệnh đề nào dưới đây đúng?
\[a < 0,b > 0,c > 0,d > 0\].
\[a < 0,b < 0,c = 0,d > 0\].
\[a > 0,b < 0,c > 0,d > 0\].
\[a < 0,b > 0,c = 0,d > 0\].
Cho hàm số \(y = \frac{{x + b}}{{cx + d}}\) có đồ thị như hình vẽ bên
Xác định dấu của các hệ số \(b\), \(c\), \(d\).
\(b < 0,\,c > 0,\,d > 0\).
\(b < 0,\,c > 0,\,d < 0\).
\(b > 0,\,c < 0,\,d > 0\).
\(b > 0,\,c < 0,\,d < 0\).
Đường cong trong hình là đồ thị của hàm số nào dưới đây?

\(y = \frac{{ - {x^2} + 1}}{x}\).
\(y = \frac{{ - 2x + 1}}{{2x + 2}}\).
\(y = \frac{{{x^2} - x + 1}}{{x - 1}}\).
\(y = {x^3} - 3{x^2}\).
Bảng biến thiên sau là của một trong bốn hàm số sau.
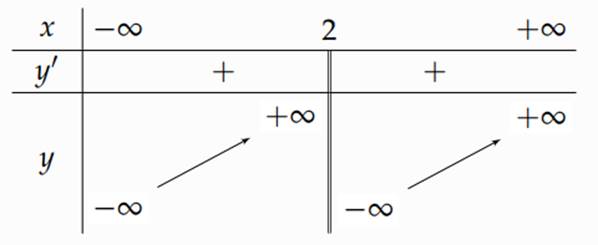
Hỏi đó là hàm số nào?
\(y = \frac{{{x^2} - 3}}{{x - 2}}\).
\(y = \frac{{{x^2} - 4x + 2}}{{x - 2}}\).
\(y = \frac{{{x^2} - x}}{{x - 2}}\).
\(y = \frac{{{x^2} - 4x + 5}}{{x - 2}}\).
Đườngcongtronghìnhbênlàđồthịcủahàmsố nào?

\(y = \frac{{{x^2} - x - 1}}{{x + 2}}\).
\(y = \frac{{{x^2} - x - 1}}{{x - 2}}\).
\(y = \frac{{{x^2} - 2x - 1}}{{x - 2}}\).
\(y = \frac{{{x^2} - x + 1}}{{x - 2}}\).
Đồ thị của hàm số nào dưới đây có dnagj như đường cong trong hình sau.

\(y = \frac{{2x + 1}}{{x + 1}}\).
\(y = {x^3} - 3x - 1\).
\(y = \frac{{2x - 1}}{{x + 1}}\).
\(y = \frac{{2{x^2} + 3x + 2}}{{x + 1}}\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{ - {x^2} + x + 1}}{{x + 1}}\) có đồ thị (C).
a) Hàm số đồng biến trên khoảng \(( - 2, - 1)\) và \(( - 1,0)\).
b) Hàm số có hai điểm cực trị.
c) Đồ thị \((C)\) không cắt trục \(Ox\).
d) Đồ thị \((C)\) có tiệm cận xiên đi qua điểm \(A(1;2)\)
Cho hàm số \(y = \frac{{m{x^2} + (3{m^2} - 2)x - 2}}{{x + 3m}}\) (1), với \(m\) là số thực.
a) Khi \(m = 1\) đồ thị hàm số có 2 điểm cực trị.
b) Khi \(m = 1\) đồ thị hàm số có đường tiệm cận xiên là \(y = x - 2\).
c) Khi \(m = 1\) giao điểm của đường tiệm cận xiên và tiệm cận đứng của đồ thị hàm số là \(I\left( {3; - 5} \right)\).
d) Có 2 giá trị \(m\) để góc giữa hai tiệm cận của đồ thị hàm số (1) bằng \(45^\circ \).
Cho hàm số \(y = \frac{{{x^2} + x + 1}}{{x + 1}}\).
a) Hàm số đã cho đồng biến trên các khoảng \(( - \infty ; - 2)\) và \((0; + \infty )\).
b) Hàm số đã cho không có cực trị.
c) Đồ thị hàm số có đường tiệm cận xiên là \(y = x\).
d) Đồ thị hàm số có tâm đối xứng là \(I( - 1; - 1)\).
Cho hàm số \(f\left( x \right) = \frac{1}{2}{x^3} - \frac{3}{2}x + 2\)
a) Hàm số đã cho có đạo hàm \(f'\left( x \right) = \frac{3}{2}{x^2} - \frac{3}{2},\forall x \in \mathbb{R}\).
b) Hàm số đã cho nghịch biến trên khoảng \(\left( { - 1;1} \right)\) và đồng biến trên các khoảng\(\left( { - \infty ; - 1} \right)\)và \(\left( {1; + \infty } \right)\).
c) Đồ thị hàm số đã cho có 2 điểm cực trị là \(x = - 1\) và \(x = 1\).
d) Có \(3\) giá trị nguyên của tham số \(m\) để phương trỉnh \(f\left( x \right) = m\) có \(3\) nghiệm phân biệt.
Cho hàm số \(y = f(x) = \frac{{{x^2} + 3x + 3}}{{x + 2}}\) có đồ thị là đường cong \((C)\)
a) Hàm số nghịch biến trên khoảng \(\left( { - 3\,;\, - 2} \right)\) và \(\left( { - 2\,;\, - 1} \right)\).
b) Biết hàm số có 2 điểm cực trị khi đó tổng của giá trị cực đại và giá trị cực tiểu bằng \( - 4\).
c) Tiệm cận xiên của đồ thị hàm số là đường thẳng \(y = - x + 1\).
d) Tiếp tuyến với \((C)\) vuông góc với đường thẳng \(x - 3y - 6 = 0\) đi qua điểm \(B\left( { - \frac{3}{2},\frac{3}{2}} \right)\).
Phần III. Trắc nghiệm trả lời ngắn
Cho hàm số \(y = \frac{{ax + b}}{{x + c}}\) có đồ thị như hình bên dưới, với \(a\), \(b\), \(c \in \mathbb{Z}\). Tính giá trị của biểu thức \(T = a + 2b + 3c\).

Đồ thị trong hình bên dưới là của hàm số \(y = \frac{{ax + b}}{{x + c}}\) (với \(a,b,c \in \mathbb{R}\)).

Tính\(a + b + c\).
Đồ thị trong hình bên dưới là của hàm số \(y = ax + b + \frac{1}{{x + c}}\).
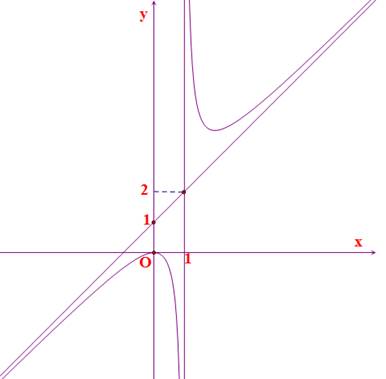
Tính \(a + b + c\).
Cho hàm số \(y = \frac{{a{x^2} + bx + c}}{{x + d}}(a,b,c,d \in \mathbb{R})\) có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số \(a,b,c,d\)?