Đề cương ôn tập giữa kì 1 Toán 12 Kết nối tri thức cấu trúc mới có đáp án - Bài 3. Đường tiệm cận của đồ thị hàm số
18 câu hỏi
Cho hàm số xác định trên , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau

Hỏi đồ thị hàm số trên có bao nhiêu đường tiệm cận?
0.
1.
2.
3
Hàm số có bảng biến thiên như hình vẽ dưới đây.

Cho các khẳng định sau:
(1) Đồ thị hàm số có tiệm cận đứng
(2) Hàm số đạt giá trị cực đại tại
(3) Hàm số đồng biến trên .
(4) Hàm số có tiệm cận ngang
Số khẳng định đúng là:
1.
4.
2.
0
Hàm số \(y = f\left( x \right)\) liên tục trên các khoảng xác định và có bảng biến thiên như hình vẽ dưới đây.

Tìm m để \[\mathop {\lim }\limits_{x\, \to \, + \infty } \,f\left( x \right)\, < 10.\]
\(m < 1\).
\(m < 10\).
\(m < 8\).
\(m > 8\)
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên sau:

Tìm tổng số các giá trị nguyên dương của tham số \(m \in \left( { - 10\,;\,10} \right)\) để đồ thị hàm số \(y = f\left( x \right)\) có tổng số đường tiệm cận đứng và đường tiệm cận ngang là \(4\).
\(42\).
\(45\).
\( - 3\).
\(0\).
Đường thẳng \[y = - 1\]là tiệm cận ngang của đồ thị hàm số nào sao đây?
\(y = \frac{{1 + x}}{{1 - x}}\).
\[y = \frac{{x - 2}}{{x + 2}}\].
\[y = \frac{{ - {x^2} + 2}}{{x + 1}}\].
\[y = \frac{{ - 1 - x}}{{1 - x}}\].
Cho hàm số \(y = \frac{{3x - 1}}{{x + 1}}\). Chọn phát biểu đúng?
Đồ thị hàm số có \(y = 3\) là tiệm cận đứng.
Giao điểm hai tiệm cận là \(\left( {3; - 1} \right)\).
Đồ thị có tiệm cận đứng có phương trình là \(x + 1 = 0\).
Hai tiệm cận tạo với hai trục tọa độ một hình vuông có diện tích là 3.
Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ dưới. Chọn khẳng định sai.

Đồ thị hàm số có tiệm cận đứng \(x = - 1.\)
Đồ thị hàm số có tiệm cận ngang \(y = 2.\)
Đồ thị hàm số có tâm đối xứng là \(I\left( {2; - 1} \right)\).
Đồ thị hàm số có hai đường tiệm cận.
Hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

\(y = \frac{{2 - x}}{{x - 1}}\).
\(y = \frac{{x - 1}}{{x + 1}}\).
\(y = \frac{{x - 2}}{{x - 1}}\).
\(y = \frac{{x + 1}}{{x - 1}}\).
Đường tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = x + 3 + \frac{1}{{2x + 1}}\) có phương trình là
\(y = 2x + 1\).
\(y = x - 3\).
\(y = x + 3\).
\(y = 2x - 1\)
Tìm tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} + 3x}}{{x - 2}}\)
\(y = 2x - 5\).
\(y = x - 2\).
\(y = x + 5\).
\(y = x - 5\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên dưới

a) \(f\left( { - 5} \right) < f\left( 4 \right)\).
b) Hàm số có giá trị nhỏ nhất bằng 2.
c) Đồ thị hàm số có tiệm cận đứng \(x = 0\).
d) Đồ thị hàm số không có tiệm cận ngang.
Cho hàm số \(y = \frac{{2x - 3}}{{ - x + 1}}\).
a) Bảng biến thiên của hàm số là

b) Tâm đối xứng của đồ thị hàm số là \(I\left( {1; - 2} \right)\).
c) Đường tiệm cận đứng của đồ thị hàm số là \(x = - 2\).
d) Đường tiệm cận ngang của hàm số là \(y = 1\).
Cho đồ thị hàm số \(y = f\left( x \right) = \frac{{2{x^2}}}{{{x^2} - 1}}\).
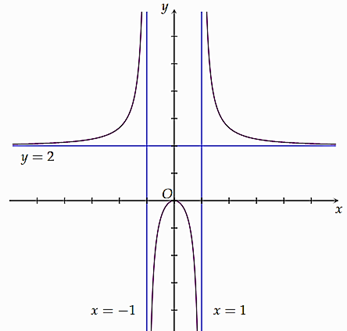
a) Đồ thị hàm số có 3 điểm cực trị.
b) \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2;\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = - \infty \).
c) Đồ thị hàm số có 3 đường tiệm cận đứng là \(x = - 1;x = 0;x = 1\).
d) Đồ thị hàm số có hai đường tiệm cận ngang \(y = 2\) và \(y = 0\).
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau
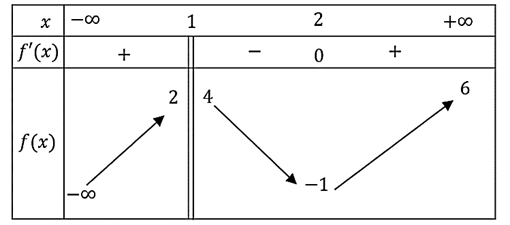
a) Đồ thị hàm số có đường tiệm cận đứng là \[x = 1\].
b) Đồ thị hàm số có đường tiệm cận ngang là \[y = 6\].
c) Tổng số đường tiệm cận của đồ thị hàm số đã cho là \[2\].
d) Tổng số tiệm cận ngang của đồ thị hàm số \[y = \frac{1}{{f(x) + 2}}\] là \[1\].
Cho hàm số có đồ thị \(\left( C \right)\).
a) Đồ thị (C) có tiệm cận ngang là đường thẳng \(x = - 1\).
b) Đường thẳng \(y = x + 1\)là tiệm cận xiên của đồ thị \(\left( C \right)\).
c) Hàm số nghịch biến trên khoảng \(\left( { - 4; - 1} \right)\) và \(\left( { - 1;2} \right)\).
d) Đường thẳng đi qua điểm cực đại và điểm cực tiểu của đồ thị hàm số là \(y = 2x + 3\).
Phần III. Trắc nghiệm trả lời ngắn
Cho hàm số \(y = \frac{{ax + 1}}{{bx - 2}}\). Khi đó \(a + b\) bằng bao nhiêu để đồ thị của hàm số trên nhận đường thẳng \(x = 1\) làm tiệm cận đứng và đường thẳng \(y = \frac{1}{2}\) làm tiệm cận ngang.
Có bao nhiêu giá trị của tham số thực m để đồ thị hàm số \(y = \frac{{{x^2} + m}}{{{x^2} - 3x + 2}}\) có đúng hai đường tiệm cận.
Số lượng sản phẩm bán được của một cửa hàng quần áo trong \(t\) (tháng) được cho bởi công thức: \(S\left( t \right) = 200\left( {\frac{2}{3} - \frac{8}{{2 + t}}} \right)\) với \(t \ge 1\). Xem \(y = S\left( t \right)\) là một hàm số xác định trên nửa khoảng \(\left[ {1; + \infty } \right)\), biết rằng tiệm cận ngang của đồ thị hàm số có dạng \(\frac{a}{b}\,,\,a\,,\,b \in {\mathbb{N}^*}\,,\,\left( {a\,,\,b} \right) = 1\). Tính \(P = a - 2b\).