10 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Giá trị nhỏ nhất của hàm sốcó bảng biến thiên sau trên khoảng \(\left[ { - 2;3} \right]\) là:
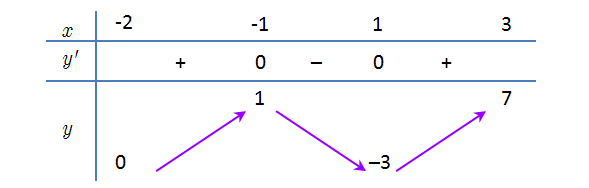
\[\mathop {\min }\limits_{\left[ { - 2;3} \right]} y = 0\].
\[\mathop {\min }\limits_{\left[ { - 2;3} \right]} y = - 3\].
\[\mathop {\min }\limits_{\left[ { - 2;3} \right]} y = 1\].
\[\mathop {\min }\limits_{\left[ { - 2;3} \right]} y = 7\].
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 5;\,3} \right)\) và có bảng biến thiên như sau
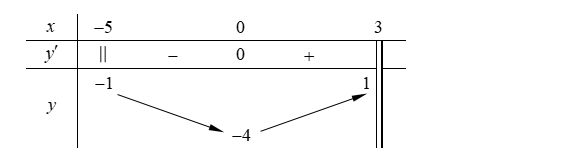
Mệnh đề nào sau đây đúng?
Hàm số \(y = f\left( x \right)\) không có giá trị nhỏ nhất và không có giá trị lớn nhất trên \(\left[ { - 5;\,3} \right)\).
Hàm số \(y = f\left( x \right)\) không có giá trị nhỏ nhất và có giá trị lớn nhất trên \(\left[ { - 5;\,3} \right)\).
Hàm số \(y = f\left( x \right)\) có giá trị nhỏ nhất và có giá trị lớn nhất trên \(\left[ { - 5;\,3} \right)\).
Hàm số có giá trị nhỏ nhất và không có giá trị lớn nhất trên \(\left[ { - 5;\,3} \right)\).
Cho hàm số \(y = f\left( x \right)\) liên tục và có bảng biến thiên trong đoạn \(\left[ { - 2;\,4} \right]\) như sau
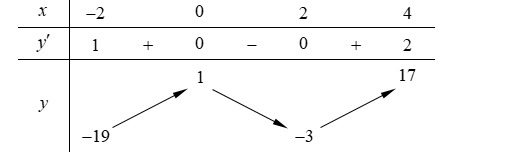
Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 2;\,4} \right]\) bằng
\[ - 19\].
1.
\[ - 3\].
\[17\].
Giá trị nhỏ nhất trên tập xác định của hàm số có đồ thị sau là:
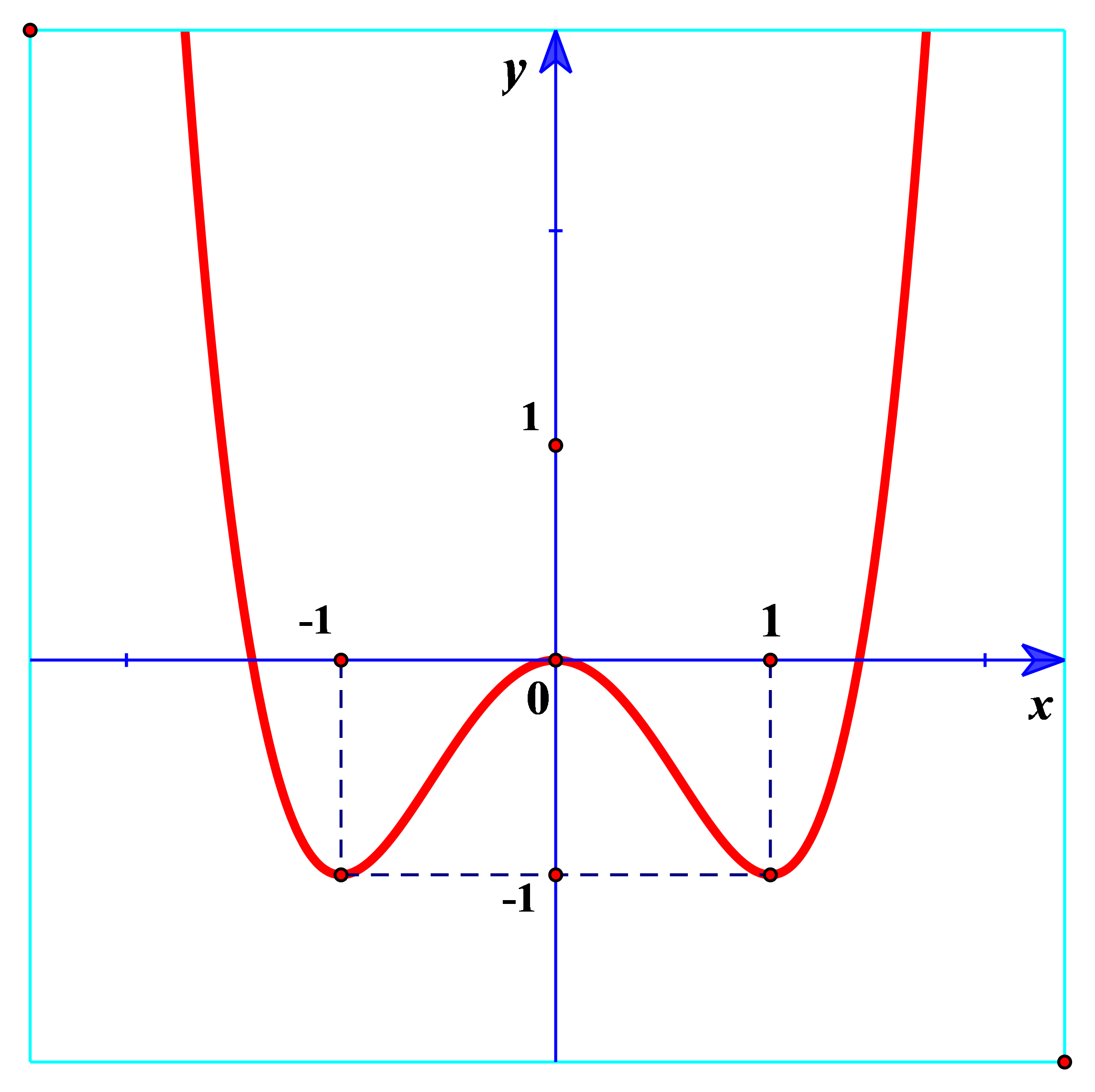
\[\mathop {\min }\limits_{} y = - 1.\]
\[\mathop {\min }\limits_{} y = 1\].
\[\mathop {\min }\limits_{} y = 0\].
\[\mathop {\min }\limits_{} y = - 2\].
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y = {x^3} - 3{x^2} - 9x + 2\] trên \[\left[ { - 2;\,2} \right]\] lần lượt là:
7 và 2.
7 và \[ - 1\].
7 và 0.
7 và \[ - 20\].
Giá trị nhỏ nhất của hàm \(y = {e^{{x^2} - 2x}}\) trên đoạn \(\left[ {0;2} \right]\) là
\(\mathop {\min y}\limits_{\left[ {0;2} \right]} = 1\).
\(\mathop {\min y}\limits_{\left[ {0;2} \right]} = e\).
\(\mathop {\min y}\limits_{\left[ {0;2} \right]} = \frac{1}{{{e^2}}}\).
\(\mathop {\min y}\limits_{\left[ {0;2} \right]} = \frac{1}{e}\).
Gọi giá trị lớn nhất, nhỏ nhất của hàm số \[y = x - 5 + \frac{1}{x}\] trên khoảng \[\left( {0; + \infty } \right)\] là \[M;m\]. Khi đó, các giá trị \[M;m\]lần lượt là :
Không có \(M\); \[m = - 3\].
\[M = - 3\]; \[m = 1\].
\[M = 0\]; \[m = 1\].
Không có \[M;m\].
Cho đồ thị hàm số \(y = f'(x)\) như hình vẽ.
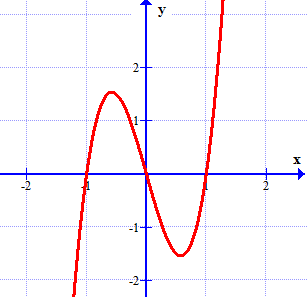
Hàm số \(y = f(x)\) đạt giá trị nhỏ nhất trên khoảng \(\left[ {0;2} \right]\) tại \[x\] bằng bao nhiêu?
\[x = \frac{2}{3}\].
\[x = 0\].
\[x = 1\].
\[x = 2\].
Cho đồ thị hàm số \(y = f'(x)\) như hình vẽ.
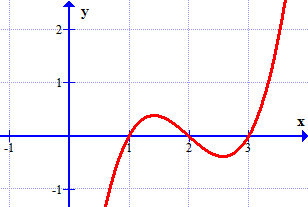
Hàm số \(y = f(x)\) đạt giá trị lớn nhất trên khoảng \(\left[ {1;3} \right]\) tại \[{x_0}\]. Khi đó giá trị của \[x_0^2 - 2{x_0} + 2018\] bằng bao nhiêu?
\[2018\].
\[2017\].
\[2021\].
\[2026\].
Một chất điểm chuyển động theo quy luật \(s\left( t \right) = {t^2} - \frac{1}{6}{t^3}\left( {\rm{m}} \right).\) Tìm thời điểm \(t\) (giây) mà tại đó vận tốc \(v\left( {{\rm{m/s}}} \right)\) của chuyển động đạt giá trị lớn nhất.
\(t = 2\).
\(t = 0,5\).
\(t = 2,5\).
\(t = 1\).
