10 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Tìm khoảng đồng biến của hàm số: \[y = - {x^4} + 4{x^2} - 3\].
\((0; + \infty )\).
\(( - \infty ;0)\).
\(( - \infty ; - \sqrt 2 )\)và \((0;\sqrt 2 )\).
\((\sqrt 2 ; + \infty )\).
Tìm khoảng nghịch biến của hàm số: \[y = \frac{{3 - 2x}}{{x + 7}}\].
\(( - \infty ;7)\).
\(( - \infty ; + \infty )\).
\(( - \infty ; - 7)\)và \(( - 7; + \infty )\).
\(( - 10; + \infty )\).
Hàm số \(y = \sqrt {2x - {x^2}} \) nghịch biến trên khoảng nào.
\(\left( {0;1} \right)\).
\(\left( { - \infty ;1} \right)\).
\(\left( {1;2} \right)\).
\(\left( {1; + \infty } \right)\).
Hàm số nào sau đây đồng biến trên \(\mathbb{R}\)?
\[y = \frac{{x - 1}}{{x + 2}}\].
\[y = {x^3} + 4{x^2} + 3x--1\].
\[y = {x^4}--2{x^2}--1\].
\[y = \frac{1}{3}{x^3} - \frac{1}{2}{x^2} + 3x + 1\].
Cho các hàm số sau:
\(\left( I \right):y = - {x^3} + 3{x^2} - 3x + 1;\left( {II} \right):y = \sin x - 2x;\)\(\left( {III} \right):y = - \sqrt {{x^3} + 2} ;\left( {IV} \right):y = \frac{{x - 2}}{{1 - x}}\).
Hỏi hàm số nào nghịch biến trên toàn trục số?
(I), (II).
(I), (II) và (III).
(I), (II) và (IV).
(II), (III).
Cho hàm số \[y = f\left( x \right)\] xác định và liên tục trên R và có đồ thị là đường cong trong hình vẽ bên. Hỏi điểm cực tiểu của đồ thị hàm số \[y = f\left( x \right)\]là điểm nào?
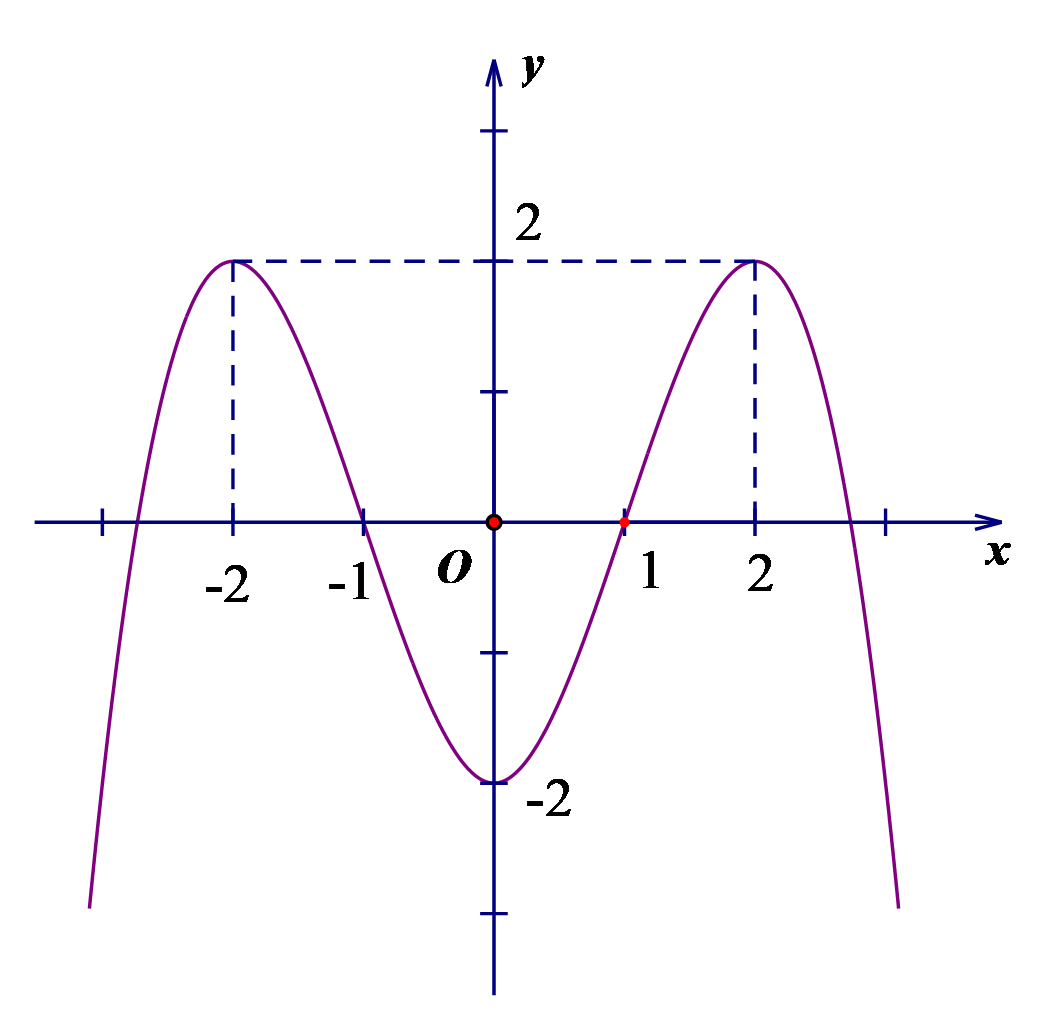
\[x = - 2.\]
\[y = - 2.\]
\[M\left( {0; - 2} \right).\]
\[N\left( {2\,;2} \right).\]
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {0;4} \right]\) có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?
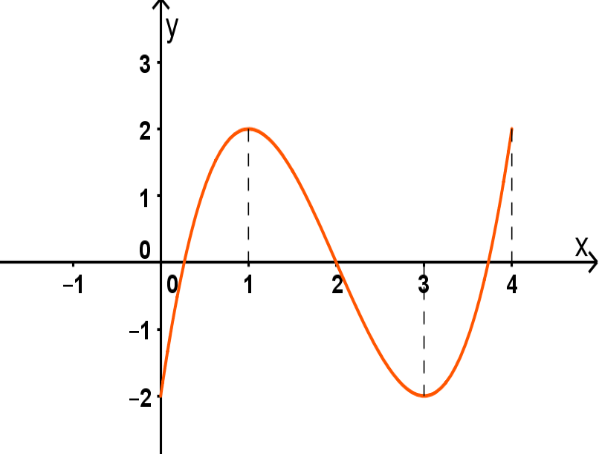
Hàm số đạt cực đại tại \(x = 4.\)
Hàm số đạt cực tiểu tại \(x = 0.\)
Hàm số đạt cực đại tại \(x = 2.\)
Hàm số đạt cực tiểu tại \(x = 3.\)
Gọi \(M,n\) lần lượt là giá trị cực đại, giá trị cực tiểu của hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\) . Khi đó giá trị của biểu thức \({M^2} - 2n\) bằng:
8.
7.
9.
6.
Hàm số nào sau đây không có cực trị?
\(y = 2x + \frac{2}{{x + 1}}.\)
\(y = {x^3} + 3{x^2}.\)
\(y = - {x^4} + 2{x^2} + 3.\)
\(y = \frac{{x + 1}}{{x - 2}}.\)
Cho hàm số \(y = f(x)\)có bảng biến thiên như sau:
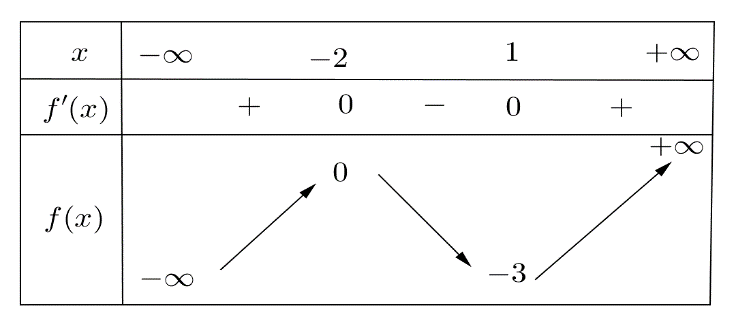
Giá trị cực tiểu của hàm số đã cho là:
\( - 2\).
\(1\).
\( - 3\) .
\(0\).
