7 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Tập xác định hàm số \(y = \sin x\) là:
\(D = {\rm{[}} - 1;1].\)
\(D = \mathbb{R}.\)
\(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}.\)
\(D = \mathbb{R}\backslash \left\{ {k\frac{\pi }{2},k \in \mathbb{Z}} \right\}.\)
Mệnh đề nào sau đây là đúng?
Hàm số \(y = \sin x\) là hàm số chẵn.
Hàm số \[y = \cos x\] là hàm số chẵn.
Hàm số \(y = \tan x\)là hàm số chẵn.
Hàm số \(y = \cot x\) là hàm số chẵn.
Cho hàm số \(y = f(x)\) có đồ thị như hình bên dưới. Mệnh đề nào sau đây là đúng?
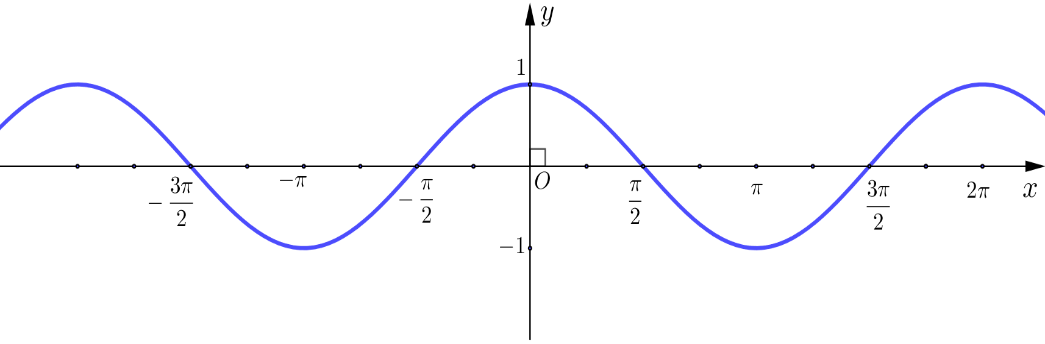
Hàm số đồng biến trên \[\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right).\]
Hàm số đồng biến trên \[\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right).\]
Hàm số đồng biến trên \[\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right).\]
Hàm số đồng biến trên \[\left( { - \frac{\pi }{2};0} \right).\]
Tìm tập xác định của hàm số \(y = \tan x\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi \,|k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {k\pi \,|k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi \,|k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {k2\pi \,|k \in \mathbb{Z}} \right\}\).
Tìm tập xác định của hàm số \(y = \cot \left( {2x - \frac{\pi }{3}} \right)\).
\(\mathbb{R}\backslash \left\{ {\frac{{2\pi }}{3} + k\frac{\pi }{2}\,|k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{6} + k\pi \,|k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {\frac{{2\pi }}{3} + k\pi \,|k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{6} + k\frac{\pi }{2}\,|k \in \mathbb{Z}} \right\}\).
Tập giá trị của hàm số \(y = 2\sin x\) là
\[\left[ { - 1;1} \right]\].
\[\left[ {0;2} \right]\].
\[\left\{ { - 2;2} \right\}\].
\[\left[ { - 2;2} \right]\].
Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?

\[y = \tan x\].
\(y = \sin x\).
\[y = \cot x\].
\(y = \cos x\).
