15 CÂU HỎI
Một trong bốn đường thẳng dưới đây là đường tiệm cận ngang của đồ thị hàm số ở Hình 1. Hỏi đường tiệm cận ngang của đồ thị hàm số đó là đường nào?
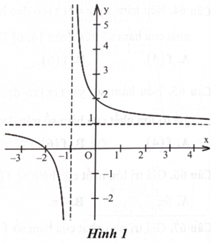
A. \(x = - 1.\)
B. \(x = - 2.\)
C. \({\rm{y}} = 1.\)
D. \({\rm{y}} = 2.\)
Một trong bốn đường thẳng dưới đây là đường tiệm cận đứng của đồ thị hàm số ở Hình 1. Hỏi đường tiệm cận đứng của đồ thị hàm số đó là đường nào?
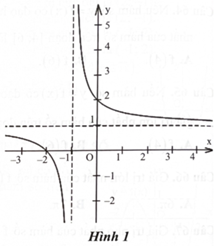
A. \({\rm{x}} = - 1.\)
B. \({\rm{x}} = - 2.\)
C. \({\rm{y}} = 1.\)
D. \({\rm{y}} = 2.\)
Một trong bốn đường thẳng dưới đây là đường tiệm cận xiên của đồ thị hàm số ở Hình 2. Hỏi đường tiệm cận xiên của đồ thị hàm số đó là đường nào?
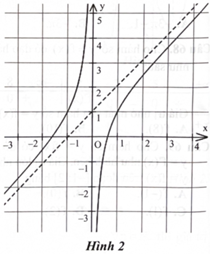
A. \(y = x.\)
B. \({\rm{y}} = {\rm{x}} + 1.\)
C. \(y = - x + 1.\)
D. \(y = 2x + 1.\)
Cho hàm số \(y = f(x)\) có \(\mathop {\lim }\limits_{x \to 3} f(x) = + \infty ,\mathop {\lim }\limits_{x \to - \infty } f(x) = - 3.\) Phát biểu nào sau đây là đúng?
A. Đồ thị hàm số có tiệm cận ngang là đường thẳng \({\rm{y}} = 3\) và tiệm cận đứng là đường thẳng \({\rm{x}} = - 3.\)
B. Đồ thị hàm số có tiệm cận ngang là đường thẳng \(x = 3\) và tiệm cận đứng là đường thẳng \({\rm{y}} = - 3.\)
C. Đồ thị hàm số có tiệm cận ngang là đường thẳng \(x = - 3\) và tiệm cận đứng là đường thẳng \({\rm{y}} = 3.\)
D. Đồ thị hàm số có tiệm cận ngang là đường thẳng \({\rm{y}} = - 3\) và tiệm cận đứng là đường thẳng \({\rm{x}} = 3.\)
Cho hàm số \(y = f(x)\) thoả mãn \(\mathop {\lim }\limits_{x \to - \infty } [f(x) - 5x + 7] = 0.\) Đường tiệm cận xiên của đồ thị hàm số \(y = f(x)\) là
A. \({\rm{y}} = 5{\rm{x}} - 7.\)
B. \({\rm{y}} = 5{\rm{x}} + 7.\)
C. \(y = - 5x - 7.\)
D. \(y = 5x + 7.\)
Cho hàm số phù hợp với bảng biến thiên sau:
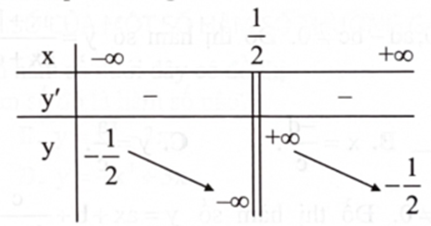
Phát biểu nào sau đây là đúng?
A. Đồ thị hàm số có đường tiệm cận ngang là \({\rm{y}} = \frac{{ - 1}}{2}\), đường tiệm cận đứng là \({\rm{x}} = \frac{1}{2}.\)
B. Đồ thị hàm số có đường tiệm cận ngang là \({\rm{y}} = \frac{1}{2}\), đường tiệm cận đứng là \(x = \frac{{ - 1}}{2}.\)
C. Đồ thị hàm số chỉ có đúng một đường tiệm cận, đó là \({\rm{y}} = \frac{{ - 1}}{2}.\)
D. Đồ thị hàm số chỉ có đúng một đường tiệm cận, đó là \(x = \frac{1}{2}.\)
Cho hàm số phù hợp với bảng biến thiên sau:
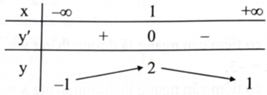
Phát biểu nào sau đây là đúng?
A. Đồ thị hàm số có hai đường tiệm cận ngang là \({\rm{y}} = - 1,{\rm{y}} = 1.\)
B. Đồ thị hàm số có hai đường tiệm cận ngang là \({\rm{x}} = - 1,{\rm{x}} = 1.\)
C. Đồ thị hàm số không có đường tiệm cận ngang.
D. Đồ thị hàm số có đường tiệm cận đứng.
Cho \({\rm{ac}} \ne 0,{\rm{ad}} - {\rm{bc}} \ne 0.\) Đồ thị hàm số \({\rm{y}} = \frac{{{\rm{ax}} + {\rm{b}}}}{{{\rm{cx}} + {\rm{d}}}}\) có đường tiệm cận ngang là
A. \({\rm{x}} = \frac{{\rm{a}}}{{\rm{c}}}.\)
B. \(x = \frac{{ - d}}{c}.\)
C. \({\rm{y}} = \frac{{\rm{a}}}{{\rm{c}}}.\)
D. \(y = \frac{{ - d}}{c}.\)
Cho \({\rm{ac}} \ne 0,{\rm{ad}} - {\rm{bc}} \ne 0.\) Đồ thị hàm số \({\rm{y}} = \frac{{{\rm{ax}} + {\rm{b}}}}{{{\rm{cx}} + {\rm{d}}}}\) có đường tiệm cận đứng là
A. \({\rm{x}} = \frac{{\rm{a}}}{{\rm{c}}}.\)
B. \(x = \frac{{ - d}}{c}.\)
C. \({\rm{y}} = \frac{{\rm{a}}}{{\rm{c}}}.\)
D. \({\rm{y}} = \frac{{ - {\rm{d}}}}{{\rm{c}}}.\)
Cho \({\rm{acd}} \ne 0.\) Đồ thị hàm số \({\rm{y}} = {\rm{ax}} + {\rm{b}} + \frac{{\rm{c}}}{{{\rm{dx}} + {\rm{e}}}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{d}},{\rm{e}} \in \mathbb{R})\) có đường tiệm cận xiên là
A. \(y = ax + b.\)
B. \(y = dx + e.\)
C. \(y = bx + a.\)
D. \(y = ex + d.\)
Đồ thị hàm số \(y = \frac{{x - 1}}{{x + 1}}\) có:
A. Tiệm cận ngang là đường thẳng \({\rm{y}} = 1\) và tiệm cận đứng là đường thẳng \({\rm{x}} = 1.\)
B. Tiệm cận ngang là đường thẳng \({\rm{y}} = 1\) và tiệm cận đứng là đường thẳng \(x = - 1.\)
C. Tiệm cận ngang là đường thẳng \({\rm{y}} = - 1\) và tiệm cận đứng là đường thẳng \({\rm{x}} = 1.\)
D. Tiệm cận ngang là đường thẳng \({\rm{y}} = - 1\) và tiệm cận đứng là đường thẳng \({\rm{x}} = - 1.\)
Cho đường thẳng \({\rm{y}} = {\rm{ax}} + {\rm{b}}({\rm{a}},{\rm{b}} \in \mathbb{R})\) là đường tiệm cận xiên của đồ thị hàm số \({\rm{y}} = \frac{{ - 3{{\rm{x}}^2} + 5{\rm{x}} + 1}}{{2{\rm{x}} + 1}}.\) Giá trị của a là
A. \(\frac{3}{2}.\)
B. \(\frac{{ - 3}}{2}.\)
C. \(\frac{2}{3}.\)
D. \(\frac{{ - 2}}{3}.\)
Cho đường thẳng \({\rm{y}} = {\rm{ax}} + {\rm{b}}({\rm{a}},{\rm{b}} \in \mathbb{R})\) là đường tiệm cận xiên của đồ thị hàm số \({\rm{y}} = \sqrt {9{{\rm{x}}^2} + 1} .\) Tập hợp các giá trị của a là
A. \(\{ 3\} .\)
B. \(\{ - 3\} .\)
C. \(\{ - 3;3\} .\)
D. \(\{ 9\} .\)
Số đường tiệm cận đứng của đồ thị hàm số \({\rm{y}} = \frac{{\sin {\rm{x}}}}{{\rm{x}}}\) là
A. 0.
B. 1.
C. 2.
D. 3.
Số đường tiệm cận đứng của đồ thị hàm số \({\rm{y}} = \frac{{{{\rm{e}}^{\rm{x}}} - 1}}{{\rm{x}}}\) là
A. 0.
B. 1.
C. 2.
D. 3.
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
