13 CÂU HỎI
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có đồ thị như Hình 1. Giá trị nhỏ nhất của hàm số trên đoạn \([ - 2;2]\) là
![Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có đồ thị như Hình 1. Giá trị nhỏ nhất của hàm số trên đoạn \([ - 2;2]\) là A. -2. B. -1. C. 1. D. -3. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid0-1726996503.png)
A. -2.
B. -1.
C. 1.
D. -3.
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có đồ thị như Hình 1. Giá trị lớn nhất của hàm số trên đoạn \([ - 2;2]\) là
![Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có đồ thị như Hình 1. Giá trị lớn nhất của hàm số trên đoạn \([ - 2;2]\) là A. 2. B. -1. C. 1. D. -3. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid1-1726996562.png)
A. 2.
B. -1.
C. 1.
D. -3.
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như Hình 2. Giá trị lớn nhất của hàm số trên khoảng \(( - \infty ;5)\) là
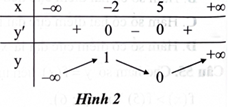
A. 0.
B. 1.
C. -2.
D. 5.
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như Hình 2. Giá trị nhỏ nhất của hàm số trên khoảng \(( - 2; + \infty )\) là
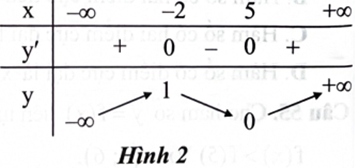
A. 0.
B. 1.
C. -2.
D. 5.
Nếu hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đạo hàm \({{\rm{f}}^\prime }({\rm{x}}) = 6 - \frac{1}{{\sqrt {{{\rm{x}}^2} + 1} }}\forall {\rm{x}} \in \mathbb{R}\) thì giá trị nhỏ nhất của hàm số trên đoạn [4; 6] là
A. \({\rm{f}}(4).\)
B. \({\rm{f}}(6).\)
C. \({\rm{f}}(5).\)
D. \({\rm{f}}(\sqrt {24} ).\)
Nếu hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đạo hàm \({{\rm{f}}^\prime }({\rm{x}}) = \frac{1}{{\sqrt {{{\rm{x}}^2} + 2} }} - 1\forall {\rm{x}} \in \mathbb{R}\) thì giá trị nhỏ nhất của hàm số trên đoạn [4; 6] là
A. \(f(4).\)
B. \({\rm{f}}(6).\)
C. \({\rm{f}}(5).\)
D. \({\rm{f}}(\sqrt {24} ).\)
Nếu hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đạo hàm \({{\rm{f}}^\prime }({\rm{x}}) = 2 - \frac{{2{\rm{x}}}}{{{{\rm{x}}^2} + 1}}\forall {\rm{x}} \in \mathbb{R}\) thì giá trị lớn nhất của hàm số trên đoạn [4; 6] là
A. \(f(4).\)
B. \({\rm{f}}(6).\)
C. \({\rm{f}}(5).\)
D. \({\rm{f}}(\sqrt {24} ).\)
Nếu hàm số \(y = f(x)\) có đạo hàm \({{\rm{f}}^\prime }({\rm{x}}) = - \sin {\rm{x}}\cos {\rm{x}} - \frac{1}{{\sqrt 2 }}\forall {\rm{x}} \in \mathbb{R}\) thì giá trị lớn nhất của hàm số trên đoạn [4; 6] là
A. \({\rm{f}}(4).\)
B. \({\rm{f}}(6).\)
C. \({\rm{f}}(5).\)
D. \({\rm{f}}(\sqrt {24} ).\)
Giá trị lớn nhất của hàm số \({\rm{f}}({\rm{x}}) = 3{\rm{x}} + \sin \frac{{\rm{x}}}{2}\) trên đoạn \([0;2\pi ]\) là
A. \(6\pi .\)
B. \(7\pi .\)
C. \(8\pi .\)
D. \(9\pi .\)
Giá trị nhỏ nhất của hàm số \({\rm{f}}({\rm{x}}) = 2{\rm{x}} - \cos \frac{{\rm{x}}}{2}\) trên đoạn \(\left[ {\frac{{ - 3\pi }}{2};\pi } \right]\) là
A. \( - 3\pi - 1.\)
B. \( - 3\pi .\)
C. \( - 3\pi + \frac{{\sqrt 2 }}{2}.\)
D. \( - 3\pi - \frac{{\sqrt 2 }}{2}.\)
Cho hàm số \(y = f(x)\) có đạo hàm trên \(\mathbb{R}\) và có bảng xét dấu của đạo hàm như sau:
![Cho hàm số \(y = f(x)\) có đạo hàm trên \(\mathbb{R}\) và có bảng xét dấu của đạo hàm như sau: Giá trị nhỏ nhất của hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) trên đoạn [8; 12] bằng A. \({\rm{f}}(8).\) B. \({\rm{f}}(10).\) C. \({\rm{f}}(11).\) D. \({\rm{f}}(12).\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid4-1726997076.png)
Giá trị nhỏ nhất của hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) trên đoạn [8; 12] bằng
A. \({\rm{f}}(8).\)
B. \({\rm{f}}(10).\)
C. \({\rm{f}}(11).\)
D. \({\rm{f}}(12).\)
Cho hàm số \(y = f(x)\) có đồ thị đạo hàm \({\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})\) như hình bên. Giá trị lớn nhất của hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) trên đoạn \([ - 1;2]\) bằng
![Cho hàm số \(y = f(x)\) có đồ thị đạo hàm \({\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})\) như hình bên. Giá trị lớn nhất của hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) trên đoạn \([ - 1;2]\) bằng A. \(f( - 1).\) B. \({\rm{f}}(0).\) C. \({\rm{f}}(1).\) D. \({\rm{f}}(2).\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid5-1726997136.png)
A. \(f( - 1).\)
B. \({\rm{f}}(0).\)
C. \({\rm{f}}(1).\)
D. \({\rm{f}}(2).\)
Nếu hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) thoả mãn \(f(x) \le f(1)\forall x \in \mathbb{R}\) thì
A. Hàm số đạt cực đại tại \({{\rm{x}}_0} = 1.\)
B. Hàm số đạt cực tiểu tại \({x_0} = 1.\)
C. Hàm số đạt giá trị nhỏ nhất bằng \({\rm{f}}(1).\)
D. Hàm số đạt giá trị lớn nhất bằng \({\rm{f}}(1).\)
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải