17 câu hỏi
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đồ thị như Hình 1. Điểm cực tiểu của hàm số đã cho là
-1.
1.
0.
4.
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đồ thị như Hình 1. Điểm cực đại của hàm số đã cho là
-1.
1.
0.
4.
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đồ thị như Hình 1. Giá trị cực tiểu của hàm số đã cho là
-1.
1.
0.
4.
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đồ thị như Hình 1. Giá trị cực đại của hàm số đã cho là
-1.
1.
0.
4.
Cho hàm số có bảng biến thiên như Hình 2. Điểm cực tiểu của hàm số đã cho là
-2.
-1.
0.
3.
Cho hàm số có bảng biến thiên như Hình 2. Điểm cực đại của hàm số đã cho là
-2.
-1.
0.
3.
Cho hàm số có bảng biến thiên như Hình 2. Giá trị cực tiểu của hàm số đã cho là
-2.
-1.
0.
3.
Cho hàm số có bảng biến thiên như Hình 2. Giá trị cực đại của hàm số đã cho là
-2.
-1.
0.
3.
Cho hàm số \(y = f(x)\) có đạo hàm trên \(\mathbb{R}\) và có bảng xét dấu của đạo hàm như sau:
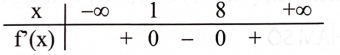
Phát biểu nào sau đây là đúng?
Hàm số có điểm cực tiểu là \({x_1} = 1\) và có điểm cực đại là \({x_2} = 8.\)
Hàm số có điểm cực đại là \({x_1} = 1\) và có điểm cực tiểu là \({x_2} = 8.\)
Hàm số có hai điểm cực tiểu là \({{\rm{x}}_1} = 1\) và \({{\rm{x}}_2} = 8.\)
Hàm số có hai điểm cực đại là \({{\rm{x}}_1} = 1\) và \({{\rm{x}}_2} = 8.\)
Cho hàm số có đạo hàm trên có bảng xét dấu của đạo hàm như sau:
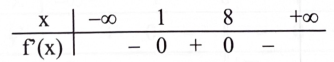
Phát biểu nào sau đây là đúng?
Hàm số có điểm cực tiểu là \({x_1} = 1\) và có điểm cực đại là \({x_2} = 8.\)
Hàm số có hai điểm cực tiểu là \({x_1} = 1\) và \({x_2} = 8.\)
Hàm số có hai điểm cực đại là \({x_1} = 1\) và \({x_2} = 8.\)
Hàm số có điểm cực đại là \({x_1} = 1\) và có điểm cực tiểu là \({x_2} = 8.\)
Cho hàm số \(y = f(x)\) có đạo hàm trên \(\mathbb{R}\) và có bảng xét dấu của đạo hàm như sau:
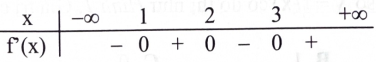
Phát biểu nào sau đây là đúng?
Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) không có điểm cực tiểu.
Hàm số \(y = f(x)\) có đúng một điểm cực tiểu.
Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đúng hai điểm cực tiểu.
Hàm số \(y = f(x)\) có đúng ba điểm cực tiểu.
Cho hàm số \(y = f(x)\) có đạo hàm trên \(\mathbb{R}\) và có bảng xét dấu của đạo hàm như sau:
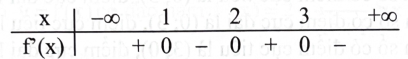
Phát biểu nào sau đây là đúng?
Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) không có điểm cực tiểu.
Hàm số \(y = f(x)\) có đúng một điểm cực tiểu.
Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đúng hai điểm cực tiểu.
Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đúng ba điểm cực tiểu.
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đạo hàm \({{\rm{f}}^\prime }({\rm{x}}) = {{\rm{x}}^2} - {\rm{x}} - 2.\) Phát biểu nào sau đây là đúng?
Hàm số có điểm cực tiểu là \({x_1} = - 1\) và có điểm cực đại là \({x_2} = 2.\)
Hàm số có hai điểm cực tiểu là \({{\rm{x}}_1} = - 1\) và \({{\rm{x}}_2} = 2.\)
Hàm số có hai điểm cực đại là \({x_1} = - 1\) và \({x_2} = 2.\)
Hàm số có điểm cực đại là \({x_1} = - 1\) và có điểm cực tiểu là \({x_2} = 2.\)
Cho hàm số có đạo hàm Phát biểu nào sau đây là đúng?
Hàm số có điểm cực tiểu là \({{\rm{x}}_1} = - 2\) và có điểm cực đại là \({{\rm{x}}_2} = 3.\)
Hàm số có hai điểm cực tiểu là \({{\rm{x}}_1} = - 2\) và \({{\rm{x}}_2} = 3.\)
Hàm số có hai điểm cực đại là \({x_1} = - 2\) và \({x_2} = 3.\)
Hàm số có điểm cực đại là \({x_1} = - 2\) và có điểm cực tiểu là \({x_2} = 3.\)
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) thoả mãn \(f(x) < f(0)\forall x \in ( - 1;1)\) và \({\rm{f}}({\rm{x}}) > {\rm{f}}(5)\forall {\rm{x}} \in (4;6).\) Phát biểu nào sau đây là đúng?
Hàm số có điểm cực tiểu là \({{\rm{x}}_1} = 0\) và có điểm cực đại là \({{\rm{x}}_2} = 5.\)
Hàm số có hai điểm cực tiểu là \({x_1} = 0\) và \({x_2} = 5.\)
Hàm số có hai điểm cực đại là \({{\rm{x}}_1} = 0\) và \({{\rm{x}}_2} = 5.\)
Hàm số có điểm cực đại là \({x_1} = 0\) và có điểm cực tiểu là \({x_2} = 5.\)
Cho hàm số có đạo hàm trên \(\mathbb{R}\) và có bảng biến thiên như sau:
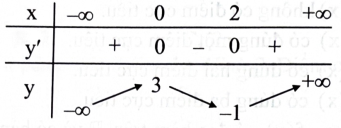
Phát biểu nào sau đây là đúng?
Đồ thị hàm số có điểm cực tiểu là \((0;3)\), điểm cực đại là \((2; - 1).\)
Đồ thị hàm số có điểm cực đại là \((0;3)\), điểm cực tiểu là \((2; - 1).\)
Đồ thị hàm số có điểm cực tiểu là \((3;0)\), điểm cực đại là \(( - 1;2).\)
Đồ thị hàm số có điểm cực đại là \((3;0)\), điểm cực tiểu là \(( - 1;2).\)
Cho hàm số \(y = a{x^4} + b{x^3} + c{x^2} + dx + e(a,b,c,d,e \in \mathbb{R})\) có đồ thị như hình bên. Số điểm cực trị của hàm số là
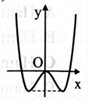
0.
1.
2.
3.
Gợi ý cho bạn
Xem tất cảCÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
CÂU TRẮC NGHIỆM ĐÚNG SAI
DẠNG 8. ĐỒ THỊ HÀM SỐ CỦA MỘT SỐ HÀM SỐ THƯỜNG GẶP
DẠNG 7. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
DẠNG 6. GIÁ TRỊ NHỎ NHẤT, GIÁ TRỊ LỚN NHẤT CỦA HÀM SỐ
DẠNG 4. SỰ BIẾN THIÊN CỦA HÀM SỐ
DẠNG 3. Ý NGHĨA VẬT LÍ CỦA ĐẠO HÀM