15 câu hỏi
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đồ thị như Hình 1. Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) đồng biến trên khoảng
\(( - 1;0).\)
\((0;1).\)
\((1;3).\)
\(( - 2; - 1).\)
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đồ thị đạo hàm \(y = {f^\prime }(x)\) như Hình 1. Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) đồng biến trên khoảng
\(( - 2;0).\)
\((0;2).\)
\((1;3).\)
\((3;4).\)
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đồ thị như Hình 1. Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) nghịch biến trên khoảng
\(( - 1;0).\)
\((0;1).\)
\((1;3).\)
\(( - 1;1).\)
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đồ thị đạo hàm \({\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})\) như Hình 1. Hàm số \(y = f(x)\) nghịch biến trên khoảng
\(( - 2; - 1).\)
\((1;2).\)
\((2;3).\)
\(( - 1;1).\)
Cho hàm số \({\rm{y}} = \frac{{{\rm{ax}} + {\rm{b}}}}{{{\rm{cx}} + {\rm{d}}}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{d}} \in \mathbb{R})\) có đồ thị như Hình 2. Phát biểu nào sau đây là đúng?
Hàm số đồng biến trên tập xác định.
Hàm số nghịch biến trên tập xác định.
Hàm số đồng biến trên từng khoảng xác định.
Hàm số nghịch biến trên từng khoảng xác định.
Cho hàm số \({\rm{y}} = \frac{{{\rm{a}}{{\rm{x}}^2} + {\rm{bx}} + {\rm{c}}}}{{{\rm{mx}} + {\rm{n}}}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{m}},{\rm{n}} \in \mathbb{R})\) có đồ thị như Hình 3. Phát biểu nào sau đây là đúng?
Hàm số đồng biến trên khoảng \(( - 2; - 1)\) và nghịch biến trên khoảng \((2;3).\)
Hàm số nghịch biến trên khoảng \(( - 2; - 1)\) và nghịch biến trên khoảng \((2;3).\)
Hàm số đồng biến trên khoảng \(( - 2; - 1)\) và đồng biến trên khoảng \((2;3).\)
Hàm số nghịch biến trên khoảng \(( - 2; - 1)\) và đồng biến trên khoảng \((2;3).\)
Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:
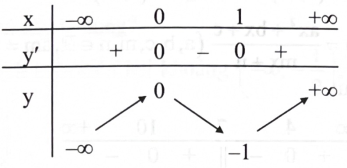Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) đồng biến trên khoảng
\(( - 1; + \infty ).\)
\(( - \infty ;1).\)
\((0;1).\)
\(( - 3; - 2).\)
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có bảng biến thiên như sau:
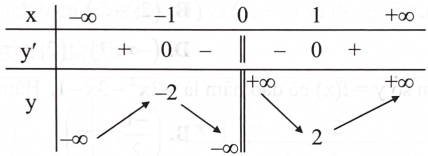
Hàm số nghịch biến trên khoảng
\(( - 1;1).\)
\(( - \infty ; - 2).\)
\((0;1).\)
\((2; + \infty ).\)
Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:
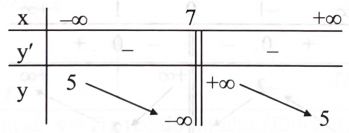Phát biểu nào sau đây là đúng?
Hàm số đồng biến trên khoảng \((5;6)\) và nghịch biến trên khoảng \((8;9).\)
Hàm số đồng biến trên khoảng \((5;6)\) và đồng biến trên khoảng \((8;9).\)
Hàm số nghịch biến trên khoảng \((5;6)\) và đồng biến trên khoảng \((8;9).\)
Hàm số nghịch biến trên khoảng \((5;6)\) và nghịch biến trên khoảng \((8;9).\)
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đạo hàm trên \(\mathbb{R}\) và có bảng xét dấu của đạo hàm như sau:
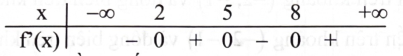Hàm số đã cho đồng biến trên khoảng
\(( - \infty ;2).\)
\((5;8).\)
\((3;4).\)
\((5; + \infty ).\)
Cho hàm số \({\rm{y}} = \frac{{{\rm{a}}{{\rm{x}}^2} + {\rm{bx}} + {\rm{c}}}}{{{\rm{mx}} + {\rm{n}}}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{m}},{\rm{n}} \in \mathbb{R},{\rm{am}} \ne 0)\) có bảng xét dấu của đạo hàm như sau:
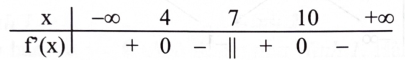
Hàm số đã cho nghịch biến trên khoảng
\((11;12).\)
\((7;10).\)
\(( - \infty ;7).\)
\((4; + \infty ).\)
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có đạo hàm là \({{\rm{x}}^2} - 3{\rm{x}} + 2.\) Hàm số nghịch biến trên
\(( - \infty ; - 1).\)
\((2; + \infty ).\)
\((1;2).\)
\(( - \infty ;1) \cup (2; + \infty ).\)
Cho hàm số \(y = f(x)\) có đạo hàm là \( - 2{x^2} - 3x - 1.\) Hàm số đồng biến trên
\(( - \infty ;1).\)
\(\left( {\frac{{ - 1}}{2}; + \infty } \right).\)
\(( - \infty ; - 1) \cup \left( {\frac{{ - 1}}{2}; + \infty } \right).\)
\(\left( { - 1;\frac{{ - 1}}{2}} \right).\)
Cho hàm số phù hợp với bảng biến thiên sau:
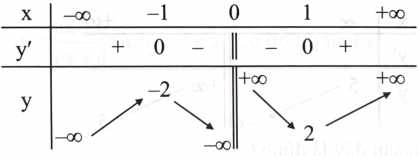
Phát biểu nào sau đây là đúng?
Hàm số đồng biến trên \(( - \infty ; - 1)\) và \((1; + \infty )\), nghịch biến trên \(( - 1;1).\)
Hàm số đồng biến trên \(( - \infty ; - 1)\) và \((1; + \infty )\), nghịch biến trên \(( - 1;0)\) và \((0;1).\)
Hàm số nghịch biến trên \(( - \infty ; - 1)\) và \((1; + \infty )\), đồng biến trên \(( - 1;1).\)
Hàm số đồng biến trên \(( - 1;0)\) và \((0;1)\), nghịch biến trên \(( - \infty ; - 1)\) và \((1; + \infty ).\)
Cho hàm số phù hợp với bảng biến thiên sau:
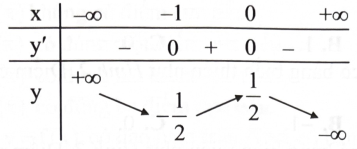
Phát biểu nào sau đây là đúng?
Hàm số nghịch biến trên hai khoảng \(\left( { - \infty ; - \frac{1}{2}} \right);\left( {\frac{1}{2}; + \infty } \right)\) và đồng biến trên \(\left( { - \frac{1}{2};\frac{1}{2}} \right).\)
Hàm số nghịch biến trên hai khoảng \(( - \infty ; - 1);(0; + \infty )\) và đồng biến trên \(( - 1;0).\)
Hàm số đồng biến trên hai khoảng \(( - \infty ; - 1);(1; + \infty )\) và nghịch biến trên \(( - 1;1).\)
Hàm số nghịch biến trên \(( - \infty ; - 1) \cup (1; + \infty )\) và đồng biến trên \(( - 1;1).\)
Gợi ý cho bạn
Xem tất cảCÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
CÂU TRẮC NGHIỆM ĐÚNG SAI
DẠNG 8. ĐỒ THỊ HÀM SỐ CỦA MỘT SỐ HÀM SỐ THƯỜNG GẶP
DẠNG 7. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
DẠNG 6. GIÁ TRỊ NHỎ NHẤT, GIÁ TRỊ LỚN NHẤT CỦA HÀM SỐ
DẠNG 5. CỰC TRỊ CỦA HÀM SỐ
DẠNG 3. Ý NGHĨA VẬT LÍ CỦA ĐẠO HÀM