30 CÂU HỎI
Thể tích của khối lập phương cạnh a là
A. \({\rm{V}} = {{\rm{a}}^3}.\)
B. \({\rm{V}} = \frac{1}{2}{{\rm{a}}^3}.\)
C. \({\rm{V}} = \frac{1}{3}{{\rm{a}}^3}.\)
D. \(V = 3{{\rm{a}}^3}.\)
Cho khối hộp chữ nhật \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) có \({\rm{AB}} = {\rm{a}},{\rm{AD}} = {\rm{b}},{\rm{A}}{{\rm{A}}^\prime } = {\rm{c}}.\) Thể tích của khối hộp chữ nhật \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) là
A. \({\rm{V}} = \frac{1}{3}{\rm{abc}}.\)
B. \({\rm{V}} = \frac{1}{2}{\rm{abc}}.\)
C. \({\rm{V}} = 3{\rm{abc}}.\)
D. \({\rm{V}} = {\rm{abc}}.\)
Công thức tính thể tích \(V\) của khối lăng trụ theo diện tích đáy \(B\) và chiều cao h là
A. \({\rm{V}} = \frac{1}{3}{\rm{Bh}}.\)
B. \({\rm{V}} = 3{\rm{Bh}}.\)
C. \({\rm{V}} = {\rm{Bh}}.\)
D. \({\rm{V}} = \frac{1}{2}{\rm{Bh}}.\)
Công thức tính thể tích V của khối chóp theo diện tích đáy B và chiều cao h là
A. \({\rm{V}} = \frac{1}{3}{\rm{Bh}}.\)
B. \({\rm{V}} = 3{\rm{Bh}}.\)
C. \({\rm{V}} = {\rm{Bh}}.\)
D. \({\rm{V}} = \frac{1}{2}{\rm{Bh}}.\)
Công thức tính thể tích V của khối chóp cụt đều theo diện tích hai đáy lần lượt là \({{\rm{S}}_1},\;{{\rm{S}}_2}\) và chiều cao h là
A. \({\rm{V}} = \frac{1}{3}\left( {\;{{\rm{S}}_1} - \sqrt {{{\rm{S}}_1}\;{{\rm{S}}_2}} + {{\rm{S}}_2}} \right){\rm{h}}.\)
B. \({\rm{V}} = \frac{1}{3}\left( {\;{{\rm{S}}_1} + \sqrt {{{\rm{S}}_1}\;{{\rm{S}}_2}} + {{\rm{S}}_2}} \right){\rm{h}}.\)
C. \({\rm{V}} = \frac{1}{3}\pi \left( {{{\rm{S}}_1} + \sqrt {{{\rm{S}}_1}\;{{\rm{S}}_2}} + {{\rm{S}}_2}} \right){\rm{h}}.\)
D. \({\rm{V}} = \frac{1}{3}\pi \left( {{{\rm{S}}_1} - \sqrt {{{\rm{S}}_1}\;{{\rm{S}}_2}} + {{\rm{S}}_2}} \right){\rm{h}}.\)
Nếu một khối lăng trụ có diện tích của đáy bằng \({{\rm{a}}^2}\) và có chiều cao bằng \(\frac{1}{2}\) a thì có thể tích bằng
A. \(3{{\rm{a}}^3}.\)
B. \({{\rm{a}}^3}.\)
C. \(\frac{1}{2}{{\rm{a}}^3}.\)
D. \(\frac{1}{3}{{\rm{a}}^3}.\)
Nếu một khối chóp có diện tích của đáy bằng \({{\rm{a}}^2}\) và có chiều cao bằng \(\frac{1}{3}\) a thì có thể tích bằng
A. \(3{a^3}.\)
B. \({{\rm{a}}^3}.\)
C. \(\frac{1}{9}{{\rm{a}}^3}.\)
D. \(\frac{1}{3}{{\rm{a}}^3}.\)
Nếu một khối lăng trụ tứ giác đều có cạnh đáy bằng 2 a và có chiều cao bằng 3 a thì có thể tích bằng
A. \(3{a^3}.\)
B. \(12{a^3}.\)
C. \(2{{\rm{a}}^3}.\)
D. \(4{a^3}.\)
Nếu một khối lăng trụ tam giác đều có cạnh đáy bằng 2 a và có chiều cao bằng 3 a thì có thể tích bằng
A. \(9{{\rm{a}}^3}.\)
B. \(3\sqrt 3 {a^3}.\)
C. \(3{a^3}.\)
D. \(\frac{{{{\rm{a}}^3}\sqrt 3 }}{4}\),
Nếu một khối chóp cụt tứ giác đều có cạnh đáy nhỏ và cạnh đáy lớn lần lượt bằng \(2{\rm{a}},3{\rm{a}}\) và có chiểu cao bằng 3 a thì có thể tích bằng
A. \(\frac{{19{{\rm{a}}^3}}}{3}.\)
B. \(19{{\rm{a}}^3}.\)
C. \(57{{\rm{a}}^3}.\)
D. \(13{{\rm{a}}^3}.\)
Cho khối chóp \({\rm{S}}.{\rm{ABC}}\) có diện tích tam giác ABC bằng \({\rm{S}},{\rm{SA}} = {\rm{a}}\), góc giữa SA và \(({\rm{ABC}})\) là \(\varphi .\) Thể tích của khối chóp \({\rm{S}}.{\rm{ABC}}\) là
A. \({\rm{V}} = \frac{1}{3}{\rm{Sa}}\cot \varphi .\)
B. \({\rm{V}} = \frac{1}{3}{\rm{Sa}}\cos \varphi .\)
C. \({\rm{V}} = \frac{1}{3}{\rm{Sa}}\sin \varphi .\)
D. \({\rm{V}} = \frac{1}{3}{\rm{Sa}}\tan \varphi .\)
Cho khối lăng trụ \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có ABCD là hình vuông cạnh a, \({\rm{A}}{{\rm{A}}^\prime } = {\rm{b}}\), góc giữa \({\rm{A}}{{\rm{A}}^\prime }\) và \(({\rm{ABCD}})\) là \(\varphi .\) Thể tích của khối lăng trụ ABCD.A'B'C'D' là
A. \(V = {a^2}b\sin \varphi .\)
B. \(V = {a^2}b\cos \varphi .\)
C. \(V = {{\rm{a}}^2}\;{\rm{b}}\cot \varphi .\)
D. \(V = \frac{1}{3}{{\rm{a}}^2}\;{\rm{b}}\sin \varphi .\)
Cho khối hộp chữ nhật \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }.\) Tỉ số thể tích của khối lăng trụ \({\rm{ABC}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }\) và khối hộp \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) là
A. \(\frac{1}{6}.\)
B. \(\frac{1}{3}.\)
C. \(\frac{1}{2}.\)
D. \(\frac{1}{4}.\)
Nếu tăng gấp 3 lần cạnh hình lập phương thì được hình lập phương mới có thể tích hơn thể tích hình lập phương ban đầu là \(208\;{\rm{c}}{{\rm{m}}^3}.\) Cạnh của hình lập phương ban đầu bằng
A. 8 cm.
B. 2 cm.
C. \(\sqrt[3]{{104}}\;{\rm{cm}}.\)
D. \(\sqrt[3]{{\frac{{208}}{7}}}\;{\rm{cm}}.\)
Khối hộp chữ nhật \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có \(AB = a,AD = a\sqrt 3 ,\quad A{C^\prime } = a\sqrt 6 \) có thể tích là
A. \(\frac{{{{\rm{a}}^3}\sqrt 6 }}{3}.\)
B. \(\frac{{2{{\rm{a}}^3}\sqrt 6 }}{3}.\)
C. \({a^3}\sqrt 6 .\)
D. \(3{a^3}\sqrt 2 .\)
Một hộp đựng thực phẩm có dạng hình lập phương và có diện tích toàn phần bằng \(150{\rm{d}}{{\rm{m}}^2}.\) Thể tích của khối hộp đó là
A. \(125\;{\rm{c}}{{\rm{m}}^3}.\)
B. \(125{\rm{d}}{{\rm{m}}^3}.\)
C. \(\frac{{125}}{3}\;{\rm{c}}{{\rm{m}}^3}.\)
D. \(\frac{{125}}{3}{\rm{d}}{{\rm{m}}^3}.\)
Một lăng kính có dạng hình lăng trụ đứng có đáy là tam giác vuông. Chiều cao của lăng kính là 10 cm, đáy của lăng kính là tam giác vuông có hai cạnh góc vuông lần lượt là 6 cm và 8 cm. Diện tích toàn phần của lăng kính là
A. \(288\;{\rm{c}}{{\rm{m}}^2}.\)
B. \(240\;{\rm{c}}{{\rm{m}}^2}.\)
C. \(336\;{\rm{c}}{{\rm{m}}^2}.\)
D. \(264\;{\rm{c}}{{\rm{m}}^2}.\)
Một viên gạch hình lăng trụ lục giác đều có chiều cao 8 cm , cạnh đáy 6 cm. Thể tích của viên gạch đó là
A. \(432\sqrt 3 \;{\rm{c}}{{\rm{m}}^3}.\)
B. \(144\sqrt 3 \;{\rm{c}}{{\rm{m}}^3}.\)
C. \(432\;{\rm{c}}{{\rm{m}}^3}.\)
D. \(144\;{\rm{c}}{{\rm{m}}^3}.\)
Một khúc gỗ có dạng hình lăng trụ tứ giác đều có cạnh đáy là 40 cm và chiều cao là 1 m. Mỗi mét khối gỗ này có giá 3 triệu đồng. Hỏi khúc gỗ đó có giá bao nhiêu tiền?
A. 1 triệu 600 nghìn đồng.
B. 480 nghìn đồng.
C. 48 triệu đồng.
D. 4 triệu 800 nghìn đồng.
Cho khối lăng trụ \({\rm{ABC}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }.\) Tỉ số thể tích của khối tứ diện \({{\rm{A}}^\prime }{\rm{ABC}}\) và khối lăng trụ \({\rm{ABC}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }\) là
A. \(\frac{1}{6}.\)
B. 3.
C. \(\frac{1}{2}.\)
D. \(\frac{1}{3}.\)
Cho khối hộp \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }.\) Tỉ số thể tích của khối tứ diện \({\rm{ABD}}{{\rm{A}}^\prime }\) và khối hộp \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) là
A. \(\frac{1}{3}.\)
B. \(\frac{1}{6}.\)
C. \(\frac{1}{2}.\)
D. \(\frac{1}{4}.\)
Cho hình chóp \({\rm{S}}.{\rm{ABCD}}\) có đáy ABCD là hình vuông cạnh \({\rm{a}},{\rm{SA}}\) vuông góc với \(({\rm{ABCD}})\), góc giữa đường thẳng SC và \(({\rm{ABCD}})\) là \({60^o }.\) Thể tích khối chóp $S. A B C D$ là
A. \(\frac{{{{\rm{a}}^3}\sqrt 3 }}{6}.\)
B. \(\frac{{{{\rm{a}}^3}\sqrt 6 }}{6}.\)
C. \(\frac{{{a^3}\sqrt 3 }}{3}.\)
D. \(\frac{{{{\rm{a}}^3}\sqrt 6 }}{3}.\)
Cho khối chóp đều \({\rm{S}}.{\rm{ABCD}}\) có tất cả các cạnh bằng a. Thể tích của khối chóp đều \({\rm{S}}.{\rm{ABCD}}\) là
A. \(\frac{{\sqrt 2 {a^3}}}{6}.\)
B. \(\frac{{{{\rm{a}}^3}}}{4}.\)
C. \(\sqrt 2 {a^3}.\)
D. \(\frac{{\sqrt 2 {{\rm{a}}^3}}}{{12}}.\)
Cho khối chóp đều \({\rm{S}}.{\rm{ABC}}\) có cạnh đáy bằng a , góc giữa đường thẳng SA và mặt phẳng \(({\rm{ABC}})\) bằng \({45^o }.\) Thể tích của khối chóp đều \({\rm{S}}.{\rm{ABC}}\) là
A. \(\frac{{\sqrt 2 {a^3}}}{{12}}.\)
B. \(\frac{{{{\rm{a}}^3}}}{{12}}.\)
C. \(\frac{{\sqrt 3 {{\rm{a}}^3}}}{{12}}.\)
D. \(\frac{{{{\rm{a}}^3}}}{4}.\)
Cho tứ diện đều ABCD cạnh a. Thể tích của khối tứ diện ABCD là
A. \({{\rm{a}}^3}.\)
B. \(\frac{{{{\rm{a}}^3}}}{3}.\)
C. \(\frac{{{{\rm{a}}^3}\sqrt 2 }}{{12}}.\)
D. \(\frac{{{a^3}\sqrt 2 }}{3}.\)
Cho khối lập phương \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) cạnh a. Thể tích của khối tứ diện \({\rm{AC}}{{\rm{B}}^\prime }{{\rm{D}}^\prime }\) là
A. \({{\rm{a}}^3}.\)
B. \(\frac{{{{\rm{a}}^3}}}{4}.\)
C. \(\frac{{{{\rm{a}}^3}}}{3}.\)
D. \(\frac{{{{\rm{a}}^3}\sqrt 2 }}{{12}}.\)
Cho khối lập phương \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) cạnh a. Thể tích của khối tứ diện \({\rm{AC}}{{\rm{B}}^\prime }{{\rm{D}}^\prime }\) là
A. \({{\rm{a}}^3}.\)
B. \(\frac{{{{\rm{a}}^3}}}{4}.\)
C. \(\frac{{{{\rm{a}}^3}}}{3}.\)
D. \(\frac{{{{\rm{a}}^3}\sqrt 2 }}{{12}}.\)
Cho khối hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có thể tích V. Thể tích của khối tứ diện \({\rm{A}}{{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{D}}^\prime }\) là
A. \(\frac{1}{3}\;{\rm{V}}.\)
B. \(\frac{1}{6}\;{\rm{V}}.\)
C. \(\frac{1}{5}\;{\rm{V}}.\)
D. \(\frac{1}{4}\;{\rm{V}}.\)
Tỉ số của thể tích khối chóp có đỉnh thuộc mặt đáy và khối hộp như hình vẽ bên là
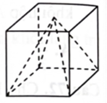
A. \(\frac{1}{3}.\)
B. \(\frac{1}{2}.\)
C. \(\frac{1}{6}.\)
D. \(\frac{1}{4}.\)
Khối chóp cụt tứ giác đều có độ dài các cạnh đáy là \({\rm{a}},{\rm{b}}\) và chiều cao h có thể tích bằng
A. \(\frac{1}{3}h\left( {{a^2} + ab + {b^2}} \right).\)
B. \(\frac{1}{3}\;{\rm{h}}\left( {{{\rm{a}}^2} + 2{\rm{ab}} + {{\rm{b}}^2}} \right).\)
C. \(\frac{1}{3}\;{\rm{h}}\left( {{{\rm{a}}^2} + 3{\rm{ab}} + {{\rm{b}}^2}} \right).\)
D. \(\frac{1}{3}h\left( {{a^2} - ab + {b^2}} \right).\)

