50 câu hỏi
Họ tất cả các nguyên hàm của hàm số \[f\left( x \right) = \cos 3x\] là
\[ - \frac{1}{3}\sin 3x + C.\]
\[\frac{1}{3}\sin 3x + C.\]
\[ - 3\sin 3x + C.\]
\[3\sin 3x + C.\]
Trong không gian Oxyz,cho mặt phẳng \[\left( P \right):x - 4y + 3z - 2 = 0.\] Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
\[\vec n = \left( {0; - 4;3} \right).\]
\[\vec n = \left( {1{\mkern 1mu} ;{\mkern 1mu} 4{\mkern 1mu} ;{\mkern 1mu} 3} \right).\]
\[\vec n = \left( { - 1;4; - 3} \right).\]
\[\vec n = \left( { - 4;3; - 2} \right).\]
Cho hàm số f(x) có bảng biến thiên như sau:
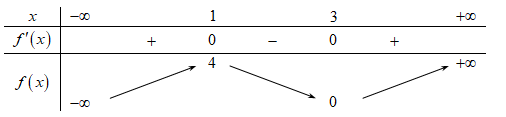
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
\[\left( { - \infty ;1} \right).\]
\[\left( {3; + \infty } \right).\]
\[\left( {0;4} \right).\]
\[\left( {1;3} \right).\]
Cho hàm số f(x) có bảng biến thiên như sau:
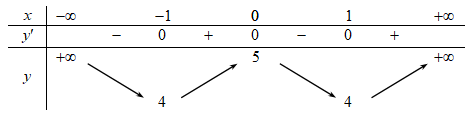
Giá trị cực đại của hàm số đã cho là
4.
0.
1.
5.
Tính đạo hàm của hàm số \[y = {\log _2}\sqrt {2x + 3} .\]
\[y' = \frac{2}{{2x + 3}}.\]
\[y' = \frac{1}{{2x + 3}}.\]
\[y' = \frac{2}{{\left( {2x + 3} \right)\ln 2}}.\]
\[y' = \frac{1}{{\left( {2x + 3} \right)\ln 2}}.\]
Giới hạn \[\lim \frac{1}{{2019n + 2020}}\] bằng
\[ + \infty .\]
0.
\[\frac{1}{{2019}}.\]
\[\frac{1}{{2020}}.\]
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ?
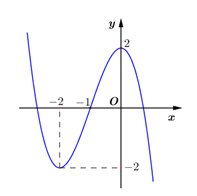
\[y = {x^3} - 3x + 2.\]
\[y = - {x^3} + 3x + 2.\]
\[y = {x^3} - 3{x^2} + 2.\]
\[y = - {x^3} - 3{x^2} + 2.\]
Cho hai số phức \[{z_1} = 1 + 2i,{\rm{ }}{z_2} = 2 - 3i.\] Số phức \[w = {z_1} + {z_2}\] có phần thực bằng
1.
\[ - 1.\]
\[ - i.\]
3.
Tích phân \[\int\limits_1^2 {\frac{{dx}}{{2x - 1}}} \] bằng
\[\frac{1}{2}\ln 3.\]
\[2\ln 3.\]
\[ - \frac{1}{2}\ln 3.\]
\[\ln 3.\]
Cho hàm số f(x) có bảng biến thiên như sau:
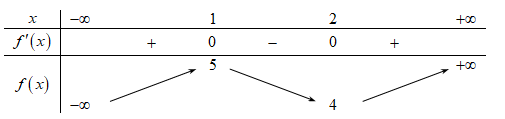
Phương trình \[2f\left( x \right) - 11 = 0\] có số nghiệm thực là
1.
2.
3.
0.
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng \[\left( P \right):2x - 3y + 4z - 1 = 0.\] Xét mặt phẳng \[\left( Q \right):\left( {2 - m} \right)x + \left( {2m - 1} \right)y + 12z - 2 = 0,\] với m là tham số thực. Tìm tất cả các giá trị thực của m để mặt phẳng (Q) song song với mặt phẳng (P).
\[m = - 6.\]
\[m = 4.\]
\[m = - 2\]
\[m = - 4.\]
Cho a và b là hai số thực dương tùy ý. Mệnh đề nào dưới đây là đúng?
\[{\log _2}\left( {\frac{{2{a^2}}}{b}} \right) = 1 + \frac{1}{2}{\log _2} + {\log _2}b.\]
\[{\log _2}\left( {\frac{{2{a^2}}}{b}} \right) = 1 + 2{\log _2} + {\log _2}b.\]
\[{\log _2}\left( {\frac{{2{a^2}}}{b}} \right) = 1 + \frac{1}{2}{\log _2} - {\log _2}b.\]
\[{\log _2}\left( {\frac{{2{a^2}}}{b}} \right) = 1 + 2{\log _2} - {\log _2}b.\]
Cho khối nón (N) có đường sinh bằng 5 và diện tích xung quanh bằng \[15\pi .\] Tính thể tích V của khối nón (N).
\[V = 12\pi .\]
\[V = 36\pi .\]
\[V = 15\pi .\]
\[V = 45\pi .\]
Có bao nhiêu số có 3 chữ số đôi một khác nhau và chia hết cho cả 2 và 5?
135.
22.
32.
72.
Cho phương trình phức \[{z^2} + bz + c = 0\] (\[b,{\rm{ }}c \in \mathbb{R}\]) có một nghiệm \[z = 1 + 2i.\] Tính \[S = b + c.\]
\[S = 7.\]
\[S = - 1.\]
\[S = 3.\]
\[S = - 3.\]
Cho hàm số f(x) liên tục trên \[\mathbb{R}.\] Gọi S là diện tích hình phẳng giới hạn bởi các đường \[y = f\left( x \right),{\rm{ }}y = 0,{\rm{ }}x = - 3\] và \[x = 0\] (như hình vẽ). Mệnh đề nào dưới đây là đúng?
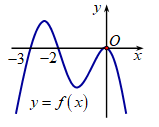
\[S = - \int\limits_{ - 3}^0 {f\left( x \right)dx} .\]
\[S = - \int\limits_{ - 3}^{ - 2} {f\left( x \right)dx} + \int\limits_{ - 2}^0 {f\left( x \right)dx} .\]
\[S = \int\limits_{ - 3}^0 {f\left( x \right)dx} .\]
\[S = \int\limits_{ - 3}^{ - 2} {f\left( x \right)dx} - \int\limits_{ - 2}^0 {f\left( x \right)dx} .\]
Tìm giá trị nhỏ nhất của hàm số \[y = {x^2} + \frac{{16}}{x}\] trên đoạn \[\left[ {1;4} \right].\]
\[\mathop {\min }\limits_{\left[ {1;4} \right]} {\mkern 1mu} y = 17.\]
\[\mathop {\min }\limits_{\left[ {1;4} \right]} {\mkern 1mu} y = 12.\]
\[\mathop {\min }\limits_{\left[ {1;4} \right]} {\mkern 1mu} y = 20.\]
\[\mathop {\min }\limits_{\left[ {1;4} \right]} {\mkern 1mu} y = 10.\]
Trong không gian Oxyz,cho hai vectơ \[\vec u = \left( {2; - 3;4} \right)\] và \[\vec v = \left( {m + 4; - 2{m^2} - 1;5m + 2} \right),\] với m là tham số thực. Tìm tất cả các giá trị thực của m để vectơ \[\vec u\] cùng phương với vectơ \[\vec v.\]
\[m = 2.\]
\[m = - \frac{5}{4}.\]
\[m = 3.\]
\[m = - 2.\]
Trên mặt phẳng tọa độ Oxy,cho tam giác ABCcó ba điểm \[A,{\rm{ }}B,{\rm{ }}C\] lần lượt biểu diễn các số phức \[{z_1} = 4 - 3i,{z_2} = - 2 + i,{\rm{ }}{z_3} = 1 - 4i.\] Trọng tâm của tam giác ABCbiểu diễn số phức nào dưới đây?
\[1 + 2i.\]
\[1 - 2i.\]
\[2 - i.\]
\[ - 2 + i.\]
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:
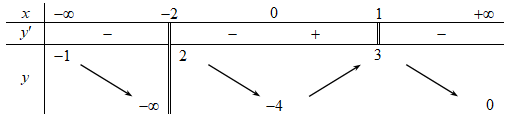
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
3.
2.
1.
4.
Cho \[{9^x} + {9^{ - x}} = 14.\] Tính giá trị của biểu thức \[P = \frac{{6 - 3\left( {{3^x} + {3^{ - x}}} \right)}}{{12 + {3^{x + 1}} + {3^{1 - x}}}}.\]
\[ - \frac{1}{6}.\]
\[\frac{1}{6}.\]
\[ - \frac{1}{4}.\]
\[\frac{1}{4}.\]
Cho lăng trụ tam giác đều \[ABC.A'B'C'\] có cạnh \[AB = 6,{\rm{ }}AA' = 8.\] Tính thể tích của khối trụ có hai đáy là hai đường tròn lần lượt nội tiếp tam giác ABCvà \[A'B'C'.\]
\[24\pi .\]
\[20\pi .\]
\[22\pi .\]
\[26\pi .\]
Có bao nhiêu giá trị nguyên của tham số m để hàm số \[y = {x^4} + 2\left( {{m^2} - 5m} \right){x^2} + 1\] có ba điểm cực trị?
4.
3.
2.
5.
Biết rằng \[\int\limits_0^{\frac{\pi }{3}} {{{\sin }^2}x\cos xdx} = \frac{{a + b\sqrt 3 }}{{16}},\] với \[a,{\rm{ }}b \in \mathbb{Z}.\] Tính \[S = a + 2b.\]
\[S = 4.\]
\[S = 2.\]
\[S = 8.\]
\[S = 6.\]
Cho hình hộp chữ nhật \[ABCD.A'B'C'D'\] có diện tích các mặt \[ABCD,{\rm{ }}ABB'A',{\rm{ }}ADD'A'\] lần lượt là 4, 9, 16. Thể tích của khối hộp \[ABCD.A'B'C'D'\] bằng
18.
24.
12.
30.
Biết phương trình \[{2^{x + 1}}{.5^x} = 15\] có nghiệm duy nhất dạng \[a\log 5 + b\log 3 + c\log 2\] với \[a,{\rm{ }}b,{\rm{ }}c \in \mathbb{Z}.\] Tính \[S = a + 2b + 3c.\]
\[S = 2.\]
\[S = 6.\]
\[S = 4.\]
\[S = 0.\]
Tập nghiệm của phương trình \[2{\log _2}\sqrt {x - 1} + {\log _2}\left( {x + 2} \right) = 2\] là
\[\left\{ {2;5} \right\}.\]
\[\left\{ {3;6} \right\}.\]
\[\left\{ 2 \right\}.\]
\[\left\{ 3 \right\}.\]
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Khoảng cách từ điểm A đến mặt phẳng \[\left( {SBD} \right)\] bằng \[\frac{{2a}}{3}.\] Tính thể tích của khối chóp \[S.ABC.\]
\[\frac{{{a^3}}}{2}.\]
\[\frac{{{a^3}}}{3}.\]
\[\frac{{{a^3}}}{6}.\]
\[\frac{{2{a^3}}}{3}.\]
Trong không gian Oxyz,cho đường thẳng \[d:\frac{{x - 1}}{1} = \frac{{y - 1}}{{ - 1}} = \frac{z}{1}\] và điểm \[A\left( {1; - 1; - 1} \right).\] Điểm \[H\left( {a;b;c} \right)\] là hình chiếu vuông góc của A trên d. Tính \[a + 2b + c.\]
1.
4.
2.
3.
Cho hàm số f(x) liên tục trên đoạn \[\left[ {1;e} \right]\] thỏa mãn \[\int\limits_1^e {\frac{{f\left( x \right)}}{x}dx} = 1\] và \[f\left( e \right) = 1.\] Tính tích phân \[I = \int\limits_1^e {f'\left( x \right).\ln xdx} .\]
\[I = 4\]
\[I = 3\]
\[I = 1\]
\[I = 0\]
Cho hình chóp S.ABCcó đáy ABClà tam giác vuông cân tại A và \[BC = 2a.\] Cạnh \[SA = \frac{a}{{\sqrt 3 }}\] và vuông góc với mặt phẳng đáy. Góc giữa hai mặt phẳng \[\left( {SBC} \right)\] và \[\left( {ABC} \right)\] bằng
\[90^\circ .\]
\[45^\circ .\]
\[30^\circ .\]
\[60^\circ .\]
Cho hàm số \[y = \ln \left( {{x^2} + 4} \right) + \left( {10 - {m^2}} \right)x\], với m là tham số thực. Có bao nhiêu giá trị nguyên của m để hàm số đồng biến trên khoảng \[\left( { - \infty ; + \infty } \right)\]?
5.
9.
7.
8.
Trong không gian Oxyz,cho hai đường thẳng
\[{d_1}:\left\{ {\begin{array}{*{20}{l}}{x = 3 + t}\\{y = 1 - 2t}\\{z = 4}\end{array}} \right.\left( {t \in \mathbb{R}} \right),{d_2}:\left\{ {\begin{array}{*{20}{l}}{x = 2 + t'}\\{y = 4}\\{z = 1 - 3t'}\end{array}} \right.\left( {t' \in \mathbb{R}} \right).\]Mặt phẳng \[\left( P \right):ax + by + cz - 2 = 0\] đi qua điểm \[A\left( {1; - 2;1} \right),\] đồng thời song song với đường thẳng \[{d_1}\] và \[{d_2}.\] Tính \[a + b + c.\]
1.
5.
11
7.
Cho số z thỏa mãn \[\left| {z + 8 - 3i} \right| = \left| {z - i} \right|\] và \[\left| {z + 8 - 7i} \right| = \left| {z + 4 - i} \right|\]. Môđun của z bằng
5
\[4\sqrt 2 .\]
\[2\sqrt 5 .\]
\[3\sqrt 5 .\]
Cho hàm số \[y = f\left( x \right)\] có đạo hàm liên tục trên \[\mathbb{R}\] và đồ thị hàm số \[y = f'\left( x \right)\] như hình vẽ. Bất phương trình \[f\left( x \right) \le {3^x} - 2x + m\] có nghiệm với mọi \[x \in \left( { - \infty ;1} \right]\] khi và chỉ khi
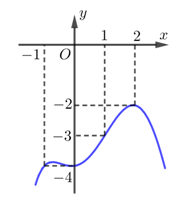
\[m \ge f\left( 1 \right) - 1\]
\[m >f\left( 1 \right) + 1\]
\[m \le f\left( 1 \right) - 1\]
\[m < f\left( 1 \right) - 1\]
</>
Trong không gian Oxyz,cho các điểm \[A\left( {1; - 2;3} \right),{\rm{ }}B\left( {5;0;0} \right),{\rm{ }}C\left( {0;2;1} \right)\] và \[D\left( {2;2;0} \right).\] Viết phương trình đường thẳng d đi qua A và vuông góc với mặt phẳng \[\left( {BCD} \right).\]
\[d:\frac{{x + 1}}{2} = \frac{{y - 2}}{3} = \frac{{z + 3}}{4}.\]
\[d:\frac{{x - 1}}{2} = \frac{{y + 2}}{3} = \frac{{z - 3}}{4}.\]
\[d:\frac{{x + 1}}{4} = \frac{{y - 2}}{3} = \frac{{z + 3}}{2}.\]
\[d:\frac{{x - 2}}{1} = \frac{{y - 3}}{{ - 2}} = \frac{{z - 4}}{3}.\]
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và \[\widehat {BAC} = 60^\circ .\] Cạnh \[SC = \frac{{a\sqrt 6 }}{2}\] và vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng \[SA\] và \[BD\] bằng
\[\frac{{a\sqrt {15} }}{{10}}.\]
\[\frac{{a\sqrt 6 }}{4}.\]
\[\frac{{a\sqrt 3 }}{3}.\]
\[\frac{{a\sqrt 3 }}{4}.\]
Cho (H) là hình phẳng giới hạn bởi parabol \[y = 2{x^2} - 1\] và nửa đường tròn có phương trình \[y = \sqrt {2 - {x^2}} \] (với \[ - \sqrt 2 \le x \le \sqrt 2 \]) (phần gạch chéo trong hình vẽ). Diện tích của (H) bằng
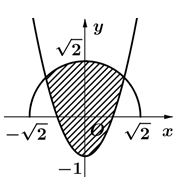
\[\frac{{3\pi + 2}}{6}.\]
\[\frac{{3\pi - 2}}{6}.\]
\[\frac{{3\pi + 10}}{6}.\]
\[\frac{{3\pi + 10}}{3}.\]
Chọn ngẫu nhiên một số tự nhiên A có 4 chữ số. Gọi N là số thỏa mãn \[{3^N} = A.\] Xác suất để N là số tự nhiên bằng
\[\frac{1}{{4500}}\]
\[\frac{1}{{3500}}\]
\[\frac{1}{{2500}}\]
\[\frac{1}{{3000}}\]
Biết rằng phương trình \[{m^2}{x^2}\left( {mx + 3} \right) = \left( {{x^2} + 2} \right)\sqrt {{x^2} + 1} - 4mx - 2\] (m là tham số thực) có nghiệm thuộc đoạn \[\left[ {1;2} \right]\] khi và chỉ khi \[m \in \left[ {a;b} \right]\] với \[a,{\rm{ }}b \in \mathbb{R}.\] Mệnh đề nào dưới đây là đúng?
\[a + b < 1.\]
\[a + b >2.\]
\[1 < a + b < \frac{3}{2}.\]
\[\frac{3}{2} < a + b < 2.\]
Cho hình trụ (T) có chiều cao bằng 2. Một mặt phẳng (P) cắt hình trụ (T) theo thiết diện là hình chữ nhật ABCD có các cạnh \[AB,{\rm{ }}CD\] lần lượt là các dây cung của hai đường tròn đáy. Biết cạnh \[AB = AD = 2\sqrt 5 ,\] tính thể tích của khối trụ đã cho.
\[20\pi .\]
\[16\pi .\]
\[22\pi .\]
\[18\pi .\]
Trong không gian Oxyz,cho mặt cầu \[\left( {{S_m}} \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - m} \right)^2} = \frac{{{m^2}}}{4}\] (\[m \ne 0\] và m là tham số thực) và hai điểm \[A\left( {2;3;5} \right)\], \[B\left( {1;2;4} \right)\]. Có bao nhiêu giá trị nguyên của m để trên \[\left( {{S_m}} \right)\] tồn tại điểm M sao cho \[M{A^2} - M{B^2} = 9\]?
11.
12.
13.
14.
Cho hàm số bậc bốn \[y = f\left( x \right)\] có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá trị thực của tham số m để phương trình \[f\left( {\left| {2020x + m} \right|} \right) = 6m + 12\] có đúng 4 nghiệm thực phân biệt. Tính tổng tất cả các phần tử của S.
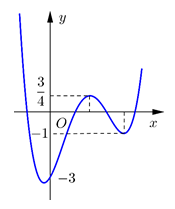
\[\frac{1}{2}.\]
\[ - \frac{1}{2}.\]
\[\frac{{97}}{{24}}.\]
\[ - \frac{{97}}{{24}}.\]
Cho hình lăng trụ \[ABC.A'B'C'\]. Gọi M, N, P lần lượt là các điểm thuộc các cạnh \[AA'\], \[BB'\], \[CC'\] sao cho \[AM = 2MA'\], \[NB' = 2NB\], \[PC = PC'\]. Gọi \[{V_1}\], \[{V_2}\] lần lượt là thể tích của hai khối đa diện \[ABCMNP\] và \[A'B'C'MNP\]. Tính tỉ số \[\frac{{{V_1}}}{{{V_2}}}\].
\[\frac{{{V_1}}}{{{V_2}}} = 2\]
\[\frac{{{V_1}}}{{{V_2}}} = \frac{1}{2}\]
\[\frac{{{V_1}}}{{{V_2}}} = 1\]
\[\frac{{{V_1}}}{{{V_2}}} = \frac{2}{3}\]
Cho hàm số f(x) có đạo hàm liên tục trên đoạn \[\left[ {0;1} \right]\], \[f\left( x \right)\] và \[f'\left( x \right)\] đều nhận giá trị dương trên đoạn \[\left[ {0;1} \right]\]. Biết rằng \[\int\limits_0^1 {\left[ {f'\left( x \right).{{\left[ {f\left( x \right)} \right]}^2} + 4} \right]} {\mkern 1mu} dx = 4\int\limits_0^1 {\sqrt {f'\left( x \right)} } .f\left( x \right)dx\] và \[f\left( 0 \right) = 3.\] Tích phân \[\int\limits_0^1 {{{\left[ {f\left( x \right)} \right]}^3}dx} \] bằng
33.
10.
21.
19.
Cho hàm \[y = f\left( x \right) = {x^4} - 6{x^3} + 12{x^2} - \left( {2m - 1} \right)x + 3m + 2\], với m là tham số thực. Có bao nhiêu giá trị nguyên của m để hàm số \[y = f\left( {\left| x \right|} \right)\] có đúng 7 điểm cực trị?
1.
2.
3.
4.
Tìm số nghiệm thực của phương trình \[{\left( {\left| x \right| - 1} \right)^2}.{e^{\left| x \right| - 1}} - \log 2 = 0.\]
2.
4.
0.
3.
Cho hai số thực \[a,{\rm{ }}b\] thỏa mãn \[a >b >\frac{4}{3}\] và \[16{\log _a}\left( {\frac{{{a^3}}}{{12b - 16}}} \right) + 3\log _{\frac{a}{b}}^2a\] đạt giá trị nhỏ nhất. Tính \[a + b.\]
\[\frac{7}{2}.\]
\[4.\]
\[\frac{{11}}{2}\]
\[6.\]
Trong không gian Oxyz,cho điểm \[A\left( {2; - 1; - 2} \right)\] và đường thẳng d có phương trình \[\frac{{x - 1}}{1} = \frac{{y - 1}}{{ - 1}} = \frac{{z - 1}}{1}\]. Mặt phẳng (P) đi qua A, song song với d và khoảng cách từ d tới (P) là lớn nhất. Mặt phẳng (P) vuông góc với mặt phẳng nào dưới đây?
\[x - y - 6 = 0.\]
\[x + 3y + 2z + 10 = 0.\]
\[x - 2y - 3z - 1 = 0.\]
\[3x + z + 2 = 0.\]
Cho hai số phức \[z,{\rm{ }}w\] thỏa mãn \[z + w = 3 + 4i\] và \[\left| {z - w} \right| = 9\]. Tìm giá trị lớn nhất của biểu thức \[T = \left| z \right| + \left| w \right|\].
4.
14.
\[\sqrt {176} .\]
\[\sqrt {106} .\]
