50 câu hỏi
Bạn muốn mua một áo sơ mi cỡ 40 hoặc 41. Áo cỡ 40 có 6 màu khác nhau, áo cỡ 41 có 4 màu khác nhau. Hỏi bạn có bao nhiêu cách chọn?
\(24\).
\(10\).
\(45\).
\(50\).
Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu tiên \({u_1} = 2\) và công bội \(q = - 3\). Số số hạng thứ 4 của cấp số nhân bằng
\(24\).
\(54\).
\( - 54\).
\( - 24\).
Nghiệm của phương trình \[{3^{1 - 2x}} = \frac{1}{3}\]là
\[x = - 1\].
\[x = 0\].
\[x = 2\].
\[x = 1\].
Thể tích của khối lăng trụ có đáy là hình vuông cạnh 2 và chiều cao 3 bằng
\[4\].
\[12\].
\[8\].
\[18\].
Tập xác định của hàm số \(y = {\log _3}\left( {4 - {x^2}} \right) + {2^{1 - 2x}}\) là
\(D = \left( { - 2;2} \right)\).
\(D = \left[ { - 2;2} \right]\).
\(D = \left( {2; + \infty } \right)\).
\(D = \left( {4; + \infty } \right)\).
Trong các khẳng định sau, khẳng định nào là sai?
\(\int {{x^\alpha }{\rm{d}}x = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\,\,\left( {\alpha \ne - 1} \right)} \).
\(\int {\sin x{\rm{d}}x = - \cos x + C} \).
\(\int {{a^x}{\rm{d}}x = \frac{{{a^x}}}{{\ln a}} + C\,\,\left( {0
\(\int {\frac{1}{x}{\rm{d}}x = \ln x + C\,\,\left( {x \ne 0} \right)} \).
Cho hình chóp tứ giác đều có đường cao và cạnh đáy đều bằng \(a\sqrt 3 \). Thể tích của khối chóp đã cho bằng:
\(3{a^3}\sqrt 3 \).
\(\frac{{{a^3}\sqrt 3 }}{3}\).
\({a^3}\sqrt 3 \).
\({a^3}\).
Cho hình nón \(\left( N \right)\) có bán kính đường tròn đáy bằng \(a\sqrt 3 \) và đường sinh tạo với đáy một góc \(30^\circ \). Thể tích khối nón \(\left( N \right)\) bằng:
\(\frac{1}{3}\pi {a^3}\).
\(\pi {a^3}\).
\(\frac{{\sqrt 3 }}{3}\pi {a^3}\).
\(3\pi {a^3}\).
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ. Hàm số \(y = f(x)\) đồng biến trên khoảng nào sau đây?
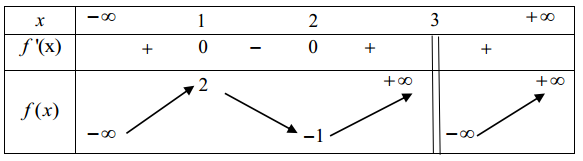
\(( - \infty \,,\,2)\).
\((1\,,\,3)\).
\((2\,,\, + \infty )\).
\((3\,,\, + \infty )\).
Cho \(a\) là một số thực dương khác 1, khi đó \({\log _a}\sqrt[3]{a}\)bằng:
\(3\).
\(\frac{1}{3}\).
\(\frac{1}{4}\).
4.
Cho hình trụ có chiều cao \[h = 4\] và bán kính đáy \[r = 5\]. Diện tích xung quanh của hình trụ đã cho bằng
\[{S_{xq}} = 40\pi \].
\[{S_{xq}} = 20\pi \].
\[{S_{xq}} = 80\pi \].
\[{S_{xq}} = 100\pi \].
Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\] và có bảng biến thiên như hình bên dưới.
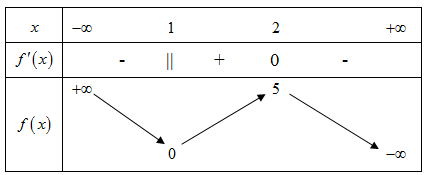
Điểm cực tiểu của đồ thị hàm số \[y = f\left( x \right)\] là
\[A\left( {1;0} \right)\].
\[B\left( {2;5} \right)\].
\[x = 1\].
\[x = 2\].
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?

\(y = \frac{{x + 2}}{{x - 1}}\).
\(y = \frac{{x - 2}}{{x - 1}}\).
\(y = \frac{{x - 2}}{{1 - x}}\).
\(y = \frac{{x + 2}}{{x + 1}}\).
Cho mặt cầu có diện tích là \(16\pi {a^2}\). Thể tích của khối cầu đã cho bằng
\(32\pi {a^3}\).
\(16\pi {a^3}\).
\(24\pi {a^3}\).
\(\frac{{32\pi {a^3}}}{3}\).
Tiệm cận ngang của đồ thị hàm số \(y = \frac{2}{{2 - x}}\) là
\(y = - 1\).
\(y = 0\).
\(y = - \frac{1}{2}\).
\(x = 2\).
Tập nghiệm của bất phương trình \({2^x} + {2^{x + 2}} \ge 5\) là\(\)\(\)
\(\left( {10\,;\, + \infty } \right)\).
\(\left( {0\,;\, + \infty } \right)\).
\(\left[ {0\,;\, + \infty } \right)\).
\(\left( { - \infty \,;\,10} \right)\).
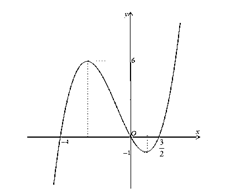
Cho hàm số đa thức bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(f\left( x \right)\, = \,0\) là
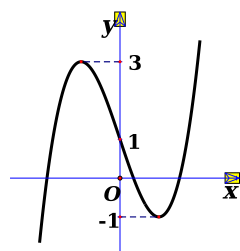
\(3\).
\(2\).
\(1\).
\(4\).
Cho \(\int\limits_2^5 {f\left( x \right){\rm{d}}x} = 10\) khi đó \(\int\limits_5^2 {\left[ {2 - 4f\left( x \right)} \right]{\rm{d}}x} \) bằng
\(42\).
\(38\).
\(34\).
\(32\).
Số phức liên hợp của số phức \(z = 2i - 1\) là:
\(\bar z = - 1 + 2i\).
\(\bar z = 2i + 1\).
\(\bar z = - 1 - 2i\).
\(\bar z = 1 - i\).
Cho hai số phức \({z_1} = 2 + 6i\) và \({z_2} = 1 - 5i\). Phần ảo của số phức \({z_1} + {z_2}\) bằng:
\(i\).
1.
3.
\( - i\).
Trong mặt phẳng \[Oxy\] điểm \(A,\,B\) lần lượt là điểm biểu diễn các số phức \(1 - 2i,\,3 - 2i\). Trung điểm \(D\) của đoạn \(AB\) là điểm biểu diễn của số phức \(z\) nào sau đây?
\(z = 4 - 4i\).
\(z = 2 - 2i\).
\(z = 2\).
\( - 1 + i\).
Trong không gian \[Oxyz\], hình chiếu vuông góc của điểm \(M\left( {9\,;\,8\,;\, - 1} \right)\) trên mặt phẳng \(Oyz\) có tọa độ là:
\(A\left( {0\,;\,8\,;\,0} \right)\).
\(A\left( {9\,;\,8\,;\,0} \right)\).
\(A\left( {9\,;\,0\,;\,0} \right)\).
\(A\left( {0\,;\,8\,;\, - 1} \right)\).
Trong không gian \(Oxyz\), cho điểm \(A\left( {1\,;\,2;\, - 1} \right)\) và mặt phẳng \(\left( P \right):\,\,x + y - 2z + 5 = 0\). Đường thẳng \(d\) đi qua \(A\) và vuông góc với \(\left( P \right)\) đi qua điểm nào sau đây?
\(M\left( { - 1\,;\,0;\,1} \right)\).
\(N\left( {0\,;\,1;\, - 3} \right)\).
\(P\left( {4\,;\,5;\,5} \right)\).
\(Q\left( {2\,;\,3;\, - 3} \right)\).
Cho hình lập phương \(ABCD.A'B'C'D'\) (như hình vẽ), tang của góc giữa đường thẳng \(B'D\) và mặt phẳng \(\left( {ABCD} \right)\) bằng
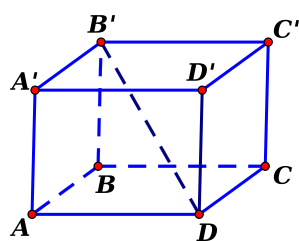
\(\frac{1}{{\sqrt 2 }}\).
\(\frac{1}{{\sqrt 3 }}\).
\(\sqrt 2 \).
\(\sqrt 3 \).
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\)và có đồ thị \(y = f'\left( x \right)\) như hình vẽ. Hàm số \(y = f\left( x \right)\)có bao nhiêu điểm cực tiểu trên khoảng \(\left( { - \frac{3}{2};\;5} \right)\)?
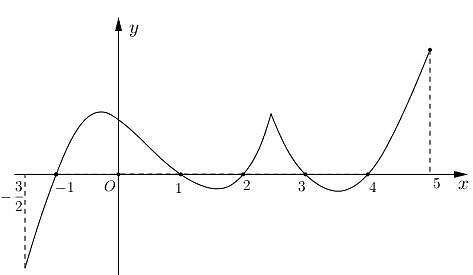
\(1\).
\(2\).
\(3\).
\(4\).
Gọi \(M,\;m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {x^3} - 3{x^2} + a\) trên đoạn \[{\rm{[ - 1;}}\;{\rm{3]}}\]. Nếu \(M = 2m\) thì khẳng định nào sau đây là đúng?
\(a \in \left( {1;\;4} \right)\).
\(a \in \left( {4;\;7} \right)\).
\(a \in \left( {7;\;10} \right)\).
\(a \in \left( {10;\;13} \right)\).
Gọi \({x_1}\),\({x_2}\)\(\left( {{x_1} < {x_2}} \right)\) là hai nghiệm của phương trình \({2^{{x^2} - 3x + 2}} = {3^{1 - x}}\). Khi đó \(S = {4^{{x_1}}} + {2^{{x_2} - 1}}\) bằng
\(\frac{{25}}{9}\).
\(\frac{{16}}{9}\).
\(\frac{9}{{16}}\).
\(2021\).
Số giao điểm của đồ thị hàm số \(y = {x^4} + 2{x^2} - 1\) và trục hoành bằng
\(1\).
\(3\).
\(0\).
\(2\).
Gọi \({z_1},{z_2}\) là hai nghiệm phức của phương trình \({z^2} + 2z + 2 = 0\) trong đó \({z_1}\) có phần ảo là số dương. Modul của số phức \(\omega = \left( {2{z_1} - {z_2}} \right){z_1}\) bằng
\(20\).
\(2\sqrt 5 \).
\(6\sqrt 5 \).
\(\sqrt 5 \)
Cho hình chóp \(S.ABC\) có \(SB \bot (ABC)\) và SB=4 ,AC = 2, góc ABC=60 độ. Tính diện tích mặt cầu ngoại tiếp hình chóp \(SABC\).
\(\frac{{48\pi }}{3}\).
\(\frac{{80\pi }}{3}\).
\(\frac{{64\pi }}{3}\).
\(\frac{{32\pi }}{3}\).
Cho hàm số \[y = f\left( x \right)\] liên tục trên \(\left[ {0; + \infty } \right)\) và thỏa mãn
\(f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 1}} - \frac{{x.f\left( {\sqrt {{x^2} + 4} } \right)}}{{\sqrt {{x^2} + 4} }}\).
Biết \(I = \int\limits_0^{2\sqrt 2 } {f\left( x \right){\rm{d}}x = - a + a} \ln b\,\left( {a;b \in \mathbb{N}} \right)\). Khi đó \(P = 2a - {b^3}\) bằng:
\( - 12\).
\( - 15\).
\( - 6\).
\( - 9\).
Cho hàm số \(y = f\left( x \right)\)là hàm bậc 4 có đồ thị \[\left( C \right)\] và \[d\] là tiếp tuyến của đồ thị \[\left( C \right)\] tại 2 điểm như hình vẽ.
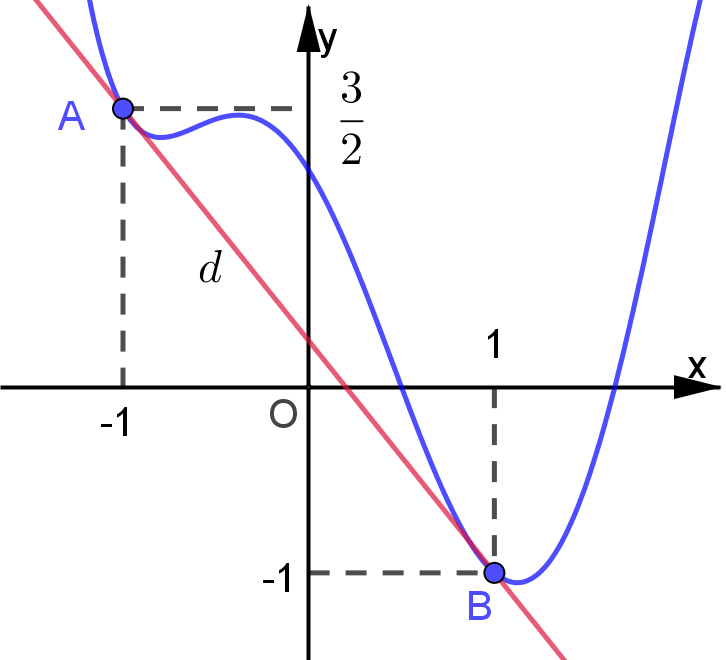
Biết diện tích hình phẳng giới hạn bởi đồ thị \[\left( C \right)\] và đường thẳng \[d\] là \(\frac{{11}}{3}\). Khi đó \(\int\limits_{ - 1}^1 {f\left( x \right){\rm{d}}x} \) bằng:
\(\frac{{19}}{6}\).
\(\frac{{25}}{6}\).
\(\frac{{23}}{6}\).
\(\frac{{13}}{3}\).
Cho số phức \(z = 2 + mi\,\,\left( {m \in \mathbb{R}} \right)\)thỏa \(\left( {2z - i} \right)\left( {2\overline z - 2} \right)\) là số thực. Giá trị \(\left| {2z - 3} \right|\) bằng
\(7\sqrt 2 \).
\(3\sqrt 2 \).
\(\sqrt 2 \).
\(5\sqrt 2 \).
Trong không gian \[Oxyz\], cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 6x + 4y - 12z + 41 = 0\). Từ điểm \(M\left( {2;\, - 1;\,3} \right)\) kẻ ba tiếp tuyến phân biệt \(MA,\,MB,\,MC\) đến mặt cầu (\(A,\,B,\,C\) là các tiếp điểm). Khi đó phương trình mặt phẳng \[\left( {ABC} \right)\] có dạng \[x + by + cz + d = 0\]. Giá trị \[b + c + d\] bằng
\[ - 12\].
\[ - 14\].
\[ - 13\].
\[11\].
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) sao cho phương trình \(\log _2^2x - \left( {m + 1} \right){\log _2}x + 2m - 3 = 0\,\)có đúng 2 nghiệm phân biệt thuộc khoảng \(\left( {2\,;\,16} \right)\) ?
\(2\).
\(1\).
\(3\).
\(4\).
Trong không gian biết tập hợp các điểm \(M\left( {x\,;\,y\,;\,z} \right)\) thỏa mãn \(\left| x \right| + \left| y \right| = 1\,,\,\left| z \right| \le 1\), làm thành các mặt bên của một khối lăng trụ. Thể tích của khối lăng trụ đó bằng:
\(1\).
\(2\).
\(3\).
\(4\).
Có bao nhiêu số tự nhiên lẻ có 6 chữ số đôi một khác nhau trong đó có 3 chữ số lẻ và 3 chữ số chẵn?
31680.
63360.
15840.
3600.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và \[AC = a.\] Biết tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với mặt phẳng đáy; góc giữa đường thẳng \(SD\) và mặt đáy bằng \(60^\circ .\) Khoảng cách giữa hai đường thẳng \(AD\) và \(SC\) bằng
\(\frac{{a\sqrt {609} }}{{19}}\).
\(\frac{{a\sqrt {609} }}{{29}}\).
\(\frac{{a\sqrt {600} }}{{29}}\).
\(\frac{{a\sqrt {906} }}{{29}}\).
Cho \[f\left( x \right)\] là hàm số đa thức có một phần đồ thị của hàm \[f'\left( x \right)\] như hình vẽ bên. Gọi \[F\left( x \right)\] là một nguyên hàm của hàm số \[f\left( x \right)\]. Tìm tất cả các giá trị của tham số \[m\] để hàm số \[y = F\left( x \right) + \left( {m - 1} \right)x + 2020\] đồng biến trên khoảng \[\left( { - 1\,;\,4} \right)\].
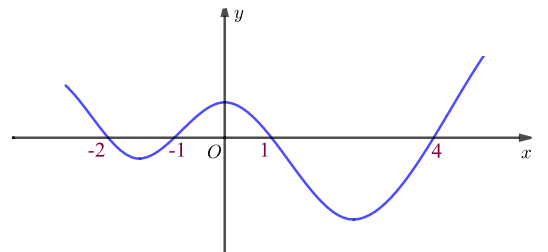
\[m >1 - f\left( { - 1} \right)\].
\[m \ge 1 - f\left( { - 1} \right)\].
\[m \ge 1 - f\left( 4 \right)\].
\[m >1 - f\left( 4 \right)\].
Ông A bị nhiễm một loại vi rút nên phải nhập viện và được điều trị ngay lập tức. Kể từ ngày bắt đầu nhập viện, sau mỗi ngày điều trị thì số lượng virut trong cơ thể ông A giảm đi \[10\% \] so với ngày trước đó. Hỏi sau ít nhất bao nhiêu ngày thì ông A sẽ được xuất viện biết ông được xuất viện khi lượng virut trong cơ thể của ông không vượt quá \[30\% \]?
11 ngày.
13 ngày.
12 ngày.
14 ngày.
Cho khối lăng trụ \[ABC.A'B'C'\] đáy là tam giác vuông cân tại \[A\]. Hình chiếu của \[A'\] lên mặt phẳng \[(ABC)\] là trung điểm \[H\] của đoạn \[AB\], khoảng cách giữa \[A'H\] và \[BC'\] bằng \[\frac{{4\sqrt 5 }}{5}\] và \[AA' = 3\]. Thể tích khối lăng trụ \[ABC.A'B'C'\] bằng
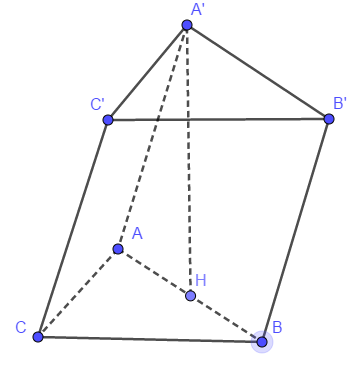
\[\frac{{8\sqrt 5 }}{3}\].
\[8\sqrt 5 \].
\[16\sqrt 5 \].
\[\frac{{16\sqrt 5 }}{3}\].
Cho hàm số \[f(x) = \frac{{ax + b}}{{x + c}}\], biết \[\mathop {\lim }\limits_{x \to 0} \frac{{f(x) + 3}}{x} = 5\] và tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \[x = 1\] có hệ số góc \[k = \frac{5}{4}\]. Khi đó giá trị của \[a + b + c\] bằng
\[0\].
\[1\].
\[2\].
\[ - 1\].
Cho hàm số bậc ba \(y = f(x)\) có đồ thị như hình vẽ bên. Có tất cả bao nhiêu giá trị nguyên dương của tham số \(m\) để phương trình \(\left| {f\left( {{x^3} - 3{x^2}} \right)} \right| - {\log _2}m = 0\) có 8 nghiệm phân biệt?
\(60.\)
\(63.\)
\(62.\)
\(61.\)
Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) thỏa mãn \(f(x) = \left\{ \begin{array}{l} - 3{x^2} + 6x + m{\rm{ khi }}x < 1\\\frac{{2x + 1}}{{x + 2}}{\rm{ khi }}x \ge 1\end{array} \right.\) (Với\(m\) là hằng số). Biết \(I = \int\limits_{\frac{1}{e}}^{{e^2}} {\frac{{f\left( {\ln x} \right)}}{x}{\rm{d}}x} + \int\limits_0^{\ln 2} {{e^x}f\left( {{e^x}} \right){\rm{d}}x} = a + b\ln 4 + c\ln 3\) với \(a,\,\,b,\,c\) là các số nguyên. Tổng \(a + 2b + 3c\) bằng
\(32.\)
\(4.\)
\(28.\)
\[16.\]
Cho hàm số \(y = \left| {\frac{1}{{x + 3}} - \frac{1}{x} + \frac{1}{{x - 2}} - \frac{1}{{x - 5}} - m} \right|\), với \(m\) là tham số. Có bao nhiêu giá trị nguyên của \(m\) để hàm số đã cho có giá trị nhỏ nhất trên \(\left( { - 3\,;5} \right)\backslash \left\{ {0\,;2} \right\}\) là một số dương?
\(3\).
\(1\).
Vô số.
\(2\).
Cho các số thực dương \(x,\,\,y\) thỏa mãn: \(3 + \left( {1 - {2^{\left| {x - 4} \right|}}} \right){.2^{\left| {y - 3} \right|}} = \left( {1 - {2^{ - \left| {y - 3} \right|}}} \right){.2^{2 - \left| {x - 4} \right|}}\) . Gọi \(M,\,\,m\) là giá trị lớn nhất và nhỏ nhất của biểu thức: \(P = {x^2} + {y^2} + 6x - 2y + 12\). Giá trị \(M.m\) bằng
\(1302\).
\(2697\).
\(4263\).
\(4165\).
Cho hình hộp chữ nhật \[ABCD.A'B'C'D'\]. Gọi \(N\) là trung điểm của \(B'C'\), \(P\) đối xứng với \(B\) qua \(B'\). Khi đó mặt phẳng \(\left( {PAC} \right)\) chia khối hộp thành hai phần. Tính tỉ số thể tích phần lớn và phần bé.
\(\frac{7}{3}\).
\(\frac{{17}}{7}\).
\(\frac{{25}}{7}\).
\(\frac{{25}}{{14}}\).
Có bao nhiêu cặp số nguyên \(a,\,\,b\) thỏa mãn đồng thời các điều kiện \({a^2} + {b^2} >1\) và \({a^2} + {b^2} - 3 \le {\log _{{a^2} + {b^2}}}\left( {\frac{{{b^2}\left( {{a^2} + {b^2} + 4} \right) + 4{a^2}}}{{{a^2} + 2{b^2}}}} \right)\)?
\(10\).
\(6\).
\(7\).
\(8\).
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right):{x^2} + {\left( {y + 2} \right)^2} + {\left( {z - 1} \right)^2} = 4\). Tâm \[I\]và bán kính \(R\)của mặt cầu \(\left( S \right)\) là
\(I\left( {0;\,2;\, - 1} \right),R = 2\) .
\(I\left( {0;\, - 2;\,1} \right),R = 2\).
\(I\left( {0;\,2;\, - 1} \right),R = 4\).
\(I\left( {0;\, - 2;\,1} \right),R = 4\).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):3x + y + 2z + 2020 = 0\). Véctơ nào dưới đây là một véctơ pháp tuyến của \(\left( P \right)\)?
\(\overrightarrow {{n_3}} = \left( {2;\,3;\,1} \right)\).
\(\overrightarrow {{n_1}} = \left( {3;\,2;\,1} \right)\).
\(\overrightarrow {{n_2}} = \left( {6;\,2;\,4} \right)\).
\(\overrightarrow {{n_4}} = \left( { - 2;\, - 3;\,1} \right)\).
