50 CÂU HỎI
Trong không gian Oxyz, cho mặt phẳng \[\left( P \right):x + 2y - 3z + 3 = 0.\] Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
A.\[\vec n = \left( {1; - 2;3} \right).\]
B.\[\vec n = \left( {1;2; - 3} \right).\]
C.\[\vec n = \left( { - 1;2; - 3} \right).\]
D.\[\vec n = \left( {1;2;3} \right).\]
Cho a và b là hai số thực dương tùy ý. Mệnh đề nào dưới đây là đúng?
A.\[\ln \left( {a{b^3}} \right) = \ln a + \frac{1}{3}\ln b.\]
B.\[\ln \left( {a{b^3}} \right) = \ln a - \frac{1}{3}\ln b.\]
C.\[\ln \left( {a{b^3}} \right) = \ln a + 3\ln b.\]
D.\[\ln \left( {a{b^3}} \right) = \ln a - 3\ln b.\]
Cho hàm số \[f\left( x \right)\] có bảng biến thiên như sau:
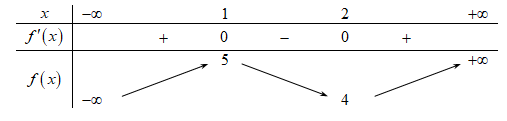
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.\[\left( {1;2} \right).\]
B.\[\left( { - \infty ;1} \right).\]
C.\[\left( {1; + \infty } \right).\]
D.\[\left( { - \infty ;5} \right).\]
Cho hàm số \[f\left( x \right)\] có đạo hàm trên đoạn \[\left[ {0;2} \right]\] và \[f\left( 0 \right) = - 1;{\rm{ }}f\left( 2 \right) = 2.\] Tích phân \[\int\limits_0^2 {f'\left( x \right)dx} \] bằng
A. −1.
B. 1.
C. −3.
D. 3.
Tính môđun của số phức z thỏa mãn \[z\left( {1 - i} \right) + 2i = 1.\]
A.\[\frac{{\sqrt 5 }}{2}.\]
B.\[\frac{{\sqrt {13} }}{2}.\]
C.\[\frac{{\sqrt {10} }}{2}.\]
D.\[\frac{{\sqrt {17} }}{2}.\]
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ?
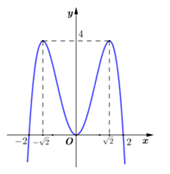
A.\[y = {x^4} - 3{x^2}.\]
B.\[y = - \frac{1}{4}{x^4} + 3{x^2}.\]
C.\[y = - {x^4} - 2{x^2}.\]
D.\[y = - {x^4} + 4{x^2}.\]
Tính đạo hàm của hàm số \[y = {\log _{\frac{3}{4}}}\left| x \right|.\]
A.\[y' = \frac{1}{{x\left( {\ln 3 - 2\ln 2} \right)}}.\]
B.\[y' = \frac{1}{{\left| x \right|\left( {\ln 3 - 2\ln 2} \right)}}.\]
C.\[y' = \frac{{\ln 3}}{{2x\ln 2}}.\]
D.\[y' = \frac{{\ln 3}}{{2\left| x \right|\ln 2}}.\]
Họ tất cả các nguyên hàm của hàm số \[f\left( x \right) = \sin 5x\] là
A.\[ - 5\cos 5x + C.\]
B.\[5\cos 5x + C.\]
C.\[ - \frac{1}{5}\cos 5x + C.\]
D.\[\frac{1}{5}\cos 5x + C.\]
Cho hàm số f(x) có bảng biến thiên như sau:
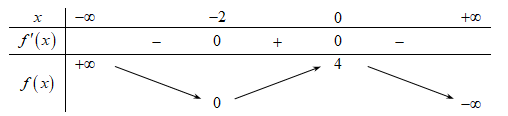
Giá trị cực đại của hàm số đã cho là
A. 4.
B. 0.
C. - 2.
D. 2.
Cho hàm số f(x) có bảng biến thiên như sau:
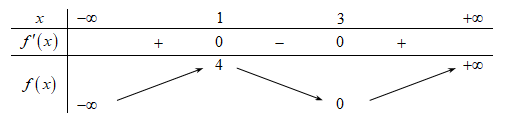
Phương trình \[3f\left( x \right) - 2 = 0\] có số nghiệm thực là
A. 1.
B. 2.
C. 3.
D. 0.
Trong không gian Oxyz, cho hai vectơ \[\vec u = \left( {3; - 4;5} \right)\] và \[\vec v = \left( {2m - n;1 - n;m + 1} \right),\] với \[m,{\rm{ }}n\] là các tham số thực. Biết rằng \[\vec u = \vec v,\] tính \[m + n.\]
A. −1.
B. 1.
C. −9.
D. 9.
Cho cấp số nhân \[\left( {{u_n}} \right)\] với \[{u_1} = 2,{\rm{ }}q = 4.\] Tổng của 5 số hạng đầu tiên bằng
A. \[\frac{{1023}}{2}.\]
B. 1364.
C. \[\frac{{341}}{2}.\]
D. 682.
Cho hàm số f(x) liên tục trên \[\mathbb{R}.\] Gọi S là diện tích hình phẳng giới hạn bởi các đường \[y = f\left( x \right),{\rm{ }}y = 0,{\rm{ }}x = 0\] và \[x = 4\] (như hình vẽ). Mệnh đề nào dưới đây là đúng?
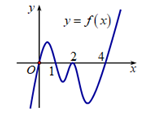
A.\[S = \int\limits_0^4 {f\left( x \right)dx} .\]
B.\[S = \int\limits_0^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} .\]
C.\[S = - \int\limits_0^4 {f\left( x \right)dx} .\]
D.\[S = - \int\limits_0^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} .\]
Cho khối nón (N) có bán kính đáy bằng 3 và diện tích xung quanh bằng 15π. Tính thể tích V của khối nón (N).
A.\[V = 36\pi .\]
B.\[V = 45\pi .\]
C.\[V = 15\pi .\]
D.\[V = 12\pi .\]
Kí hiệu \[{z_1},{\rm{ }}{z_2}\] là hai nghiệm phức của phương trình \[{z^2} + \left( {1 - 2i} \right)z - 1 - i = 0.\] Giá trị của \[\left| {{z_1}} \right| + \left| {{z_2}} \right|\] bằng
A.\[2 + \sqrt 2 .\]
B.\[1 + \sqrt 2 .\]
C.\[2 + \sqrt 5 .\]
D.\[1 + \sqrt 5 .\]
Phòng Nội Dung của Moon.vn cần chọn mua 1 tờ nhật báo mỗi ngày. Có 3 loại nhật báo. Hỏi có bao nhiêu cách chọn mua báo cho 6 ngày làm việc trong tuần?
A. 729.
B. 18.
C. 216.
D. 20.
Trong mặt phẳng Oxy, cho hai điểm A, BA, B như hình vẽ dưới đây. Trung điểm của đoạn thẳng \[AB\] biểu diễn số phức?
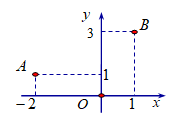
A.\[ - \frac{1}{2} + 2i.\]
B.\[2 - \frac{1}{2}i.\]
C.\[ - 1 + 2i.\]
D.\[ - 1 + 2i.\]
Cho \[a,{\rm{ }}b\] là các số thực dương thỏa mãn \[{a^2} + {b^2} = 8ab.\] Mệnh đề nào dưới đây là đúng?
A.\[\log \left( {a + b} \right) = \frac{1}{2}\left( {\log a + \log b} \right).\]
B.\[\log \left( {a + b} \right) = 1 + \log a + \log b.\]
C.\[\log \left( {a + b} \right) = \frac{1}{2}\left( {1 + \log a + \log b} \right).\]
D.\[\log \left( {a + b} \right) = \frac{1}{2} + \log a + \log b.\]
Tính thể tích của khối lập phương \[ABCD.A'B'C'D'\], biết \[AC' = 2a\sqrt 3 .\]
A.\[2{a^3}\sqrt 2 .\]
B.\[3{a^3}\sqrt 3 .\]
C.\[{a^3}.\]
D.\[8{a^3}.\]
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \[d:\left\{ \begin{array}{l}1x = 2 + 2t\\y = - 1 - 3t\\z = 1\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right).\] Xét đường thẳng \[\Delta :\frac{{x - 1}}{1} = \frac{{y - 3}}{m} = \frac{{z + 2}}{{ - 2}},\] với m là tham số thực khác 0. Tìm tất cả các giá trị thực của m để đường thẳng Δ vuông góc với đường thẳng d
A.\[m = 1.\]
B.\[m = 2.\]
C.\[m = \frac{2}{3}.\]
D.\[m = \frac{1}{3}.\]
Trong không gian, cho hình chữ nhật ABCD có \[AB = 6,{\rm{ }}AD = 4.\] Gọi \[M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q\] lần lượt là trung điểm của các cạnh \[AB,{\rm{ }}BC,{\rm{ }}CD,{\rm{ }}DA.\] Tính thể tích V của khối tròn xoay, nhận được khi quay tứ giác \[MNPQ\] xung quanh trục \[QN.\]
A.\[V = 2\pi .\]
B.\[V = 6\pi .\]
C.\[V = 8\pi .\]
D.\[V = 4\pi .\]
Tìm giá trị lớn nhất của hàm số \[y = \frac{{2x - 1}}{{x + 5}}\] trên đoạn \[\left[ { - 1;3} \right].\]
A.\[\frac{5}{3}.\]
B.\[ - \frac{3}{4}.\]
C.\[ - \frac{1}{5}.\]
D.\[\frac{5}{8}.\]
Giải phương trình \[{2^{10x - 1}} = {\left( {\frac{1}{{16}}} \right)^{x + 2}}.\]
A.\[x = - \frac{7}{{12}}.\]
B.\[x = - \frac{7}{{11}}.\]
C.\[x = - \frac{1}{2}.\]
D.\[x = - \frac{1}{3}.\]
Biết rằng \[\int\limits_2^3 {\frac{{x + 1}}{{x\left( {x - 2} \right) + 1}}dx} = a + b\ln 2,\] với \[a,{\rm{ }}b \in \mathbb{Z}.\] Tính \[S = a + 2b.\]
A.\[S = 1.\]
B.\[S = 4.\]
C.\[S = 3.\]
D.\[S = 5.\]
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Đường thẳng SB tạo với mặt phẳng (ABCD) một góc \[60^\circ .\] Thể tích của khối chóp S.ABCD bằng
A.\[\frac{{{a^3}\sqrt 3 }}{6}.\]
B.\[\frac{{{a^3}\sqrt 3 }}{3}.\]
C.\[\frac{{{a^3}}}{6}.\]
D.\[\frac{{{a^3}}}{3}.\]
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh \[SA = a\] và vuông góc với mặt phẳng đáy. Góc giữa hai mặt phẳng \[\left( {SBC} \right)\] và \[\left( {ABCD} \right)\] bằng
A.\[90^\circ .\]
B.\[45^\circ .\]
C.\[30^\circ .\]
D.\[60^\circ .\]
Biết hàm số \[y = f\left( x \right)\] có đạo hàm \[f'\left( x \right) = 3{x^2} + 2x - m + 1\] và \[f\left( 2 \right) = 1\]. Đồ thị của hàm số \[y = f\left( x \right)\] cắt trục tung tại điểm có tung độ bằng −5. Giá trị của \[f\left( 3 \right)\] là
A. 22.
B. \[ - 22.\]
C. 3.
D. \[ - 3.\]
Trong không gian Oxyz, cho đường thẳng \[d:\frac{{x - 1}}{1} = \frac{{y - 1}}{{ - 1}} = \frac{z}{1}\] và điểm \[A\left( {1; - 1; - 1} \right).\] Điểm \[H\left( {a;b;c} \right)\] là hình chiếu vuông góc của A trên d. Tính \[a + 2b + c.\]
A. 1.
B. 4.
C. 2.
D. 3.
Tìm số tiệm cận đứng của đồ thị hàm số \[y = \frac{{\sqrt {x + 1} + \sqrt {x + 4} - 3}}{{{x^3} - x}}.\]
A. 1.
B. 2.
C. 3.
D. 4.
Tập nghiệm của phương trình \[\frac{1}{2}{\log _3}{\left( {x + 2} \right)^2} + \frac{1}{3}{\log _3}{\left( {4x - 1} \right)^3} = 2\] là
A.\[\left\{ {7;\frac{5}{2}} \right\}.\]
B.\[\left\{ {1; - \frac{{11}}{4}} \right\}.\]
C.\[\left\{ 7 \right\}.\]
D.\[\left\{ 1 \right\}.\]
Cho hình nón có đỉnh S và đáy là đường tròn \[\left( {O;R} \right)\]. Trên đường tròn \[\left( {O;R} \right)\] lấy hai điểm \[A,{\rm{ }}B\] sao cho tam giác \[OAB\] vuông. Biết diện tích tam giác SAB bằng \[{R^2}\sqrt 2 .\] Tính thể tích V của khối nón đã cho.
A.\[V = \frac{{\pi {R^3}\sqrt {14} }}{2}\]
B.\[V = \frac{{\pi {R^3}\sqrt {14} }}{3}\]
C.\[V = \frac{{\pi {R^3}\sqrt {14} }}{6}\]
D.\[V = \frac{{\pi {R^3}\sqrt {14} }}{{12}}\]
Cho hàm số \[y = {x^3} - 3m{x^2} + 3\left( {2{m^2} - 10m + 9} \right)x\]. Có bao nhiêu giá trị nguyên của tham số m để hàm số đã cho có hai điểm cực trị?
A. 9.
B. 7.
C. 8.
D. 6.
Cho phương trình \[\log _2^2x - m{\log _2}x + 2m - 4 = 0\] (m là tham số thực) có hai nghiệm thực phân biệt \[{x_1},{\rm{ }}{x_2}\] thỏa mãn \[{x_1} + {x_2} = 20.\] Mệnh đề nào dưới đây là đúng?
A.\[4 < m \le 6.\]
B.\[m > 6.\]
C.\[2 < m \le 4.\]
D.\[0 < m \le 2.\]
Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số \[y = \frac{{x - 2}}{{x - m}}\] đồng biến trên khoảng \[\left( { - {\mkern 1mu} \infty ;{\mkern 1mu} - 1} \right)?\]
A. 3.
B. 4.
C. 2.
D. 5.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, \[AC = \frac{{a\sqrt 2 }}{2}.\] Cạnh bên SA vuông góc với mặt phẳng đáy và đường thẳng SB tạo với mặt phẳng \[\left( {ABCD} \right)\] một góc \[60^\circ .\] Khoảng cách giữa hai đường thẳng \[AD\] và \[SC\] bằng
A.\[\frac{{a\sqrt 3 }}{4}.\]
B.\[\frac{{a\sqrt 2 }}{2}.\]
C.\[\frac{{a\sqrt 3 }}{2}.\]
D.\[\frac{a}{2}.\]
Người ta muốn thiết kế một bể cá bằng kính không có nắp với thể tích \[72d{m^3}\] và chiều cao là \[3dm.\] Một vách ngăn (cùng bằng kính) ở giữa, chia bể cá thành hai ngăn, với các kích thước a, b (đơn vị dm) như hình vẽ. Tính a, b để bể cá tốn ít nguyên liệu nhất (tính cả tấm kính ở giữa), coi bề dày các tấm kính như nhau và không ảnh hưởng đến thể tích của bể.
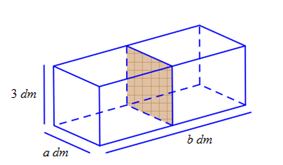
A.\[a = \sqrt {24} ,{\rm{ }}b = \sqrt {24} .\]
B.\[a = 3,{\rm{ }}b = 8.\]
C.\[a = 3\sqrt 2 ,{\rm{ }}b = 4\sqrt 2 .\]
D.\[a = 4,{\rm{ }}b = 6.\]
Trong không gian Oxyz, cho hai đường thẳng \[{d_1}:\frac{{x - 1}}{1} = \frac{y}{1} = \frac{{z - 1}}{{ - 1}}\] và \[{d_2}:\frac{{x + 4}}{1} = \frac{{y - 2}}{{ - 2}} = \frac{{z + 3}}{1}.\] Mặt phẳng \[\left( Q \right):ax + by + cz - 4 = 0\] chứa đường thẳng \[{d_1}\] và song song với đường thẳng \[{d_2}.\] Tính \[a + b + c.\]
A. 6.
B. 3.
C. −6.
D. −3.
Trong không gian Oxyz, cho hai đường thẳng
\[{d_1}:\frac{{x - 2}}{3} = \frac{{y + 3}}{1} = \frac{{z - 4}}{{ - 2}},{\rm{ }}{d_2}:\frac{{x - 4}}{3} = \frac{{y + 1}}{1} = \frac{z}{{ - 2}}.\] Phương trình nào sau đây là phương trình đường thẳng thuộc mặt phẳng chứa \[{d_1}\] và \[{d_2}\], đồng thời cách đều hai đường thẳng đó?
A.\[\frac{{x - 3}}{3} = \frac{{y + 2}}{1} = \frac{{z - 2}}{{ - 2}}.\]
B.\[\frac{{x + 3}}{3} = \frac{{y + 2}}{1} = \frac{{z + 2}}{{ - 2}}.\]
C.\[\frac{{x + 3}}{3} = \frac{{y - 2}}{1} = \frac{{z + 2}}{{ - 2}}.\]
D.\[\frac{{x - 3}}{3} = \frac{{y - 2}}{1} = \frac{{z - 2}}{{ - 2}}.\]
Có bao nhiêu số số phức z thỏa mãn \[\left| {z + 1} \right| = 2\sqrt 5 \] và \[{\left( {z - 1} \right)^2}\] là số thuần ảo?
A. 2.
B. 3.
C. 1.
D. 4.
Cho hàm số \[y = f\left( x \right)\] có đạo hàm liên tục trên \[\mathbb{R}\] và đồ thị hàm số \[y = f'\left( x \right)\] như hình vẽ. Bất phương trình \[f\left( x \right) > {x^3} + 4x + m\] nghiệm đúng với mọi \[x \in \left( {0;2} \right)\] khi và chỉ khi
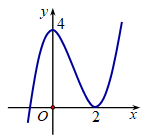
A.\[m < f\left( 0 \right).\]
B.\[m \le f\left( 0 \right).\]
C.\[m < f\left( 2 \right) - 16.\]
D.\[m \le f\left( 2 \right) - 16.\]
Cho A là tập các số tự nhiên có 7 chữ số. Lấy một số bất kỳ của tập A. Tính xác suất để lấy được số lẻ và chia hết cho 9.
A.\[\frac{{625}}{{1701}}\]
B.\[\frac{1}{9}\]
C.\[\frac{1}{{18}}\]
D.\[\frac{{1250}}{{1701}}\]
Xét các số thực \[a,{\rm{ }}b\] thỏa mãn điều kiện \[\frac{1}{3} < b < a < 1\]. Tìm giá trị nhỏ nhất của biểu thức \[P = {\log _a}\left( {\frac{{3b - 1}}{4}} \right) + 12\log _{\frac{b}{a}}^2a - 3.\]
A. 13.
B. \[\frac{1}{{\sqrt[3]{2}}}.\]
C. 9.
D. \[\sqrt[3]{2}.\]
Cho hàm số \[y = f\left( x \right)\] có đạo hàm tại \[x = 1\] và \[f'\left( 1 \right) \ne 0.\] Gọi \[{d_1}\], \[{d_2}\] lần lượt là hai tiếp tuyến của đồ thị hàm số \[y = f\left( x \right)\] và \[y = g\left( x \right) = x.f\left( {2x - 1} \right)\] tại điểm có hoành độ \[x = 1.\] Biết rằng hai đường thẳng \[{d_1}\], \[{d_2}\] vuông góc với nhau. Khẳng định nào sau đây đúng?
A.\[\sqrt 2 < \left| {f\left( 1 \right)} \right| < 2.\]
B.\[\left| {f\left( 1 \right)} \right| \le \sqrt 2 .\]
C.\[\left| {f\left( 1 \right)} \right| \ge 2\sqrt 2 .\]
D.\[2 \le \left| {f\left( 1 \right)} \right| < 2\sqrt 2 .\]
Cho hàm số f(x) liên tục trên \[\mathbb{R}\backslash \left\{ 0 \right\}\] thỏa mãn \[f\left( x \right) + 4f\left( {\frac{1}{x}} \right) = 8{x^2}.\] Tính tích phân \[I = \int\limits_{\frac{1}{2}}^2 {\frac{{f\left( x \right)}}{x}dx} .\]
A.\[I = \frac{3}{2}.\]
B.\[I = \frac{9}{2}.\]
C.\[I = 3.\]
D.\[I = 4.\]
Trong không gian Oxyz, cho mặt cầu \[\left( {{S_1}} \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 1.\] Xét mặt cầu \[\left( {{S_2}} \right):{\left( {x - 2} \right)^2} + {\left( {y - m} \right)^2} + {\left( {z - 1} \right)^2} = 16,\] với m là tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho \[\left( {{S_1}} \right)\] tiếp xúc với \[\left( {{S_2}} \right).\] Tính tổng tất cả các phần tử của S.
A. 6.
B. 10.
C. 4.
D. 8.
Cho hai số phức z, w thỏa mãn \[\left| {z + 2w} \right| = 3\], \[\left| {2z + 3w} \right| = 6\] và \[\left| {z + 4w} \right| = 7\]. Tính giá trị của biểu thức \[P = z.\bar w + \bar z.w\].
A.\[P = - 14i\]
B.\[P = - 28i\]
C.\[P = - 14\]
D.\[P = - 28\]
Cho hàm số f(x). Hàm số \[y = f'\left( x \right)\] có đồ thị như hình vẽ và \[f\left( 0 \right) + f\left( 1 \right) - 2f\left( 2 \right) = f\left( 4 \right) - f\left( 3 \right)\].
Mệnh đề nào dưới đây là đúng?
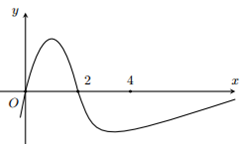
A.\[\mathop {\min }\limits_{\left[ {0;4} \right]} {\mkern 1mu} f\left( x \right) = f\left( 0 \right).\]
B.\[\mathop {\min }\limits_{\left[ {0;4} \right]} {\mkern 1mu} f\left( x \right) = f\left( 2 \right).\]
C.\[\mathop {\min }\limits_{\left[ {0;4} \right]} {\mkern 1mu} f\left( x \right) = f\left( 4 \right).\]
D.\[\mathop {\min }\limits_{\left[ {0;4} \right]} {\mkern 1mu} f\left( x \right) = f\left( 1 \right).\]
Cho hàm số f(x) có đồ thị như hình vẽ. Tìm số điểm cực trị của hàm số \[y = f\left[ {f\left( x \right)} \right]\].
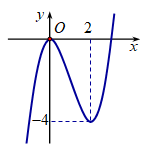
A. 5.
B. 3.
C. 4.
D. 6.
Gọi (H) là hình phẳng giới hạn bởi đồ thị (P) của hàm số \[y = 6x - {x^2}\] và trục hoành. Hai đường thẳng \[y = m,y = n\] chia hình (H) thành ba phần có diện tích bằng nhau. Tính \[P = {\left( {9 - m} \right)^3} + {\left( {9 - n} \right)^3}.\]
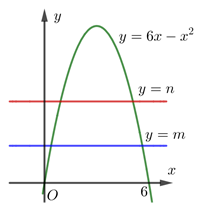
A.\[P = 405.\]
B.\[P = 409.\]
C.\[P = 407.\]
D.\[P = 403.\]
Trong không gian Oxyz, cho mặt cầu \[\left( S \right):{\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} + {z^2} = 4\] và hai điểm \[A\left( { - 1;2;0} \right),{\rm{ }}B\left( {2;5;0} \right).\] Điểm \[K\left( {a;b;c} \right)\] thuộc \[\left( S \right)\] sao cho \[KA + 2KB\] nhỏ nhất. Tính giá trị của \[a - b + c.\]
A.\[4 - \sqrt 3 .\]
B.\[ - \sqrt 3 .\]
C.\[4 + \sqrt 3 .\]
D.\[\sqrt 3 .\]


