Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (đề 15)
50 câu hỏi
Trong không gian Oxyz cho \(E\left( { - 1;0;2} \right)\) và \(F\left( {2;1; - 5} \right).\) Phương trình đường thẳng EF là
\[\frac{{x - 1}}{3} = \frac{y}{1} = \frac{{z + 2}}{{ - 7}}.\]
\(\frac{{x + 1}}{3} = \frac{y}{1} = \frac{{z - 2}}{{ - 7}}.\)
\(\frac{{x - 1}}{1} = \frac{y}{1} = \frac{{z + 2}}{{ - 3}}.\)
\(\frac{{x + 1}}{1} = \frac{y}{1} = \frac{{z - 2}}{3}.\)
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ như sau
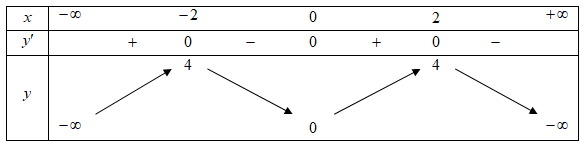
Hàm số đã cho nghịch biến trên khoảng nào dưới đây
\(\left( { - 4;0} \right).\)
\(\left( {2; + \infty } \right).\)
\(\left( { - 2;2} \right).\)
\(\left( {0;4} \right).\)
Tập tất cả các số thực x thỏa mãn \({\left( {\frac{2}{3}} \right)^{4x}} \le {\left( {\frac{3}{2}} \right)^{2 - x}}\) là:
\(\left[ { - \frac{2}{3}; + \infty } \right).\)
\(\left[ {\frac{2}{5}; + \infty } \right).\)
\(\left( { - \infty ;\frac{2}{5}} \right].\)
\(\left( { - \infty ;\frac{2}{3}} \right].\)
Cho cấp số nhân \(\left( {{u_n}} \right)\), với \({u_1} = - 9,{u_4} = \frac{1}{3}.\) Công bộ của cấp số nhân đã cho bằng
\(\frac{1}{3}.\)
\( - 3.\)
3.
\( - \frac{1}{3}.\)
Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây
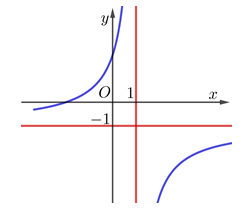
\(y = \frac{{ - x + 2}}{{x - 1}}.\)
\(y = \frac{{x - 1}}{{x + 1}}.\)
\(y = \frac{{ - x - 2}}{{x - 1}}.\)
\(y = \frac{{x - 2}}{{x - 1}}.\)
Trong không gian Oxyz cho \(\overrightarrow a \left( { - 3;4;0} \right)\) và \(\overrightarrow b \left( {5;0;12} \right)\). Côsin của góc giữa \(\overrightarrow a \) và \(\overrightarrow b \) bằng
\(\frac{3}{{13}}.\)
\(\frac{5}{6}.\)
\( - \frac{5}{6}.\)
\( - \frac{3}{{13}}.\)
Cho khối nón có bán kính đáy \(r = \sqrt 3 \) và chiều cao \(h = 4.\) Tính thể tích V của khối nón đã cho
\(V = 16\pi \sqrt 3 .\)
\(V = \frac{{16\pi \sqrt 3 }}{3}.\)
\(V = 12\pi .\)
\(V = 4\pi .\)
Có 3 kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và 4 kiểu dây (kim loại, da, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?
16.
7.
4.
12.
Trong không gian Oxyz, mặt phẳng \(\left( P \right)\) đi qua điểm \(M\left( {3; - 1;4} \right)\) đồng thời vuông góc với giá của vectơ \(\overrightarrow a \left( {1; - 1;2} \right)\) có phương trình là
\(3x - y + 4z - 12 = 0.\)
\(3x - y + 4z + 12 = 0.\)
\(x - y + 2z - 12 = 0.\)
\(x - y + 2z + 12 = 0.\)
Cho biểu thức \(P = \sqrt[3]{{x.\sqrt[4]{{{x^3}\sqrt x }}}},\) với \(x > 0.\) Mệnh đề nào dưới đây đúng?
\(P = {x^{\frac{1}{2}}}.\)
\(P = {x^{\frac{7}{{12}}}}.\)
\(P = {x^{\frac{5}{8}}}.\)
\(P = {x^{\frac{7}{{24}}}}.\)
Biết \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {a;b} \right]\) và \(2F\left( a \right) - 7 = 2F\left( b \right)\). Tính tích phân \(I = \int\limits_a^b {f\left( x \right)} dx.\)
\(I = - 2.\)
\(I = 2.\)
\(I = \frac{7}{2}.\)
\(I = \frac{{ - 7}}{2}.\)
Côsin góc tạo bởi cạnh bên và mặt đáy của hình chóp tứ giác đều có tất cả các cạnh bằng nhau là:
\(\frac{1}{2}.\)
\(\frac{1}{{\sqrt 3 }}.\)
\(\frac{{\sqrt 3 }}{2}.\)
\(\frac{1}{{\sqrt 2 }}.\)
Cho hai số phức \({z_1} = - 1 + 2i\) và \({z_2} = 4 - i.\) Điểm biểu diễn hình học của số phức \(z = {z_1} + 2{z_2}\) là
\(A\left( {3;1} \right).\)
\(B\left( { - 9;4} \right).\)
\(C\left( { - 9; - 4} \right).\)
\(D\left( {7;0} \right).\)
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\left( {a,b,c,d \in \mathbb{R}} \right)\) có đồ thị như hình vẽ
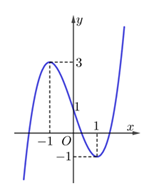
Giá trị cực đại của hàm số đã cho là
\({y_{C\~N }} = - 1.\)
\({y_{C\~N }} = 3.\)
\({y_{C\~N }} = 1.\)
\({y_{C\~N }} = 2.\)
Tất cả các nguyên hàm của hàm số \(f\left( x \right) = {3^{ - x}}\) là
\( - \frac{{{3^{ - x}}}}{{\ln 3}} + C.\)
\( - {3^{ - x}} + C.\)
\({3^{ - x}}\ln 3 + C.\)
\(\frac{{{3^{ - x}}}}{{\ln 3}} + C.\)
Cho hàm số \(y = a{x^4} + b{x^2} + c\left( {a,b,c \in \mathbb{R}} \right)\) có đồ thị như hình vẽ
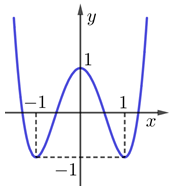
Số nghiệm của phương trình \(\left| {2f\left( x \right) + 1} \right| = 1\) là
3.
4.
5.
6.
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có tất cả các cạnh đều bằng a. Khoảng cách từ A đến mặt phẳng \(\left( {A'BC} \right)\) bằng
\(\frac{{a\sqrt 3 }}{4}.\)
\(\frac{{a\sqrt {21} }}{7}.\)
\(\frac{{a\sqrt 2 }}{2}.\)
\(\frac{{a\sqrt 6 }}{4}.\)
Biết hai số thực x, y thỏa mãn điều kiện \(\left( {x + 2yi} \right) + \left( {2 - xi} \right) = 1 + 5i\). Tính modun của số phức \(z = x + yi.\)
\(\left| z \right| = \sqrt 5 .\)
\(\left| z \right| = \sqrt {10} .\)
\(\left| z \right| = 3.\)
\(\left| z \right| = \sqrt 2 .\)
Đạo hàm của hàm số \(y = \ln \left| {{x^2} - 3x} \right|\) là
\(\frac{{2x - 3}}{{\left| {{x^2} - 3x} \right|}}.\)
\(\frac{{2x - 3}}{{{x^2} - 3x}}.\)
\(\frac{x}{{x - 3}}.\)
\(\frac{{2x - 3}}{{\left| {{x^2} - 3x} \right|\log x}}.\)
Giá trị lớn nhất của hàm số \(y = 2{x^3} + 3{x^2} - 12x + 2\) trên đoạn \(\left[ { - 1;2} \right]\) thuộc khoảng nào dưới đây?
\(\left( {3;8} \right).\)
\(\left( { - 7;8} \right).\)
\(\left( {2;14} \right).\)
\(\left( {12;20} \right).\)
Trong không gian với hệ tọa độ Oxyz, điều kiện cần và đủ để phương trình \({x^2} + {y^2} + {z^2} + 2x + 4y - 6z + {m^2} - 9m + 4 = 0\) là phương trình mặt cầu.
\( - 1 \le m \le 10.\)
\(m < - 1\) hoặc \(m > 10.\)
\(m > 0.\)
\( - 1 < m < 10.\)
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB = a,\) góc giữa đường thẳng \(A'C\) và mặt phẳng \(\left( {ABC} \right)\) bằng \(45^\circ .\) Thể tích của khối lăng trụ \(ABC.A'B'C'\) bằng
\(\frac{{{a^3}\sqrt 3 }}{4}.\)
\(\frac{{{a^3}\sqrt 3 }}{2}.\)
\(\frac{{{a^3}\sqrt 3 }}{{12}}.\)
\(\frac{{{a^3}\sqrt 3 }}{6}.\)
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x{\left( {{x^2} + 2x} \right)^3}\left( {{x^2} - \sqrt 2 } \right),\forall x \in \mathbb{R}.\) Số điểm cực trị của hàm số là
4.
1.
2.
3.
Cho a, b, c là các số thực dương khác 1. Biết \({\log _a}c = 2,{\log _b}c = 3.\) Tính \(P = {\log _c}\left( {ab} \right).\)
\(P = \frac{5}{6}.\)
\(P = 1.\)
\(P = \frac{2}{3}.\)
\(P = \frac{1}{2}.\)
Cho số phức z thỏa mãn \({\left( {1 - \sqrt 3 i} \right)^2}z = 3 - 4i.\) Môđun của z bằng
\(\frac{5}{4}.\)
\(\frac{5}{2}.\)
\(\frac{2}{5}.\)
\(\frac{4}{5}.\)
Phương trình \({\log _3}\left( {x + 2} \right) + \frac{1}{2}{\log _3}{\left( {x - 5} \right)^2} + {\log _{\frac{1}{3}}}8 = 0\) có tất cả bao nhiêu nghiệm thực?
1.
2.
3.
4.
Một mảnh giấy hình quạt như hình vẽ có bán kính \(AB = AC = 8\,\,cm.\) Người ta dán mép AB và AC lại với nhau để được một hình nón đỉnh A. Biết độ dài cung BC bằng \(8\pi \sqrt 3 \,\,cm,\) tính thể tích V của khối nón thu được (xem phần giấy dán không đáng kể)
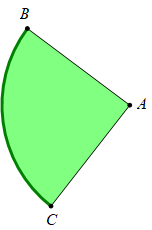
\(\frac{{256\pi }}{3}.\)
\(\frac{{64\pi }}{3}.\)
\(256\pi .\)
\(64\pi .\)
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ
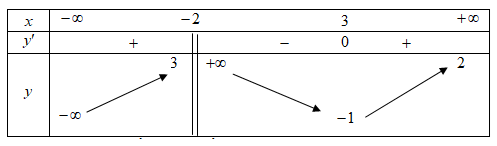
Số đường tiệm cận của đồ thị hàm số đã cho là
1.
2.
3.
4.
Cho hàm số \(y = a{x^4} + b{x^2} + c\left( {a,b,c \in \mathbb{R}} \right)\) có đồ thị như hình vẽ bên. Gọi S là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right),y = 0,x = - 2\) và \(x = 2\) (như hìnhh vẽ bên). Mệnh đề nào dưới đây là đúng
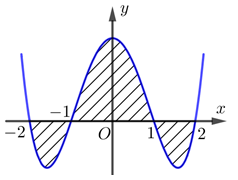
\(S = 2\int\limits_{ - 2}^{ - 1} {f\left( x \right)dx} + \int\limits_{ - 1}^1 {f\left( x \right)dx} .\)
\(S = 2\int\limits_{ - 2}^{ - 1} {f\left( x \right)dx} - \int\limits_{ - 1}^1 {f\left( x \right)dx} .\)
\(S = - 2\int\limits_{ - 2}^{ - 1} {f\left( x \right)dx} - \int\limits_{ - 1}^1 {f\left( x \right)dx} .\)
\(S = - 2\int\limits_{ - 2}^{ - 1} {f\left( x \right)d} x + \int\limits_{ - 1}^1 {f\left( x \right)dx} .\)
Trong không gian Oxyz, cho hai mặt phẳng \(\left( P \right):x - 3y + 2z - 1 = 0,\left( Q \right):x - z + 2 = 0.\)
\(x + y + z - 3 = 0.\)
\(x + y + z + 3 = 0.\)
\( - 2x + z + 6 = 0.\)
\( - 2x + z - 6 = 0.\)
Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = 2x + x\sin 3x\) là
\({x^2} + \frac{{\sin 3x}}{9} - \frac{{x\cos 3x}}{3} + C.\)
\({x^2} - \frac{{\sin 3x}}{9} + \frac{{x\cos 3x}}{3} + C.\)
\({x^2} - \frac{{\sin 3x}}{9} - \frac{{x\cos 3x}}{9} + C.\)
\({x^2} + \frac{{\sin 3x}}{3} - \frac{{x\cos 3x}}{3} + C.\)
Cho hàm số \(f\left( x \right)\) có \(f'\left( x \right) = \left( {x + 4} \right)\sqrt {x + 1} \) với mọi \(x > - 1\) và \(f\left( 0 \right) = 2.\) Tích phân \(\int_0^3 {f\left( x \right)dx} \) bằng
\(\frac{{1234}}{{35}}.\)
\(\frac{{1334}}{{35}}.\)
\(\frac{{267}}{7}.\)
\(\frac{{162}}{5}.\)
Trong không gian với hệ trục tọa độ Oxyz, viết phương trình đường vuông góc chung của hai đường chéo nhau \({d_1}\) và \({d_2}\) biết \({d_1}:\frac{{x - 2}}{1} = \frac{{y - 1}}{{ - 1}} = \frac{{z - 2}}{{ - 1}}\) và \({d_2}:\left\{ \begin{array}{l}x = t\\y = 3\\z = - 2 + t\end{array} \right.\).
\(\left\{ \begin{array}{l}x = 2 + t\\y = 1 + 2t\\z = 2 - t\end{array} \right..\)
\(\left\{ \begin{array}{l}x = - 3 - t\\y = - 3 - 2t\\z = - 1 + t\end{array} \right..\)
\(\left\{ \begin{array}{l}x = 2 + 3t\\y = 1 - 2t\\z = 2 - 5t\end{array} \right..\)
\(\left\{ \begin{array}{l}x = 3 + t\\y = 3\\z = 1 - t\end{array} \right..\)
Cho số phức z thỏa mãn \(4\left( {\overline z - i} \right) - \left( {3 - i} \right)z = - 1 - 29i.\) Mô đun của z bằng
\(\left| z \right| = 4.\)
\(\left| z \right| = \sqrt 5 .\)
\(\left| z \right| = 1.\)
\(\left| z \right| = 5.\)
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ
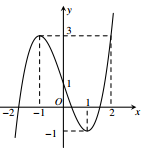
Hàm số \(y = f\left( {{x^2} - 2x + 1} \right) + 2018\) giảm trên khoảng
\(\left( { - \infty ;1} \right).\)
\(\left( {2; + \infty } \right).\)
\(\left( {0;1} \right).\)
\(\left( {1;2} \right).\)
Cho \(f\left( x \right)\) mà hàm số \(y = f'\left( x \right)\) có bảng biến thiên như hình bên. Tất cả các giá trị của tham số m để bất phương trình \(m + {x^2} < f\left( x \right) + \frac{1}{3}{x^3}\) nghiệm đúng với mọi \(x \in \left( {0;3} \right)\) là
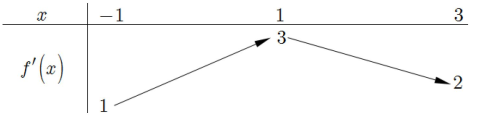
\(m < f\left( 0 \right).\)
\(m \le f\left( 0 \right).\)
\(m \le f\left( 3 \right).\)
\(m < f\left( 1 \right) - \frac{2}{3}.\)
Giải bóng chuyền VTV Cup gồm 12 đội bóng tham dự, trong đó có 9 đội nước ngoài và 3 đội của Việt Nam. Ban tổ chức cho bốc thăm ngẫu nhiên để chia thành 3 bảng A, B, C mỗi bảng 4 đội. Tính xác suất để 3 đội bóng của Việt Nam ở ba bảng khác nhau.
\(\frac{{16}}{{55}}.\)
\(\frac{{133}}{{165}}.\)
\(\frac{{36}}{{165}}.\)
\(\frac{{39}}{{65}}.\)
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a. Hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) cùng vuông góc với đáy. Biết rằng \(\left( {SBC} \right)\) tạo với đáy một góc \(45^\circ .\) Thể tích khối cầu ngoại tiếp khối chóp là:
\(\frac{{\pi {a^2}\sqrt 3 }}{2}.\)
\(\frac{{4\pi {a^3}\sqrt 3 }}{3}.\)
\(\frac{{\pi {a^3}\sqrt 3 }}{3}.\)
\(\frac{{\pi {a^3}\sqrt 3 }}{6}.\)
Cho các số thực dương a, b thỏa mãn \({\log _4}a = {\log _6}b = {\log _9}\left( {4a - 5b} \right) - 1.\) Đặt \(T = \frac{b}{a}.\) Khẳng định nào sau đây đúng?
\(1 < T < 2.\)
\(\frac{1}{2} < T < \frac{2}{3}.\)
\( - 2 < T < 0.\)
\(0 < T < \frac{1}{2}.\)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với \(AB = 2a,AD = 3a.\) Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi E là trung điểm của CD, tính khoảng cách giữa BE và SA
\(\frac{{3a\sqrt 2 }}{2}.\)
\(\frac{{6a\sqrt {13} }}{{13}}.\)
\(\frac{{3a}}{4}.\)
\(\frac{{12a}}{5}.\)
Nếu \(\int\limits_0^\pi {f\left( x \right)\sin xdx} = 20,\int\limits_0^\pi {x.f'\left( x \right)\sin xdx} = 5\) thì \(\int\limits_0^{{\pi ^2}} {f\left( {\sqrt x } \right)\cos \sqrt x dx} \) bằng
\( - 50.\)
\( - 30.\)
15.
25.
Cho phương trình \(\log _3^2\left( {3x} \right) - \left( {m + 2} \right){\log _3}x + m - 2 = 0\) (m là tham số thực). Tập hợp tất cả các giá trị của m để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn \(\left[ {\frac{1}{3};3} \right]\) là
\(\left( {0;2} \right).\)
\(\left[ {0;2} \right].\)
\(\left[ {0;2} \right).\)
\(\left( {2; + \infty } \right).\)
Trong không gian Oxyz, cho ba đường thẳng \(d:\frac{x}{1} = \frac{y}{1} = \frac{{z + 1}}{{ - 2}};{\Delta _1}:\frac{{x - 3}}{2} = \frac{y}{1} = \frac{{z - 1}}{1}\) và \({\Delta _2}:\frac{{x - 1}}{1} = \frac{{y - 2}}{2} = \frac{z}{1}.\) Đường thẳng \(\Delta \) vuông góc với d đồng thời cắt \({\Delta _1},{\Delta _2}\) tương ứng tại H, K sao cho độ dài HK nhỏ nhất. Biết rằng \(\Delta \) có một vectơ chỉ phương là \(\overrightarrow u = \left( {h;k;1} \right).\) Giá trị của \(h - k\) bằng
0.
4.
6.
\( - 2.\)
Cho hàm số \(f\left( x \right)\) có đồ thị hàm số \(y = f'\left( x \right)\) được cho như hình vẽ bên. Hàm số \(y = f\left( {\cos x} \right) + {x^2} - x\) đồng biến trên khoảng
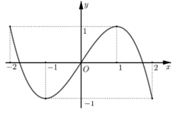
\(\left( {1;2} \right).\)
\(\left( { - 1;0} \right).\)
\(\left( {0;1} \right).\)
\(\left( { - 2; - 1} \right).\)
Giả sử \({z_1},{z_2}\) là hai trong các số phức z thỏa mãn \(\left( {z - 6} \right)\left( {8 + \overline {zi} } \right)\) là số thực. Biết rằng \(\left| {{z_1} - {z_2}} \right| = 4.\) Tập hợp điểm biểu diễn số phức \[w = {z_1} + {z_2}\] là một đường tròn có bán kính bằng
\(2\sqrt {21} .\)
\(\sqrt {21} .\)
6.
3.
Cho đường thẳng \(y = 4 - x\) và Parabol \(y = a\left( {4x - {x^2}} \right)\) (a là tham số thực dương). Gọi \({S_1}\) và \({S_2}\) lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi \({S_1} = {S_2}\) thì a thuộc khoảng nào sau đây
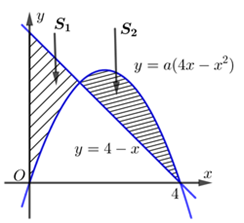
\(a \in \left( {0;\frac{1}{2}} \right).\)
\(a \in \left( {\frac{1}{2};\frac{4}{5}} \right).\)
\(a \in \left( {\frac{4}{5};1} \right).\)
\(a \in \left( {1;\frac{3}{2}} \right).\)
Cho khối lăng trụ \(ABC.A'B'C'\) có thể tích bằng 1. Gọi M, N lần lượt là trung điểm các đoạn thẳng \(AA',BB'.\) Mặt phẳng \(\left( {CMN} \right)\) cắt các đường thẳng \(C'A',C'B'\) lần lượt tại P, Q. Thể tích của khối đa diện lồi \(AA'P.BB'Q\) bằng
\(\frac{7}{3}.\)
\(\frac{4}{3}.\)
\(\frac{5}{3}.\)
4.
Trong không gian Oxyz cho \(\overrightarrow a = \left( {1; - 1;0} \right)\) và hai điểm \(A\left( { - 4;7;3} \right),B\left( {4;4;5} \right).\) Giả sử M, N là hai điểm thay đổi trong mặt phẳng \(\left( {Oxy} \right)\) sao cho \(\overrightarrow {MN} \) cùng hướng với \(\overrightarrow a \) và \(MN = 5\sqrt 2 .\) Giá trị lớn nhất của \(\left| {AM - BN} \right|\) bằng
\(\sqrt {17} .\)
\(\sqrt {77} .\)
\(7\sqrt 2 - 3.\)
\(\sqrt {82} - 5.\)
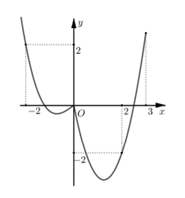
Cho hàm số \(f\left( x \right)\) có đồ thị hàm số \(y = f'\left( x \right)\) được cho như hình vẽ bên. Hàm số \(y = \left| {f\left( x \right) + \frac{1}{2}{x^2} - f\left( 0 \right)} \right|\) có nhiều nhất bao nhiêu điểm cực trị trong khoảng \(\left( { - 2;3} \right)\)?
6.
2.
5.
3.
Cho phương trình \(\log _2^2x - 2{\log _2}x - \sqrt {m + {{\log }_2}x} = m.\) Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 20;20} \right]\) để phương trình đã cho có nghiệm \(x \in \left( {0;1} \right).\)
21.
4.
19.
20.