25 CÂU HỎI
Cho hàm số y = 2\(\sqrt x - x\)với x > 0. Tính y'(1) có kết quả là
A. 3
B. 2
C. 0
D. 1
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA ^ (ABC). Chọn khẳng định đúng
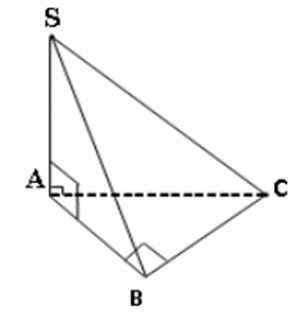
A. SA ^ SC
B. AB ^ AC
C. AB ^ SB
D. SA ^ BC
Mệnh đề nào sau đây đúng?
A. lim n = 0
B. lim \(\frac{{ - 1}}{n}\) = +¥
C. lim \(\frac{1}{{{n^3}}}\) = +¥
D. lim \({\left( {\frac{1}{4}} \right)^n}\)= 0
Tổng S = 1 + \(\frac{1}{2}\)+ \(\frac{1}{4}\)+ … + \(\frac{1}{{{2^n}}}\)+ … có giá trị là
A. S = \(\frac{3}{4}\)
B. S = \(\frac{3}{2}\)
C. S = 3
D. S = 2
Đạo hàm của hàm số y = 3sin2x + 2 là
A. y' = 6cos2x
B. y' = −6cos2x + 1
C. y' = 3cos2x – 2x
D. y' = 3cos2x + 2x
Mệnh đề nào sau đây sai?
A. \(\left( {\sqrt x } \right)' = \frac{1}{{\sqrt x }}(x > 0).\)
B. (c)' = 0 (c là hằng số).
C. (xn)' = n.xn – 1 (n Î ℕ, n > 1).
D. (x)' = 1.
bằng:
A. 2.
B. \(\frac{5}{2}\).
C. +¥.
D. −¥.
Hàm số nào sau đây gián đoạn tại x0 = 1?
A. y = \(\frac{{{x^2} + 2x - 3}}{{x - 1}}\)
B. y = x2 – 1.
C. y = (x – 1)2
D. y = \(\frac{{x - 6}}{{x + 1}}\)
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính \(\overrightarrow {AB} .\overrightarrow {EG} \) bằng
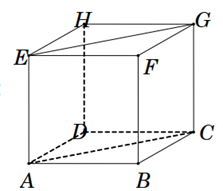
A. \({a^2}\frac{{\sqrt 2 }}{2}\)
B. a2
C. \({a^2}\sqrt 2 \)
D. \({a^2}\sqrt 3 \)
Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{3x + 1\,\,\,\,\,\,\,\,khi\,x \ne 1}\\{2x + 2a\,\,\,\,khi\,x = 1}\end{array}} \right.\). Giá trị của a để hàm số f(x) liên tục trên ℝ là
A. −2
B. 1
C. −1
D. 2
Cho hình chóp S.ABC có SA ^ (ABC).
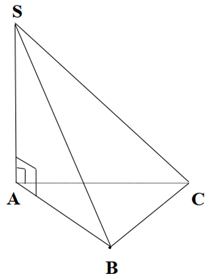
Góc giữa đường thẳng SC và mặt phẳng (ABC) là
A. SCB
B. SAC
C. SCA
D. CSA
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết rằng SA = SC, SB = SD. Khẳng định nào sau đây là đúng?
A. CD ^ AC
B. SO ^ (ABCD)
C. AB ^ (SAC)
D. CD ^ (SBD)
Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Đẳng thức đúng là
A. (uv)' = u'v + uv'
B. (uv)' = u'v'
C. (uv)' = u'v – uv'
D. (uv)' = uv
Cho hình hộp ABCD.A’B’C’D’. Khẳng định nào đúng?
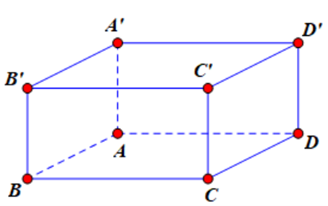
A. \(\overrightarrow {CB} + \overrightarrow {CD} + \overrightarrow {C'C} = \overrightarrow {CA'} \)
B. \(\overrightarrow {CB} + \overrightarrow {CD} + \overrightarrow {CC'} = \overrightarrow {CA'} \)
C. \(\overrightarrow {CB} + \overrightarrow {CD} + \overrightarrow {CC'} = \overrightarrow {CA} \)
D. \(\overrightarrow {CB} + \overrightarrow {CD} + \overrightarrow {CC'} = \overrightarrow {C'A'} \)
Cho hình lập phương ABCD.A’B’C’D’. Bộ ba vectơ nào sau đây đồng phẳng?
A. \(\overrightarrow {D'C'} ,\overrightarrow {D'D} ,\overrightarrow {AC} \)
B. \(\overrightarrow {B'C'} ,\overrightarrow {AD} ,\overrightarrow {A'B'} \)
C. \(\overrightarrow {CB} ,\overrightarrow {CD} ,\overrightarrow {CC'} \)
D. \(\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {AA'} \)
Trong các mệnh đề sau, mệnh đề nào sai?
A. \(\mathop {\lim }\limits_{x \to {0^ - }} \frac{1}{{{x^2}}} = - \infty \)
B. \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{{x^3}}} = + \infty \)
C. \(\mathop {\lim }\limits_{x \to {0^ - }} \frac{1}{{{x^4}}} = + \infty \)
D. \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{ - 1}}{{{x^4}}} = - \infty \)
Giới hạn \(\mathop {\lim }\limits_{x \to - 3} \frac{{{x^2} + 4x + 3}}{{x + 3}}\) có kết quả là:
A. −2
B. 1
C. 3
D. 5
Cho hai hàm số f(x), g(x) thỏa mãn \(\mathop {\lim }\limits_{x \to 1} f(x)\)= −6 và \(\mathop {\lim }\limits_{x \to 1} g(x)\)= 3. Giá trị của \(\mathop {\lim }\limits_{x \to 1} \left[ {f(x) - g(x)} \right]\) bằng:
A. −3
B. −9
C. 9
D. 3
Hàm số nào sau đây liên tục trên ℝ?
A. y = \(\frac{{x + 1}}{{{x^2} + x - 2}}\)
B. y = \(\frac{{x - 1}}{{x + 1}}\)
C. y = x3 + cotx
D. y = x3 + 3x2
Giới hạn \(\mathop {\lim }\limits_{x \to - 2} ({x^2} + x + 1)\) có kết quả là giá trị nào sau đây?
A. 5
B. 7
C. 1
D. 3
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính d(AB,(EFGH)).
A. 4a
B. 2a
C. a
D. 3a
Hàm số y = sinx có đạo hàm cấp hai là
A. y" = cosx
B. y" = sinx
C. y" = −cosx
D. y" = −sinx
Trong bốn giới hạn sau đây, giới hạn nào là −1?
A. un = \(\frac{{{n^2} + n}}{{ - 2n - {n^2}}}\)
B. un = \(\frac{{{n^3}}}{{{n^2} + 3}}\)
C. un = \(\frac{{2n + 3}}{{2 - 3n}}\)
D. un = \(\frac{{{n^2} - {n^3}}}{{2{n^3} + 1}}\)
Tính đạo hàm của hàm số y = \(\frac{{x + 1}}{{x - 2}}.\) Kết quả là
A. y' = \(\frac{3}{{{{(x - 2)}^2}}}\)
B. y' = \( - \frac{3}{{{{(x - 2)}^2}}}\)
C. y' = \( - \frac{1}{{{{(x - 2)}^2}}}\)
D. y' = \(\frac{1}{{{{(x - 2)}^2}}}\)
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \)và \(\overrightarrow {DH} \)?
A. 60°
B. 45°
C. 90°
D. 120°
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
