12 CÂU HỎI
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Nếu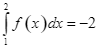 
thì 
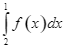bằng
A. −2.
B. 2.
C. 0.
D. 1.
Cho hàm số 
liên tục trên 
. Biết hàm số 
là một nguyên hàm của trên và 
. Tích phân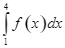 
bằng
A. −1.
B. 1.
C. 3.
D. 5.
Cho hàm số 
liên tục, không âm trên đoạn 
. Gọi 
là hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng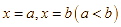 
. Thể tích của khối tròn xoay tạo thành khi quay quanh trục hoành được tính theo công thức
A.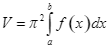 
.
B.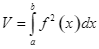 
.
C.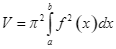 
.
D.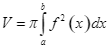 
.
Gọi 
là diện tích hình phẳng giới hạn bởi các đường 
. Mệnh đề nào sau đây đúng?
A.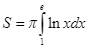 
.
B.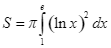 
.
C.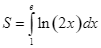 
.
D.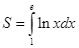 
.
Trong không gian 
, cho mặt phẳng 
. Vectơ nào dưới đây là một vectơ pháp tuyến của 
?
A. 
.
B. 
.
C. 
.
D. 
.
Trong không gian 
, vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng 
?
A. 
.
B. 
.
C. 
.
D. 
.
Trong không gian 
, cho đường thẳng 
đi qua điểm 
và nhận vectơ 
làm vectơ chỉ phương. Hệ phương trình nào sau đây là phương trình tham số của ?
A.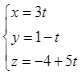 
.
B.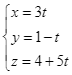 
.
C.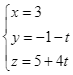 
.
D. 
.
Cho hai biến cố 
và 
. Xác suất của biến cố , tính trong điều kiện biết rằng biến cố đã xảy ra, được gọi là xác suất của với điều kiện kí hiệu là
A. 
.
B. 
.
C. 
.
D. 
.
Trong không gian 
, cho hai điểm 
và 
. Đường thẳng 
có phương trình là:
A.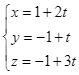 
.
B.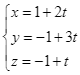 
.
C.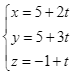 
.
D. 
.
Trong không gian với hệ tọa độ 
cho đường thẳng 
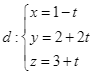và mặt phẳng 
. Tính số đo góc giữa đường thẳng 
và mặt phẳng 
.
A. 
.
B. 
.
C. 
.
D. 
.
Trong không gian 
, cho hai điểm 
. Phương trình của mặt cầu đường kính 
là:
A. 
.
B. 
.
C. 
.
D. 
Cho hai biến cố 
và 
với 
. Khi đó 
bằng
A. 
.
B. 
.
C. 
.
D. 
.
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải