Bộ 5 đề thi giữa kì 2 Toán 6 Kết nối tri thức cấu trúc mới có đáp án - Đề 5
21 câu hỏi
A. TRẮC NGHIỆM
Trong các cách viết sau đây, cách viết nào không phải là phân số?
\(\frac{{12}}{{ - 13}}.\)
\(\frac{{ - 18}}{{19}}.\)
\(\frac{0}{{ - 12}}.\)
\(\frac{0}{{ - 1,3}}.\)
Nếu \(\frac{x}{{ - 3}} = \frac{{ - 45}}{{15}}\) thì giá trị của \(x\) là
\(9.\)
\(15.\)
\(3.\)
\( - 9.\)
Rút gọn phân số \(\frac{{ - 32}}{{60}}\) đến tối giản ta được
\(\frac{{ - 16}}{{30}}.\)
\(\frac{{ - 8}}{{15}}.\)
\(\frac{8}{{15}}.\)
\(\frac{{16}}{{30}}.\)
Hỗn số \(5\frac{7}{9}\) được đọc là
Năm, bày phần chín.
Năm nhân bày phần chín.
Năm cộng bảy phần chín.
Năm và bảy phần chín.
Kết quả của phép tính \(\frac{1}{6} + \left( { - 1} \right) + \frac{5}{6}\) là
\(0.\)
\(1.\)
\(2.\)
\(\frac{2}{3}.\)
“Âm năm phẩy tám mươi ba” là cách đọc của số nào sau đây?
\( - 5,083.\)
\( - 5,83.\)
\( - 5,803.\)
\( - 5,38.\)
Số đối của số thập phân \( - 100,57\) là
\(\frac{{57}}{{100}}.\)
\(100,57.\)
\(\frac{{ - 100}}{{57}}.\)
\(57,100.\)
Số tự nhiên lớn nhất thỏa mãn \(x < 9,57\) là
\(9,56.\)
\(9,5.\)
\(8.\)
\(9.\)
Cho hình vẽ dưới đây.
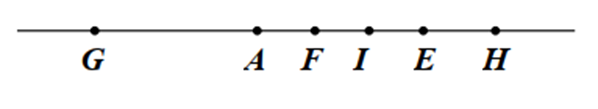
Điểm \(A\) và \(H\) nằm cùng phía đối với điểm nào?
Điểm \(E.\)
Điểm \(G.\)
Điểm \(F.\)
Điểm \(I.\)
Đọc tên tia trong hình vẽ sau:

Tia \(mA.\)
Tia \(Am.\)
Tia \(A.\)
Tia \(m.\)
Chọn phát biểu sai trong các phát biểu sau:
Nếu \(M\) là trung điểm của đoạn thẳng \(AB\) thì điểm \(M\) nằm giữa hai điểm \(A\) và \(B.\)
Nếu \(M\) là trung điểm của đoạn thẳng \(AB\) thì \(MA = MB = \frac{1}{2}AB.\)
Nếu \(MA = MB\) thì điểm \(M\) là trung điểm của đoạn \(AB\).
Nếu \(MA = MB\) và \(M\) nằm giữa hai điểm \(A\) và \(B\) thì \(M\) là trung điểm của đoạn thẳng \(AB\).
Cho \(I\) là trung điểm của đoạn thẳng \(AB\). Biết \(AB = 10{\rm{ cm}}{\rm{,}}\) số đo của đoạn thẳng \(IB\) là
\(5{\rm{ cm}}{\rm{.}}\)
\({\rm{10 cm}}{\rm{.}}\)
\({\rm{20 cm}}{\rm{.}}\)
\({\rm{2 cm}}{\rm{.}}\)
Hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Vào tháng 9, giá bán một chiếc máy tính là \(24{\rm{ }}000{\rm{ }}000\) đồng. Đến tháng 10, cửa hàng tăng giá lên \(20\% .\) Đến tháng 11, cửa hàng giảm \(20\% \) giá của tháng 10.
a) Tháng 10, cửa hàng đã tăng thêm \({\rm{4 8}}00{\rm{ }}000\) đồng so với giá tháng 9.
b) Tháng 10 cửa hàng bán máy tính với giá \(28{\rm{ 8}}00{\rm{ }}000\) đồng.
c) Tháng 11, cửa hàng đã giảm \({\rm{4 8}}00{\rm{ }}000\) đồng so với giá tháng 10.
d) Giá bán của chiếc máy tính đó vào tháng 11 đắt hơn tháng 9.
Hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Cho hai tia \(Ox\) và \(Oy\) đối nhau, trên tia \(Ox\) lấy hai điểm \(A\) và \(M\) sao cho \(OA = 5{\rm{ cm}}{\rm{, }}OM = 1{\rm{ cm}}\) trên tia \(Oy\) lấy điểm \(B\) sao cho \(OB = 3{\rm{ cm}}{\rm{.}}\)
a) Điểm \(M\) nằm giữa hai điểm \(O\) và \(A.\)
b) Điểm \(O\) nằm giữa hai điểm \(M\) và \(B\).
c) \(MA = 4{\rm{ cm}}{\rm{.}}\)
d) \(M\) là trung điểm của đoạn thẳng \(AB.\)
Hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Tìm giá trị của \(x,\) biết: \(5\frac{1}{4} + \frac{5}{4}x = - 3\).
(Kết quả ghi dưới dạng số thập phân)
Trả lời:
Hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Tìm giá trị của \(x,\) biết: \(53,2:\left( {x - 3,5} \right) + 45,8 = 99\).
(Kết quả ghi dưới dạng số thập phân)
Trả lời:
Hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Một mảnh vườn có diện tích \(374{\rm{ }}{{\rm{m}}^2}\) được chia làm hai mảnh. Tỉ số diện tích giữa mảnh nhỏ và mảnh lớn là \(37,5\% \). Hỏi diện tích của mảnh lớn là bao nhiêu mét vuông?
Trả lời:
Hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Trên tia \(Ot\) vẽ đoạn thẳng \(OB = 6{\rm{ cm}}{\rm{.}}\) Trên tia đối của tia \(Ot\) lấy điểm \(A,C\) sao cho \(3OA = OB\) và \(2OC = OB.\) Hỏi độ dài đoạn thẳng \(AC\) bằng bao nhiêu centimet?
Trả lời:
B. TỰ LUẬN
1. Một tấm vải bớt đi \(9{\rm{ m}}\) thì còn lại \(\frac{7}{{10}}\) tấm vải. Hỏi tấm vải đó dài bao nhiêu mét?
2. Một trường THCS có \(1{\rm{ }}200\) học sinh, trong đó số học sinh giỏi chiếm \(\frac{1}{3}\) học sinh toàn khối, số học sinh khá chiếm \(\frac{1}{4}\) số học sinh toàn trường, còn lại là số học sinh trung bình và yếu. Biết số học sinh yếu bằng \(\frac{1}{5}\) tổng số học sinh trung bình và yếu. Tìm số học sinh trung bình và học sinh yếu của trường đó.
Trên tia \[Ax\] lấy hai điểm \[B\] và \[C\] sao cho \[AB = 8{\rm{ cm}}{\rm{, }}AC = 6{\rm{ cm}}{\rm{.}}\]
a) Tính độ dài đoạn thẳng \[BC.\]
b) Trên tia đối của tia \[CB\] lấy điểm \[E\] sao cho \[C\] là trung điểm của \[BE.\] Chứng minh \[E\] là trung điểm của đoạn \[AB.\]
Cho \[A = 92 - \frac{1}{9} - \frac{2}{{10}} - \frac{3}{{11}} - ... - \frac{{92}}{{100}}\] và \[B = \frac{1}{{45}} + \frac{1}{{50}} + \frac{1}{{55}} + .... + \frac{1}{{500}}\]. Tính \[\frac{A}{B}.\]








