Bộ 5 đề thi giữa kì 2 Toán 11 Kết nối tri thức cấu trúc mới (Đề số 3)
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Với \(a\) là số thực dương tùy ý, \(\sqrt[{14}]{a}\) bằng
\({a^{\frac{1}{{14}}}}\).
\({a^{\sqrt {14} }}\).
\({a^{14}}\).
\(\sqrt {{a^{14}}} \).
Cho \(a,b\) là các số thực dương tùy ý. Khẳng định nào sau đây là đúng?
\(\ln \left( {a + b} \right) = \ln a.\ln b\).
\(\ln \left( {a + b} \right) = \ln a + \ln b\).
\(\ln \left( {ab} \right) = \ln a + \ln b\).
\(\ln \left( {ab} \right) = \ln a.\ln b\).
Nghiệm của phương trình \({3^x} = 1\) là
\(x = 2\).
\(x = - 1\).
\(x = 0\).
\(x = 1\).
Với hai số thực dương \(a,b\) tùy ý và \(\frac{{{{\log }_3}5.{{\log }_5}a}}{{1 + {{\log }_3}2}} - {\log _6}b = 2\). Khẳng định nào dưới đây là khẳng định đúng?
\(a = 36b\).
\(a = b{\log _6}3\).
\(2a + 3b = 0\).
\(a = b{\log _6}2\).
Có bao nhiêu số nguyên thuộc tập xác định của hàm số \(y = \log \left[ {\left( {6 - x} \right)\left( {x + 2} \right)} \right]\)?
\(7\).
\(8\).
Vô số.
\(9\).
Cho \({4^x} + {4^{ - x}} = 7\). Biểu thức \(P = \frac{{5 + {2^x} + {2^{ - x}}}}{{8 - {{4.2}^x} - {{4.2}^{ - x}}}}\) có giá trị bằng
\(P = \frac{3}{2}\).
\(P = - \frac{5}{2}\).
\(P = 2\).
\(P = - 2\).
Cho hình chóp \(S.ABCD\) có đáy là hình vuông. Gọi \(M,N\) lần lượt là trung điểm của \(SA\) và \(SC\).
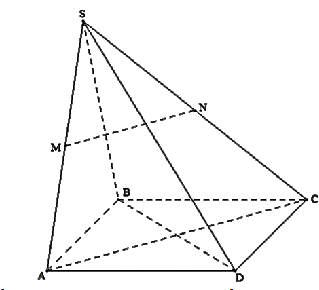
Chọn khẳng định đúng trong các khẳng định sau:
\(MN \bot BD\).
\(MN \bot SD\).
\(MN \bot SA\).
\(MN \bot SB\).
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(B\) và \(SA \bot \left( {ABC} \right)\).
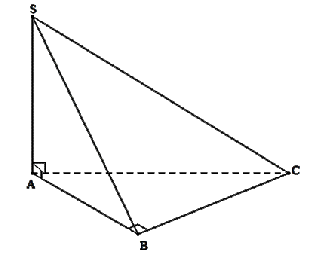
Hình chiếu của \(SC\) lên \(\left( {ABC} \right)\) là
\(SB\).
\(BC\).
\(AB\).
\(AC\).
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), tam giác \(ABC\) đều cạnh \(a\) và \(SA = a\) (tham khảo hình vẽ). Góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABC} \right)\) bằng
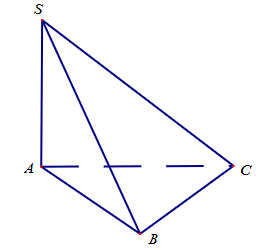
\(45^\circ \).
\(60^\circ \).
\(135^\circ \).
\(90^\circ \).
Trong các mệnh đề dưới đây, mệnh đề nào là đúng?
Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia.
Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này và vuông góc với giao tuyến của hai mặt phẳng sẽ vuông góc với mặt phẳng kia.
Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Cho hình lập phương \[ABCD.A'B'C'D'\] có cạnh bằng \(a\). Khoảng cách giữa hai đường thẳng \(AC\) và \(A'B'\) bằng bao nhiêu?
\(a\).
\(a\sqrt 2 \).
\(2a\).
\(\frac{1}{2}a\).
Một chụp đèn hình chóp cụt đều có chiều cao bằng 24 cm, đáy là lục giác đều, độ dài cạnh đáy lớn bằng 17,5 cm và độ dài cạnh đáy nhỏ bằng 10,5 cm. Thể tích phần không gian bên trong của chụp đèn này gần với kết quả nào sau đây?

37419.
12473.
12437.
37491.
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho bất phương trình \({\left( {3 - 2\sqrt 2 } \right)^{{x^2} - 4x}} > {\left( {3 + 2\sqrt 2 } \right)^{5 - 2x}}\).
a) Ta có : \(3 + 2\sqrt 2 = {\left( {3 - 2\sqrt 2 } \right)^{ - 1}}\).
b) Bất phương trình đã cho tương đương với bất phương trình : \({x^2} - 4x > 2x - 5\).
c) Số nghiệm nguyên của bất phương trình là 5.
d) Tổng các nghiệm nguyên của bất phương trình là 9.
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông cân tại \(B\), \(SA \bot \left( {ABC} \right),AB = BC = a\), \(SA = a\sqrt 3 \).
a) \(BC \bot \left( {SAB} \right)\).
b) Đường thẳng \(BC\) vuông góc với đường thẳng \(SB\).
c) Góc tạo bởi hai đường thẳng \(SB\) và \(AB\) bằng góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\).
d) Góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) bằng \(45^\circ \).
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 15 đến câu 18.
Cho \(a = {\log _2}5,b = {\log _3}5\). Biểu diễn \({\log _6}5\) theo \(a\) và \(b\) ta thu được kết quả dạng \(\frac{a}{{m + \frac{{n.a}}{b}}}\) với \(m;n\) là các số tự nhiên. Tính giá trị \(S = m - 2n\).
Biết \(x = a\) là nghiệm của phương trình \({\log _2}\left( {x - 1} \right) = 3\). Tìm a.
Cho tam giác \(ABC\) vuông cân tại \(A\) và \(BC = a\). Trên đường thẳng qua \(A\) vuông góc với \(\left( {ABC} \right)\) lấy điểm \(S\) sao cho \[SA = \frac{{a\sqrt 6 }}{2}\]. Số đo góc giữa đường thẳng \(SA\) và \(\left( {ABC} \right)\) bằng bao nhiêu độ ?
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \[2\sqrt 7 \], cạnh bên \[SA\] vuông góc với mặt phẳng đáy \[\left( {ABCD} \right)\]và \[SA = \sqrt {14} \]. Gọi \[M\] là trung điểm của cạnh \[BC\]. Tính khoảng cách giữa hai đường thẳng chéo nhau \[SB\] và \[DM\].
PHẦN II. TỰ LUẬN
Cho \(a > 0,b > 0,a \ne 1\). Rút gọn \(P = {\log _a}{a^3}{\log _a}b\).
Một người gửi tiết kiệm 100 triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn 6 tháng với lãi suất 8% một năm. Giả sử lãi suất không thay đổi. Hỏi sau bao nhiêu tháng người đó nhận được ít nhất 120 triệu đồng?
Một ngôi nhà có hai mái trước, sau có dạng là các hình chữ nhật \(ABCD,ABMN\) và \(AD = 4\;{\rm{m}}\), \(AN = 3\;{\rm{m}}\), \(DN = 5\;{\rm{m}}\)(hình vẽ minh hoạ). Tính góc nhị diện tạo bởi hai nửa mặt phẳng chứa hai mái nhà đó.