Bộ 5 đề thi giữa kì 2 Toán 11 Kết nối tri thức cấu trúc mới (Đề số 2)
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho \(a > 0,m,n \in \mathbb{R}\). Khẳng định nào sau đây đúng?
\({a^m} + {a^n} = {a^{m + n}}\).
\({a^m}.{a^n} = {a^{m - n}}\).
\({\left( {{a^m}} \right)^n} = {\left( {{a^n}} \right)^m}\).
\(\frac{{{a^m}}}{{{a^n}}} = {a^{n - m}}\).
Với các số thực dương \(a,b\) bất kì. Mệnh đề nào dưới đây đúng?
\(\log \left( {ab} \right) = \log a.\log b\).
\(\log \left( {ab} \right) = \log a + \log b\).
\(\log \frac{a}{b} = \frac{{\log a}}{{\log b}}\).
\(\log \frac{a}{b} = \log b - \log a\).
Trong các hàm số sau hàm số nào đồng biến trên tập xác định của nó?
\(y = {\left( {\frac{1}{2}} \right)^x}\).
\(y = 0,{5^x}\).
\(y = {x^2}\).
\(y = {\log _2}x\).
Cho hình chóp \(S.ABC\) có \(SA\, \bot \,\left( {ABC} \right)\), góc giữa \(SB\) và mặt phẳng \(\left( {ABC} \right)\) là.
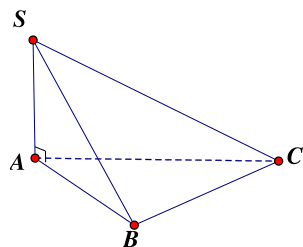
\(\widehat {SBA}\).
\(\widehat {SAB}\).
\(\widehat {SBC}\).
\(\widehat {SCB}\).
Cho hình chóp \(S.ABCD\) có \(SA\, \bot \,\left( {ABCD} \right)\). Khẳng định nào sau đây sai.
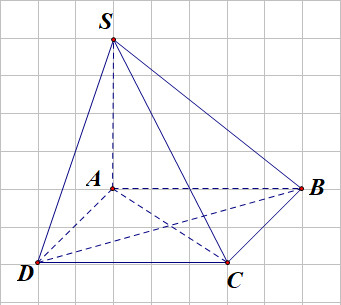
\(\left( {SBC} \right)\, \bot \,\left( {ABCD} \right)\).
\(\left( {SAB} \right)\, \bot \,\left( {ABCD} \right)\).
\(\left( {SAD} \right)\, \bot \,\left( {ABCD} \right)\).
\(\left( {SAC} \right)\, \bot \,\left( {ABCD} \right)\).
Thể tích của khối chóp có diện tích đáy bằng 6 và chiều cao bằng 3 là
\(V = 18\).
\(V = 6\).
\(12\).
\(24\).
Viết biểu thức \(P = \frac{{{a^2}{a^{\frac{5}{2}}}\sqrt[3]{{{a^4}}}}}{{\sqrt[6]{{{a^7}}}}}\), (\(a > 0\)) dưới dạng lũy thừa với số mũ hữu tỉ.
\(P = {a^5}\).
\(P = {a^{\frac{{14}}{3}}}\).
\(P = {a^4}\).
\(P = {a^{\frac{{13}}{3}}}\).
Mức cường độ âm \(L\) đo bằng decibel (viết tắt là dB, đọc là đề - xi – ben) của âm thanh có cường độ \(I\) (đo bằng oát trên mét vuông, kí hiệu là \({\rm{W/}}{{\rm{m}}^{\rm{2}}}\)) được định nghĩa \(L = 10\log \frac{I}{{{I_0}}}\), trong đó \({I_0} = {10^{ - 12}}{\rm{W/}}{{\rm{m}}^{\rm{2}}}\) là cường độ âm thanh nhỏ nhất mà tai người có thể phát hiện được (gọi là ngưỡng nghe). Xác định mức cường độ âm của âm thanh giao thông thành phố đông đúc có cường độ \(I = {10^{ - 3}}{\rm{W/}}{{\rm{m}}^{\rm{2}}}\).
\(90\).
\(130\).
\(110\).
\(150\).
Cho ba số thực dương \(a,b,c\) khác 1. Đồ thị các hàm số \(y = {a^x};y = {b^x};y = {c^x}\) được cho trong hình vẽ bên. Mệnh đề nào dưới đây đúng?
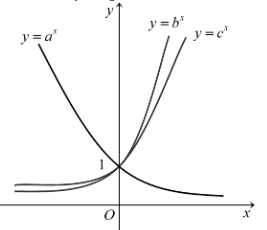
\(a < b < c\).
\(a < c < b\).
\(b < c < a\).
\(c < a < b\).
Cho hình chóp \(S.ABCD\) có đáy là hình vuông \(ABCD\) cạnh \(a\) và các cạnh bên bằng \(a\). Gọi \(M,N\) lần lượt là trung điểm \(AD\) và \(SD\). Số đo góc \(\left( {MN,SC} \right)\) bằng
\(60^\circ \).
\(45^\circ \).
\(30^\circ \).
\(90^\circ \).
Cho hình chóp \(S.ABC\), có đáy \(ABC\) là tam giác đều cạnh \(a\). Biết cạnh bên \(SA\) vuông góc với đáy và \(SA = \frac{{a\sqrt 3 }}{2}\) (tham khảo hình vẽ).
![Cho hình chóp S . A B C , có đáy A B C là tam giác đều cạnh a . Biết cạnh bên S A vuông góc với đáy và S A = a √ 3 2 (tham khảo hình vẽ). Số đo của góc phẳng nhị diện [ S , B C , A ] bằng (ảnh 1)](https://video.vietjack.com/upload2/images/1736660292/1736661042-image5.png)
Số đo của góc phẳng nhị diện \(\left[ {S,BC,A} \right]\) bằng
\(60^\circ \).
\(45^\circ \).
\(30^\circ \).
\(90^\circ \).
Cho khối lăng trụ đứng \[ABC.A'B'C'\] có đáy \[ABC\] là tam giác vuông cân tại \(B\), \[AB = a\]. Biết khoảng cách từ \(A\) đến mặt phẳng \[\left( {A'BC} \right)\] bằng \[\frac{{\sqrt 6 }}{3}a\], thể tích khối lăng trụ đã cho bằng
\(\frac{{\sqrt 2 }}{6}{a^3}\).
\(\frac{{\sqrt 2 }}{2}{a^3}\).
\(\sqrt 2 {a^3}\).
\(\frac{{\sqrt 2 }}{4}{a^3}\).
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho bất phương trình \({\log _{\frac{e}{3}}}2x < {\log _{\frac{e}{3}}}\left( {9 - x} \right)\).
a) Điều kiện xác định của bất phương trình \(0 < x < 9\).
b) Bất phương trình tương đương với bất phương trình \(2x < 9 - x\).
c) Tập nghiệm bất phương trình là \(\left( {3;9} \right)\).
d) Số nghiệm nguyên của bất phương trình là 3.
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật và \(SA\) vuông góc với mặt phẳng đáy. Gọi \(H,K\) theo thứ tự là hình chiếu của \(A\) trên các cạnh \(SB,SD\).
a) \(BC \bot SA\).
b) Tam giác \(SCD\) vuông.
c) \(SC \bot \left( {AHK} \right)\).
d) \(HK \bot SC\).
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 15 đến câu 18.
Với \(x > 0\), giả sử \(P = {x^{\frac{1}{3}}}.\sqrt[6]{x} = {x^{\frac{m}{n}}}\). Tính \(m + n\).
Cho \({\log _3}a = 2\) và \({\log _2}b = \frac{1}{2}\). Tính \(I = 2{\log _3}\left[ {{{\log }_3}\left( {3a} \right)} \right] + {\log _{\frac{1}{4}}}{b^2}\).
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(B\), \(SA\) vuông góc với đáy và \(SA = AB\). Góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {ABC} \right)\) bằng bao nhiêu độ?
Cho hình chóp đều \(S.ABCD\)có chiều cao \(\sqrt 3 ,\,\,AC = 2\sqrt 3 \). Tính khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( {SCD} \right)\).
PHẦN II. TỰ LUẬN
Với \(a,b\) là các số thực dương tùy ý thỏa mãn \(a \ne 1\) và \({\log _a}b = 2\). Tính giá trị của \({\log _{{a^2}}}\left( {a{b^2}} \right)\).
Dân số thế giới được tính theo công thức \(S = A.{e^{n.r}}\) trong đó \(A\) là dân số của năm lấy làm mốc tính, \(S\) là dân số sau \(n\) năm, \(r\) là tỉ lệ tăng dân số hằng năm. Cho biết năm 2005 Việt Nam có khoảng 80902400 người và tỉ lệ tăng dân số là 1,47% một năm. Như vậy nếu tỉ lệ tăng dân số hằng năm không đổi thì tối thiểu đến năm bao nhiêu dân của Việt Nam có khoảng 93713000 người?
Cho hình chóp tứ giác \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(2a\), \(SA\) vuông góc với mặt đáy \(\left( {ABCD} \right)\), góc giữa \(SB\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \(60^\circ \).
a) Chứng minh \(CD \bot \left( {SAD} \right)\).
b) Tính cosin góc giữa \(AC\) và \(\left( {SBD} \right)\).