12 CÂU HỎI
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho \(a > 0,m,n \in \mathbb{R}\). Khẳng định nào sau đây đúng?
A. \({a^m} + {a^n} = {a^{m + n}}\).
B. \({a^m}.{a^n} = {a^{m - n}}\).
C. \({\left( {{a^m}} \right)^n} = {\left( {{a^n}} \right)^m}\).
D. \(\frac{{{a^m}}}{{{a^n}}} = {a^{n - m}}\).
Với các số thực dương \(a,b\) bất kì. Mệnh đề nào dưới đây đúng?
A. \(\log \left( {ab} \right) = \log a.\log b\).
B. \(\log \left( {ab} \right) = \log a + \log b\).
C. \(\log \frac{a}{b} = \frac{{\log a}}{{\log b}}\).
D. \(\log \frac{a}{b} = \log b - \log a\).
Trong các hàm số sau hàm số nào đồng biến trên tập xác định của nó?
A. \(y = {\left( {\frac{1}{2}} \right)^x}\).
B. \(y = 0,{5^x}\).
C. \(y = {x^2}\).
D. \(y = {\log _2}x\).
Cho hình chóp \(S.ABC\) có \(SA\, \bot \,\left( {ABC} \right)\), góc giữa \(SB\) và mặt phẳng \(\left( {ABC} \right)\) là.
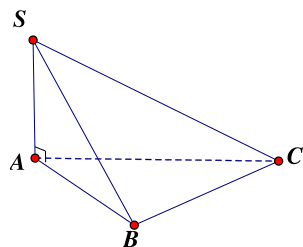
A. \(\widehat {SBA}\).
B. \(\widehat {SAB}\).
C. \(\widehat {SBC}\).
D. \(\widehat {SCB}\).
Cho hình chóp \(S.ABCD\) có \(SA\, \bot \,\left( {ABCD} \right)\). Khẳng định nào sau đây sai.
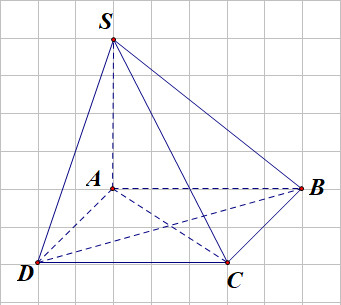
A. \(\left( {SBC} \right)\, \bot \,\left( {ABCD} \right)\).
B. \(\left( {SAB} \right)\, \bot \,\left( {ABCD} \right)\).
C. \(\left( {SAD} \right)\, \bot \,\left( {ABCD} \right)\).
D. \(\left( {SAC} \right)\, \bot \,\left( {ABCD} \right)\).
Thể tích của khối chóp có diện tích đáy bằng 6 và chiều cao bằng 3 là
A. \(V = 18\).
B. \(V = 6\).
C. \(12\).
D. \(24\).
Viết biểu thức \(P = \frac{{{a^2}{a^{\frac{5}{2}}}\sqrt[3]{{{a^4}}}}}{{\sqrt[6]{{{a^7}}}}}\), (\(a > 0\)) dưới dạng lũy thừa với số mũ hữu tỉ.
A. \(P = {a^5}\).
B. \(P = {a^{\frac{{14}}{3}}}\).
C. \(P = {a^4}\).
D. \(P = {a^{\frac{{13}}{3}}}\).
Mức cường độ âm \(L\) đo bằng decibel (viết tắt là dB, đọc là đề - xi – ben) của âm thanh có cường độ \(I\) (đo bằng oát trên mét vuông, kí hiệu là \({\rm{W/}}{{\rm{m}}^{\rm{2}}}\)) được định nghĩa \(L = 10\log \frac{I}{{{I_0}}}\), trong đó \({I_0} = {10^{ - 12}}{\rm{W/}}{{\rm{m}}^{\rm{2}}}\) là cường độ âm thanh nhỏ nhất mà tai người có thể phát hiện được (gọi là ngưỡng nghe). Xác định mức cường độ âm của âm thanh giao thông thành phố đông đúc có cường độ \(I = {10^{ - 3}}{\rm{W/}}{{\rm{m}}^{\rm{2}}}\).
A. \(90\).
B. \(130\).
C. \(110\).
D. \(150\).
Cho ba số thực dương \(a,b,c\) khác 1. Đồ thị các hàm số \(y = {a^x};y = {b^x};y = {c^x}\) được cho trong hình vẽ bên. Mệnh đề nào dưới đây đúng?
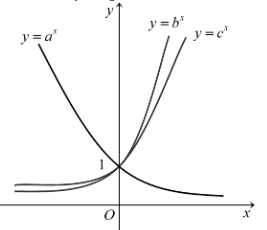
A. \(a < b < c\).
B. \(a < c < b\).
C. \(b < c < a\).
D. \(c < a < b\).
Cho hình chóp \(S.ABCD\) có đáy là hình vuông \(ABCD\) cạnh \(a\) và các cạnh bên bằng \(a\). Gọi \(M,N\) lần lượt là trung điểm \(AD\) và \(SD\). Số đo góc \(\left( {MN,SC} \right)\) bằng
A. \(60^\circ \).
B. \(45^\circ \).
C. \(30^\circ \).
D. \(90^\circ \).
Cho hình chóp \(S.ABC\), có đáy \(ABC\) là tam giác đều cạnh \(a\). Biết cạnh bên \(SA\) vuông góc với đáy và \(SA = \frac{{a\sqrt 3 }}{2}\) (tham khảo hình vẽ).
![Cho hình chóp S . A B C , có đáy A B C là tam giác đều cạnh a . Biết cạnh bên S A vuông góc với đáy và S A = a √ 3 2 (tham khảo hình vẽ). Số đo của góc phẳng nhị diện [ S , B C , A ] bằng (ảnh 1)](https://video.vietjack.com/upload2/images/1736660292/1736661042-image5.png)
Số đo của góc phẳng nhị diện \(\left[ {S,BC,A} \right]\) bằng
A. \(60^\circ \).
B. \(45^\circ \).
C. \(30^\circ \).
D. \(90^\circ \).
Cho khối lăng trụ đứng \[ABC.A'B'C'\] có đáy \[ABC\] là tam giác vuông cân tại \(B\), \[AB = a\]. Biết khoảng cách từ \(A\) đến mặt phẳng \[\left( {A'BC} \right)\] bằng \[\frac{{\sqrt 6 }}{3}a\], thể tích khối lăng trụ đã cho bằng
A. \(\frac{{\sqrt 2 }}{6}{a^3}\).
B. \(\frac{{\sqrt 2 }}{2}{a^3}\).
C. \(\sqrt 2 {a^3}\).
D. \(\frac{{\sqrt 2 }}{4}{a^3}\).
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải