12 CÂU HỎI
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho a là một số thực dương, biểu thức \({a^{\frac{2}{3}}}\sqrt a \)viết dưới dạng lũy thừa với số mũ hữu tỉ là
A. \({a^{\frac{5}{6}}}\).
B. \({a^{\frac{7}{6}}}\).
C. \({a^{\frac{{11}}{6}}}\).
D. \({a^{\frac{6}{5}}}\).
Cho \(a > 0,\,a \ne 1\), biểu thức \(D = {\log _{{a^3}}}a\) có giá trị bằng bao nhiêu?
A. \( - 3\).
B. \(3\).
C. \(\frac{1}{3}\).
D. \( - \frac{1}{3}\).
Nghiệm của phương trình \({\log _2}x = 3\) là
A. \(9\).
B. \(6\).
C. \(8\).
D. \(\frac{3}{2}\).
Mệnh đề nào đúng trong các mệnh đề sau?
A. Góc giữa hai đường thẳng bằng góc giữa hai vectơ chỉ phương của hai đường thẳng đó.
B. Góc giữa hai đường thẳng là góc nhọn.
C. Góc giữa hai đường thẳng \[a\] và \[b\] bằng góc giữa hai đường thẳng \[a\] và \[c\] khi \[b\] song song với \[c\] (hoặc \[b\] trùng với \[c\]).
D. Góc giữa hai đường thẳng \[a\] và \[b\] bằng góc giữa hai đường thẳng \[a\] và \[c\] thì \[b\] song song với \[c\].
Mệnh đề nào đúng trong các mệnh đề sau?
A. Góc giữa đường thẳng và mặt phẳng (đường thẳng không vuông góc với mặt phẳng) bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho.
B. Góc giữa đường thẳng \[a\] và mặt phẳng \[\left( P \right)\] bằng góc giữa đường thẳng \[b\] và mặt phẳng \[\left( P \right)\] khi \[a\] và \[b\] song song (hoặc \[a\] trùng với \[b\]).
C. Góc giữa đường thẳng \[a\] và mặt phẳng \[\left( P \right)\] bằng góc giữa đường thẳng \[a\] và mặt phẳng \[\left( Q \right)\] thì mặt phẳng \[\left( P \right)\] song song với mặt phẳng \[\left( Q \right)\].
D. Góc giữa đường thẳng \[a\] và mặt phẳng \[\left( P \right)\] bằng góc giữa đường thẳng \[b\] và mặt phẳng \[\left( P \right)\] thì \[a\] và \[b\] song song.
Mệnh đề nào sau đây là đúng?
A. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia.
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này và vuông góc với giao tuyến của hai mặt phẳng sẽ vuông góc với mặt phẳng kia.
Cường độ một trận động đất M (richter) được cho bởi công thức \(M = \log A - \log {A_0}\), với \(A\) là biên độ rung chấn tối đa và \({A_0}\) là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San Francisco có cường độ 8 độ Richter. Trong cùng năm đó, trận động đất khác Nam Mỹ có biên độ mạnh hơn gấp 4 lần. Cường độ của trận động đất ở Nam Mỹ gần với số nào sau đây nhất là
A. \(8,9\).
B. \(7,9\).
C. \(8,6\).
D. \(8,4\).
Cho đồ thị hai hàm số \(y = {a^x}\) và \(y = {\log _b}x\) như hình vẽ
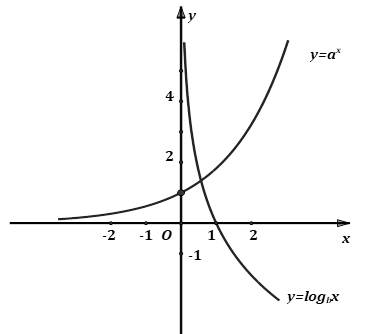
A. \(a > 1;b > 1\).
B. \(a > 1;0 < b < 1\)
C. 0
D.\(0 < a < 1;b > 1\).
Nghiệm của phương trình \({\left( {\frac{1}{{25}}} \right)^{x + 1}} = {125^{2x}}\) là
A. \(x = 1\).
B.\(x = 4\).
C. \(x = - \frac{1}{4}\).
D.\(x = - \frac{1}{8}\).
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B,\) cạnh bên \(SA\) vuông góc với đáy. Gọi \(H\) là chân đường cao kẻ từ \(A\) của tam giác \(SAB\). Khẳng định nào dưới đây là sai?
A. \(SA \bot BC\).
B. \(AH \bot BC\).
C. \(AH \bot AC\).
D. \(AH \bot SC\).
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\) và đáy \(ABC\) là tam giác đều. Khẳng định nào sau đây sai?
A. \(\left( {SAB} \right) \bot \left( {ABC} \right)\).
B. Gọi \(H\) là trung điểm của cạnh \(BC\). Khi đó \(\widehat {AHS}\) là góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right).\)
C. Góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SAC} \right)\) là \(\widehat {ACB}\).
D. \(\left( {SAC} \right) \bot \left( {ABC} \right)\).
Cho khối lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông cân tại \(A\), \(AB = 2a\). Góc giữa đường thẳng \(BC'\) và mặt phẳng \(\left( {ACC'A'} \right)\) bằng \(30^\circ \). Thể tích của khối lăng trụ đã cho bằng
A. \(3{a^3}\).
B. \({a^3}\).
C. \(12\sqrt 2 {a^3}\).
D. \(4\sqrt 2 {a^3}\).
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải