11 CÂU HỎI
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho mẫu số liệu về chiều cao (cm) của các học sinh nữ trong khối 11 của một trường như sau:
Số học sinh nữ cao từ 150 cm đến 155 cm là
A. \(20\).
B. \(65\).
C. \(34\).
D. \(45\).
Gieo hai con xúc xắc cân đối và đồng chất. Gọi \(A\) là biến cố: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 4”, \(B\) là biến cố “Tích số chấm xuất hiện trên hai con xúc xắc bằng 4”. Tập hợp mô tả biến cố \(AB\) là
A. \(\left\{ {\left( {2;2} \right)} \right\}\).
B. \(\left\{ {\left( {1;3} \right),\left( {3;1} \right),\left( {2;2} \right)} \right\}\).
C. \(\left\{ {\left( {1;3} \right),\left( {3;1} \right)} \right\}\).
D. \(\left\{ {\left( {3;1} \right),\left( {2;2} \right)} \right\}\).
Với \(a\) là số thực dương tùy ý, \(\sqrt[{14}]{a}\) bằng
A. \({a^{\frac{1}{{14}}}}\).
B. \({a^{\sqrt {14} }}\).
C. \({a^{14}}\).
D. \(\sqrt {{a^{14}}} \).
Cho \(a,b\) là các số thực dương tùy ý. Khẳng định nào sau đây là đúng?
A. \(\ln \left( {a + b} \right) = \ln a.\ln b\).
B. \(\ln \left( {a + b} \right) = \ln a + \ln b\).
C. \(\ln \left( {ab} \right) = \ln a + \ln b\).
D. \(\ln \left( {ab} \right) = \ln a.\ln b\).
Với hai số thực dương \(a,b\) tùy ý và \(\frac{{{{\log }_3}5.{{\log }_5}a}}{{1 + {{\log }_3}2}} - {\log _6}b = 2\). Khẳng định nào dưới đây là khẳng định đúng?
A. \(a = 36b\).
B. \(a = b{\log _6}3\).
C. \(2a + 3b = 0\).
D. \(a = b{\log _6}2\).
Có bao nhiêu số nguyên thuộc tập xác định của hàm số \(y = \log \left[ {\left( {6 - x} \right)\left( {x + 2} \right)} \right]\)?
A. \(7\).
B. \(8\).
C. Vô số.
D. \(9\).
Cho \({4^x} + {4^{ - x}} = 7\). Biểu thức \(P = \frac{{5 + {2^x} + {2^{ - x}}}}{{8 - {{4.2}^x} - {{4.2}^{ - x}}}}\) có giá trị bằng
A. \(P = \frac{3}{2}\).
B. \(P = - \frac{5}{2}\).
C. \(P = 2\).
D. \(P = - 2\).
Cho hình chóp \(S.ABCD\) có đáy là hình vuông. Gọi \(M,N\) lần lượt là trung điểm của \(SA\) và \(SC\).
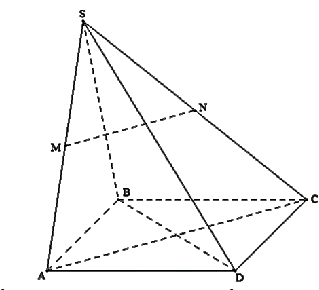
Chọn khẳng định đúng trong các khẳng định sau:
A. \(MN \bot BD\).
B. \(MN \bot SD\).
C. \(MN \bot SA\).
D. \(MN \bot SB\).
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(B\) và \(SA \bot \left( {ABC} \right)\).
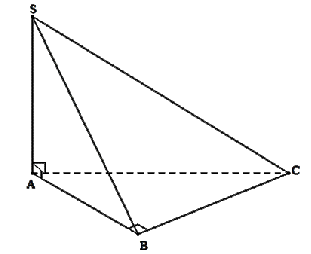
Hình chiếu của \(SC\) lên \(\left( {ABC} \right)\) là
A. \(SB\).
B. \(BC\).
C. \(AB\).
D. \(AC\).
Cho \(A\) và \(B\) là hai biến cố độc lập. Biết \(P\left( A \right) = 0,4\) và \(P\left( B \right) = 0,5\). Xác suất của biến cố \(A \cup B\) là:
A. \(0,9\).
B. \(0,7\).
C. \(0,5\).
D. \(0,2\).
Hai mái nhà trong hình là hai hình chữ nhật, biết \(AB = AC = 2,8{\rm{m}}\), \(BC = 5{\rm{m}}\). Số đo góc nhị diện tạo bởi hai nửa mặt phẳng chứa hai mái nhà đó bằng bao nhiêu?
A. \(125^\circ \).
B. \(126^\circ 28'\).
C. \(130^\circ 30'\).
D. \(150^\circ \).
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
