12 CÂU HỎI
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau:
Mẫu số liệu được chia thành bao nhiêu nhóm?
A. 6 nhóm.
B. 5 nhóm.
C. 7 nhóm.
D. 8 nhóm.
Chọn ngẫu nhiên một học sinh trong lớp. Gọi \(A\) là biến cố: “Bạn đó là học sinh giỏi Toán”; \(B\) là biến cố: “Bạn đó là học sinh giỏi Văn”. Khi đó, biến cố \(A \cup B\) là:
A. Bạn đó là học sinh giỏi cả Văn và Toán.
B. Bạn đó là học sinh giỏi Văn hoặc giỏi Toán.
C. Bạn đó là học sinh giỏi Văn nhưng không giỏi Toán.
D. Bạn đó là học sinh giỏi Toán nhưng không giỏi Văn.
Quãng đường (km) các cầu thủ (không tính thủ môn) chạy trong một trận bóng đá tại giải ngoại hạng Anh được cho trong bảng thống kê sau:
Tính quãng đường trung bình một cầu thủ chạy trong trận đấu này.
A. \(7,25\).
B. \(8,23\).
C. \(7,48\).
D. \(7,67\).
Cho a là một số thực dương, biểu thức \({a^{\frac{2}{3}}}\sqrt a \)viết dưới dạng lũy thừa với số mũ hữu tỉ là
A. \({a^{\frac{5}{6}}}\).
B. \({a^{\frac{7}{6}}}\).
C. \({a^{\frac{{11}}{6}}}\).
D. \({a^{\frac{6}{5}}}\).
Cho \(a > 0,\,a \ne 1\), biểu thức \(D = {\log _{{a^3}}}a\) có giá trị bằng bao nhiêu?
A. \( - 3\).
B. \(3\).
C. \(\frac{1}{3}\).
D. \( - \frac{1}{3}\).
Mệnh đề nào đúng trong các mệnh đề sau?
A. Góc giữa hai đường thẳng bằng góc giữa hai vectơ chỉ phương của hai đường thẳng đó.
B. Góc giữa hai đường thẳng là góc nhọn.
C. Góc giữa hai đường thẳng \[a\] và \[b\] bằng góc giữa hai đường thẳng \[a\] và \[c\] khi \[b\] song song với \[c\] (hoặc \[b\] trùng với \[c\]).
D. Góc giữa hai đường thẳng \[a\] và \[b\] bằng góc giữa hai đường thẳng \[a\] và \[c\] thì \[b\] song song với \[c\].
Qua \(O\) cho trước, có bao nhiêu mặt phẳng vuông góc với đường thẳng \(\Delta \) cho trước?
A. \(1\).
B. Vô số.
C. \(3\).
D. \(2\).
Cho \(A,B\) là hai biến cố độc lập cùng liên quan đến phép thử \(T\), xác suất xảy ra biến cố \(A\) là \(\frac{1}{2}\), xác suất xảy ra biến cố \(B\) là \(\frac{1}{4}\). Xác suất để xảy ra biến cố \(A\) và \(B\) là:
A. \(P\left( {AB} \right) = \frac{1}{8}\).
B. \(P\left( {AB} \right) = \frac{3}{4}\).
C. \(P\left( {AB} \right) = \frac{1}{4}\).
D. \(P\left( {AB} \right) = \frac{7}{8}\).
Cho đồ thị hai hàm số \(y = {a^x}\) và \(y = {\log _b}x\) như hình vẽ
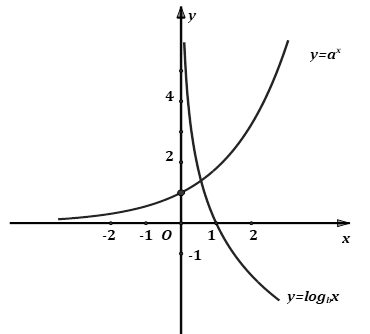
A. \(a > 1;b > 1\).
B. \(a > 1;0 < b < 1\).
C.(0 < a < 1;0 < b < 1\).
D. \(0 < a < 1;b > 1\).
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B,\) cạnh bên \(SA\) vuông góc với đáy. Gọi \(H\) là chân đường cao kẻ từ \(A\) của tam giác \(SAB\). Khẳng định nào dưới đây là sai?
A. \(SA \bot BC\).
B. \(AH \bot BC\).
C. \(AH \bot AC\).
D. \(AH \bot SC\).
Cường độ một trận động đất M (richter) được cho bởi công thức \(M = \log A - \log {A_0}\), với \(A\) là biên độ rung chấn tối đa và \({A_0}\) là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San Francisco có cường độ 8 độ Richter. Trong cùng năm đó, trận động đất khác Nam Mỹ có biên độ mạnh hơn gấp 4 lần. Cường độ của trận động đất ở Nam Mỹ gần với số nào sau đây nhất là
A. \(8,9\).
B. \(7,9\).
C. \(8,6\).
D. \(8,4\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, cạnh bên \(SA\) vuông góc với đáy. Tính diện tích hình chiếu của \(\Delta SBC\) trên mặt phẳng \(\left( {SAC} \right)\) biết \(SA = AB = 2a;AD = a\).
A. \({a^2}\sqrt 2 \).
B. \(\frac{{{a^2}\sqrt 5 }}{2}\).
C. \({a^2}\).
D. \(\frac{{{a^2}\sqrt 5 }}{5}\).
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải