50 CÂU HỎI
Hai đường tiệm cận của đồ thị hàm số \(y = \frac{{2x - 1}}{{x + 2}}\) là:
A. \(x = - 2;\,\,\,y = - 2\)
B. \(x = - 2;\,\,\,y = \frac{1}{2}\)
C. \(x = - 2;\,\,\,y = 2\)
D. \(x = 2;\,\,\,y = 2\)
Biết đường thẳng \(y = x + 1\) cắt đồ thị hàm số \(y = \frac{{2x + 1}}{{x - 1}}\) tại hai điểm phân biệt A, B có hoành độ lần lượt là \({x_A},\,{x_B}\). Tính giá trị của \({x_A} + {x_B}\).
A. \({x_A} + {x_B} = 2\)
B. \({x_A} + {x_B} = - 2\)
C. \({x_A} + {x_B} = 0\)
D. \({x_A} + {x_B} = 1\)
Tìm tập xác định D của hàm số \(y = {\log _2}\left( { - {x^2} + 3x} \right)\)
A. \(D = \mathbb{R}\)
B. \(D = \mathbb{R}\backslash \left( {0;3} \right)\)
C. \(\left( { - \infty ;0} \right) \cup \left( {3; + \infty } \right)\)
D. \(D = \left( {0;3} \right)\)
Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị?
A. \(y = {x^4}\)
B. \(y = {x^2} + 2x + 2\)
C. \(y = \frac{{x - 1}}{{x + 3}}\)
D. \(y = - {x^3} + x\)
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số \(y = \frac{x}{{x - m\sqrt {4 - {x^2}} }}\) có ba tiệm cận đứng.
A. \( - 2 < m < 2\)
B. \(\left\{ \begin{array}{l}m \ne 0\\ - 2 < m < 2\end{array} \right.\)
C. Mọi giá trị m.
D. \( - 2 \le m \le 2\)
Trong không gian Oxyz, cho bốn điểm \(A\left( {1;0;0} \right),\,\,B\left( {0;2;0} \right),\,\,C\left( {0;0;3} \right),\,\,D\left( {1;2;3} \right)\). Phương trình mặt cầu đi qua bốn điểm A, B, C, D là:
A. \({x^2} + {y^2} + {z^2} - x - 2y - 3z = 0\)
B. \({x^2} + {y^2} + {z^2} - x - 2y - 3z - 14 = 0\)
C. \({x^2} + {y^2} + {z^2} - x - 2y - 3z - 6 = 0\)
D. \({x^2} + {y^2} + {z^2} - 2x - 4y - 6z = 0\)
Cho hàm số \(y = \frac{{2x - 1}}{{x - 2}}\). Khẳng định nào dưới đây đúng?
A. Đồ thị hàm số có tiệm cận đứng là \(x = 2\)
B. Hàm số có tiệm cận đứng là \(x = 2\)
C. Đồ thị hàm số không có tiệm cận.
D. Đồ thị hàm số có tiệm cận ngang \(y = \frac{1}{2}\)
Tìm tập nghiệm S của phương trình \({4^x} - {6.2^x} + 8 = 0\)
A. \(S = \left( {1;2} \right)\)
B. \(S = \left\{ 2 \right\}\)
C. \(S = \left\{ 1 \right\}\)
D. \(S = \left\{ {1;2} \right\}\)
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A, B, \(AB = BC = a,\,\,SA = AD = 2a\), gọi E là trung điểm của AD. Tính bán kính R của mặt cầu ngoại tiếp khối chóp S.CDE theo a.
A. \(R = \frac{{3a\sqrt 2 }}{2}\)
B. \(R = \frac{{a\sqrt 5 }}{2}\)
C. \(R = \frac{{a\sqrt {11} }}{2}\)
D. \(R = \frac{{a\sqrt 2 }}{2}\)
Cho hàm số \(y = \frac{1}{2}{x^2}{e^x}\). Giá trị biểu thức \(y'' - 2y' + y\) tại \(x = 0\) là:
A. 1
B. e
C. 0
D. \(\frac{1}{e}\)
Trong các hình hộp chữ nhật nằm trong mặt cầu bán kính R, thể tích lớn nhất có thể của khối hộp chữ nhật là
A. \(\frac{{4{R^3}\sqrt 3 }}{2}\)
B. \(\frac{{8{R^3}\sqrt 3 }}{9}\)
C. \(\frac{{16{R^3}\sqrt 3 }}{3}\)
D. \(\frac{{8{R^3}\sqrt 3 }}{3}\)
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = {x^3} - 3x + 2\) tại giao điểm của đồ thị hàm số với trục tung.
A. \(y = 2\)
B. \(y = - 3x + 2\)
C. \(y = 3x + 2\)
D. \(y = - 3x - 2\)
Tìm tất cả các giá trị thực của tham số m để phương trình \({4^x} - {2^{x + 3}} + 3 = m\) có đúng 2 nghiệm thực phân biệt trong khoảng \(\left( {1;3} \right)\).
A. \( - 13 < m < - 9\)
B. \( - 9 < m < 3\)
C. \( - 13 < m < 3\)
D. \(3 < m < 9\)
Tìm tất cả các giá trị thực của tham số m để phương trình \({x^3} - {3^2} - m = 0\) có hai nghiệm phân biệt.
A. Không có m.
B. \(m \in \left\{ {0;4} \right\}\)
C. \(m \in \left\{ { - 4;0} \right\}\)
D. \(m = 0\)
Đồ thị hàm số \(y = \frac{{\sqrt {9 - {x^2}} }}{{{x^2} - 6x + 8}}\) có bao nhiêu đường tiệm cận?
A. 4
B. 3
C. 2
D. 1
Giá trị thực của tham số m để đồ thị hàm số \(y = {x^4} - 2m{x^2} + m\) có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ làm trọng tâm là
A. \(m = 1\)
B. Không có m.
C. \(m = \frac{3}{2}\)
D. \(m = \frac{1}{2}\)
Hàm số \(y = {x^4} - 2017{x^2} + 2018\) có giá trị cực đại là
A.
B.
C.
D.
liên tục trên R và có đạo hàm được xác định hàm số bởi hàm số \(f'\left( x \right) = {x^2}{\left( {x - 1} \right)^3}\left( {x + 3} \right)\). Hỏi đồ thị hàm số \(y = f\left| x \right|\) có bao nhiêu điểm cực trị?
A. 0
B. 3
C. 2
D. 1
Cho hình trụ có diện tích toàn phần lớn hơn diện tích xung quanh là \(4\pi \). Bán kính đáy của hình trụ là
A. \(\frac{{\sqrt 2 }}{2}\)
B. 2
C. \(\sqrt 2 \)
D. 1
Tìm tập xác định D của hàm số \(y = {\left( {{x^2} - 1} \right)^{ - 3}}\)
A. \(D = \left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\)
B. \(D = \emptyset \)
C. \(D = R\)
D. \(D = R\backslash \left\{ { \pm 1} \right\}\)
Trong không gian Oxyz, cho hai điểm \(A\left( {1;2;0} \right),\,\,\,B\left( {2; - 1;1} \right)\). Tìm điểm C có hoành độ dương trên trục Ox sao cho tam giác ABC vuông tại C.
A. \(C\left( {3;0;0} \right)\)
B. \(C\left( {2;0;0} \right)\)
C. \(C\left( {1;0;0} \right)\)
D. \(C\left( {5;0;0} \right)\)
Trong không gian Oxyz, cho hai điểm \(A\left( {1;2; - 2} \right),\,\,B\left( {2; - 1;2} \right)\). Tìm tọa độ điểm M trên mặt phẳng Oxy sao cho \(MA + MB\) đạt giá trị nhỏ nhất.
A. \(M\left( {1;1;0} \right)\)
B. \(M\left( {\frac{3}{2};\frac{1}{2};0} \right)\)
C. \(M\left( {2;1;0} \right)\)
D. \(M\left( {\frac{1}{2};\frac{3}{2};0} \right)\)
Tập nghiệm của bất phương trình \({2^{x + 2}} < {\left( {\frac{1}{4}} \right)^{ - x}}\) là
A. \(S = \left( {1; + \infty } \right)\)
B. \(S = \left( { - \infty ;1} \right)\)
C. \(S = \left( { - \infty ;2} \right)\)
D. \(S = \left( {2; + \infty } \right)\)
Số điểm cực trị của hàm số \(y = {x^4} - 3{x^2} + 5\) là:
A. 3
B. 1
C. 2
D. 0
Giải phương trình \({\log _3}\left( {x - 1} \right) = 2\)
A. \(x = 8\)
B. \(x = 10\)
C. \(x = 7\)
D. \(x = 9\)
Số chữ số của số tự nhiên \(N = {3^{2017}}\) là:
A. 962
B. 964
C. 961
D. 963
Cho hàm số \(y = f\left( x \right) = {e^{\frac{1}{{x\left( {x + 1} \right)}}}}\). Tính giá trị biểu thức \(T = f\left( 1 \right).f\left( 2 \right).f\left( 3 \right)...f\left( {2017} \right).\sqrt[{2018}]{e}\)
A. \(T = 1\)
B. \(T = e\)
C. \(T = \frac{1}{e}\)
D. \(T = {e^{\frac{1}{{2018}}}}\)
Cho khối hộp ABCD.A’B’C’D’ có thể tích là 36. Tính thể tích V của khối chóp A.CB’D’.
A. \(V = 18\)
B. \(V = 6\)
C. \(V = 9\)
D. \(V = 12\)
Cho hình chóp S.ABCD có cạnh bên SA tạo với đáy một góc \({60^0}\) và \(SA = a\sqrt 3 \), đáy là tứ giác có hai đường chéo vuông góc, \(AC = BD = 2a\). Tính thể tích V của khối chóp theo a.
A. \(V = \frac{{2{a^3}\sqrt 3 }}{3}\)
B. \(V = 3{a^3}\)
C. \(V = {a^3}\)
D. \(V = \frac{{3{a^3}}}{2}\)
Hàm số \(y = {x^3} - 3x\) đồng biến trên khoảng nào?
A. \(\left( {1;1} \right)\)
B. \(\left( { - \infty ; - 1} \right)\)
C. \(\left( { - \infty ; + \infty } \right)\)
D. \(\left( {0; + \infty } \right)\)
Cho bất phương trình \({2^{{x^2} + x}} + 2x \le {2^{3 - x}} - {x^2} + 3\) có tập nghiệm là \(\left[ {a;b} \right]\). Giá trị của \(T = 2a + b\) là:
A. \(T = 1\)
B. \(T = - 5\)
C. \(T = 3\)
D. \(T = - 2\)
Cho hàm số \(y = \frac{{mx - 1}}{{x - n}}\), trong đó m, n là tham số. Biết giao điểm của hai đường tiệm cận của đồ thị hàm số nằm trên đường thẳng \(x - 2y + 3 = 0\) và đồ thị hàm số đi qua điểm \(A\left( {0;1} \right)\). Giá trị của \(m + n\) là:
A. \(m + n = - 3\)
B. \(m + n = 3\)
C. \(m + n = 1\)
D. \(m + n = - 1\)
Biết rằng hàm số \(y = f\left( x \right) = {x^3} + a{x^2} + bx + c\) đạt cực tiểu tại điểm \(x = 1\), giá trị cực tiểu bằng –3 và đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2. Tính giá trị của hàm số tại \(x = 2\).
A. \(f\left( 2 \right) = 8\)
B. \(f\left( 2 \right) = 0\)
C. \(f\left( 2 \right) = 6\)
D. \(f\left( 2 \right) = 4\)
Cho phương trình \({\left( {\frac{{\tan \frac{\pi }{{12}}}}{{1 - \tan \frac{\pi }{{12}}}}} \right)^{\frac{x}{{2017}}}} + \frac{{\sqrt[4]{{12}}\tan \frac{\pi }{{12}}}}{{1 - \tan \frac{\pi }{{12}}}}.{\left( {\frac{{\tan \frac{\pi }{{12}}}}{{1 + \tan \frac{\pi }{{12}}}}} \right)^{\frac{x}{{2017}}}} = 2017.{\left( {\frac{1}{{2\sqrt 3 }}} \right)^{\frac{x}{{4034}}}}\). Tính tổng tất cả các nghiệm thực của phương trình đã cho.
A. 0
B. 1
C. –1
D. 2017
Tính thể tích V khối lập phương biết rằng khối cầu ngoại tiếp khối lập phương có thể tích là \(\frac{{32}}{3}\pi \)
A. \(V = \frac{{64\sqrt 3 }}{9}\)
B. \(V = 8\)
C. \(V = \frac{{8\sqrt 3 }}{9}\)
D. \(V = \frac{{8\sqrt 3 }}{3}\)
Hàm số nào trong bốn hàm số liệt kê ở dưới đồng biến trên các khoảng xác định của hàm số.
A. \(y = {\left( {\frac{\pi }{e}} \right)^{2x + 1}}\)
B. \(y = {3^{ - x}}\)
C. \(y = {\left| {\sin 2017} \right|^x}\)
D. \(y = {\left( {\frac{2}{e}} \right)^x}\)
Cho hàm số \(y = {x^3} - 3{x^2} + 2\). Gọi A, B là 2 điểm thuộc đồ thị hàm số đã cho có hoành độ lần lượt là \({x_A},\,{x_B}\), tiếp tuyến của đồ thị hàm số tại A, B song song với nhau và đường thẳng AB tạo với 2 trục tọa độ một tam giác cân, đường thẳng AB có hệ số góc dương. Tính \({x_A}{x_B}\).
A. \({x_A}{x_B} = - 1\)
B. \({x_A}{x_B} = - 3\)
C. \({x_A}{x_B} = - 2\)
D. \({x_A}{x_B} = 2\)
Tiếp tuyến với đồ thị \(y = \frac{{2x - 1}}{{x - 2}}\) tại điểm có tung độ bằng 5 có hệ số góc k là
A. \(k = - \frac{1}{3}\)
B. \(k = - 1\)
C. \(k = - 3\)
D. \(k = \frac{1}{3}\)
Cho hình nón tròn xoay có đường cao \(h = 4\) và diện tích đáy là \(9\pi \). Tính diện tích xung quanh của hình nón.
A. \({S_{xq}} = 10\pi \)
B. \({S_{xq}} = 15\pi \)
C. \({S_{xq}} = 25\pi \)
D. \({S_{xq}} = 30\pi \)
Tìm giá trị nhỏ nhất của hàm số \(y = x + 1 + \frac{4}{x}\) trên \(\left[ {1;3} \right]\)
A. \(\mathop {\min }\limits_{x \in \left[ {1;3} \right]} y = 4\)
B. \(\mathop {\min }\limits_{x \in \left[ {1;3} \right]} y = 5\)
C. \(\mathop {\min }\limits_{x \in \left[ {1;3} \right]} y = \frac{{16}}{3}\)
D. \(\mathop {\min }\limits_{x \in \left[ {1;3} \right]} y = 6\)
Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số dưới đây?
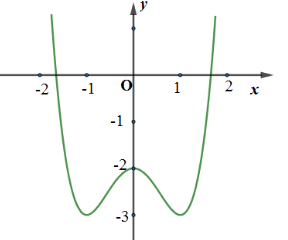
A. \(y = {x^3} - 3x - 2\)
B. \(y = {x^4} - 2{x^2} - 2\)
C. \(y = - {x^4} + 2{x^2} - 2\)
D. \(y = {x^4} + 2{x^2} - 2\)
Tập nghiệm của bất phương trình \({\log _{\frac{1}{2}}}\left( {x - 3} \right) \ge {\log _{\frac{1}{2}}}\left( {9 - 2x} \right)\) là:
A. \(S = \left( {3;4} \right)\)
B. \(S = \left( { - \infty ;4} \right]\)
C. \(S = \left( {3;\frac{9}{2}} \right)\)
D. \(S = \left( {3;4} \right]\)
Diện tích toàn phần của một hình hộp chữ nhật là \({S_{tp}} = 8{a^2}\). Đáy của hình hộp là hình vuông cạnh a. Tính thể tích V của khối hộp theo a.
A. \(V = 3{a^3}\)
B. \(V = {a^3}\)
C. \(V = \frac{{3{a^3}}}{2}\)
D. \(V = \frac{7}{4}{a^3}\)
Trong không gian Oxyz, phương trình mặt cầu tâm \(T = \left( { - 1;2;0} \right)\) và đi qua điểm \(A\left( {2; - 2;0} \right)\) là
A. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {z^2} = 100\)
B. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {z^2} = 5\)
C. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {z^2} = 10\)
D. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {z^2} = 25\)
Tìm tập hợp tất cả các giá trị của tham só thực m để hàm số \(y = \frac{{mx - 1}}{{x - m}}\) đồng biến trên từng khoảng xác định:
A. \(\left( { - \infty ; - 1} \right)\)
B. \(\left( { - 1;1} \right)\)
C. \(\left( {1; + \infty } \right)\)
D. \(\left( { - \infty ;1} \right)\)
Hình nón có chiều cao bằng đường kính đáy. Tỉ số thể tích giữa diện tích xung quanh và diện tích toàn phần của hình nón là:
A. \(\frac{1}{2}\)
B. \(\frac{{1 + \sqrt 5 }}{4}\)
C. \(\frac{1}{4}\)
D. \(\frac{{5 - \sqrt 5 }}{4}\)
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, \(SA = a\) và vuông góc với đáy. Thể tích V của khối chóp S.ABC theo a là:
A. \({V_{S.ABC}} = \frac{{{a^3}\sqrt 3 }}{{12}}\)
B. \({V_{S.ABC}} = \frac{{{a^3}\sqrt 2 }}{{12}}\)
C. \({V_{S.ABC}} = \frac{{{a^3}\sqrt 3 }}{3}\)
D. \({V_{S.ABC}} = \frac{{{a^3}\sqrt 3 }}{4}\)
Đạo hàm của hàm số \(y = {\log _2}\left( {{x^2} - 2x} \right)\) là:
A. \(y' = \frac{1}{{\left( {{x^2} - 2x} \right)\ln 2}}\)
B. \(y' = \frac{{x - 1}}{{{x^2} - 2x}}\)
C. \(y' = \frac{{x - 1}}{{\left( {{x^2} - 2x} \right)\ln 2}}\)
D. \(y' = \frac{1}{{\left( {{x^2} - 2x} \right)\ln \sqrt 2 }}\)
Trong không gian Oxyz, cho ba vectơ \(\overrightarrow a \left( {1;2;1} \right),\,\,\overrightarrow b \left( {0;2; - 1} \right),\,\,\overrightarrow c \left( {m;1;0} \right)\). Tìm giá trị thực của tham số m để ba vectơ \(\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c \) đồng phẳng.
A. \(m = 1\)
B. \(m = 0\)
C. \(m = \frac{{ - 1}}{4}\)
D. \(m = \frac{1}{4}\)
Khối cầu có thể tích là \(36\pi \). Diện tích xung quanh của mặt cầu là
A. \({S_{xq}} = 9\pi \)
B. \({S_{xq}} = 27\pi \)
C. \({S_{xq}} = 18\pi \)
D. \({S_{xq}} = 36\pi \)

