Bộ 24 Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 22)

Tính tổng $S=0,3+{\left(0,3\right)}^2+{\left(0,3\right)}^3+\mathrm{....}+{\left(0,3\right)}^n+\mathrm{...}$

Cho phương trình $x^5-7x^4+3x^2+2=0$. Mệnh đề nào sau đây là đúng?

Tìm khẳng định đúng:

Biết $\underset{x\to -1^{+}}{\lim }\frac{3x+a}{x+1}=-\infty$ thì giá trị của a thỏa mãn:

Cho $\lim \frac{\sqrt{8n^2+1}+4-3n}{n+3}=a\sqrt{2}+b$. Mệnh đề nào đúng?

Tìm hệ thức liên hệ giữa a  và b để $\lim \left(\sqrt{n^2+an+3}-\sqrt{n^2+bn-1}\right)=1$.

Cho tứ diện đều ABCD , M là trung điểm của cạnh AB . Khi đó góc giữa hai vec tơ $\overrightarrow{AB},\overrightarrow{CM}$ .

Chọn mệnh đề đúng?  Trong không gian:

Cho hình chóp SABC có $SA\perp \left(ABC\right)$ và $AB\perp BC$. H là hình chiếu vuông góc của A lên SB. Khẳng định nào sau đây là đúng?

Tính giới hạn của dãy số $u_n=\frac{1}{2\sqrt{1}+\sqrt{2}}+\frac{1}{3\sqrt{2}+2\sqrt{3}}+\mathrm{...}+\frac{1}{\left(n+1\right)\sqrt{n}+n\sqrt{n+1}}$:

Dãy số nào sau đây có giới hạn bằng 0?

Cho các khẳng định:

(I): Cho hàm số y= f(x)  liên tục trên [a,b] và $f\left(a\right).f\left(b\right)<0$. Khi đó phương trình $f\left(x\right)=0$ có ít nhất một nghiệm trên khoảng (a,b).

(II): Cho hàm số $y=f\left(x\right)$ liên tục trên [a,b] và $f\left(a\right).f\left(b\right)>0$. Khi đó phương trình f(x)=0 không có nghiệm trên khoảng (a,b).

Trong các khẳng định trên:

Cho hàm số f(x)  có đồ thị như hình vẽ

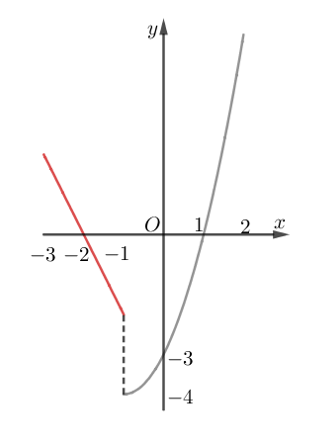Chọn đáp án đúng

Cho hình hộp ABCDA'B'C'D'. Một đường thẳng $∆$ cắt các đường thẳng AA', BC, C'D' lần lượt tại M, N,P sao cho $\overrightarrow{NM}=3\overrightarrow{NP}$. Tính $k=\frac{MA}{M{A}^{\text{'}}}$?

Cho $\overrightarrow{u},\overrightarrow{v}$ bất kì, chọn mệnh đề đúng?

$\lim \left(4-n^{2018}-n^{2019}\right)$ bằng 

Cho hình chóp tứ giác SABCD có đáy ABCD là hình vuông cạnh a, các cạnh bên đều bằng $a\sqrt{2}$. Góc giữa cạnh bên SB và (ABCD) bằng:

Rút gọn $S=1+{\sin }^{2}x+{\sin }^{4}x+{\sin }^{6}x+\mathrm{...}+{\sin }^{2n}x+\mathrm{...}$với $\sin x\ne \pm 1$.

$\underset{x\to +\infty }{\lim }\left(\sqrt{x+\sqrt{3x+\sqrt{5x+\sqrt{7x+\mathrm{...}+\sqrt{2019x}}}}}-\sqrt{x}\right)=\frac{\sqrt{a}}{b}$ (với a,b nguyên dương nhỏ nhất). Tính a+b.

Tìm a  để hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{x^2-3x+2}{x-2}\text{ khi x < 2}\\ ax+a-5\text{ khi x}\ge \text{2}\end{array}\right.$ liên tục trên R

Cho hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{\sqrt{x+1}-1}{x}\text{ khi }x\ne 0\\ \frac{1}{2}\text{ khi x = 0}\end{array}\right.$. Chọn khẳng định đúng?

Cho hình chóp SABC có SA=SC=AB=AC= $a\sqrt{2}$ và BC=2a. Khi đó góc giữa hai đường thẳng AC và SB.

Cho hình chóp SABCD có đáy là hình vuông ABCD và SA vuông góc với mặt phẳng đáy (ABCD). Một mặt phẳng$\left(\alpha \right)$ qua A vuông góc với SC cắt hình chóp với thiệt diện là:

Cho tứ diện ABCD. Gọi M,N,G lần lượt là trung điểm của AB, CD và MN. Chọn khẳng định đúng:

$\underset{x\to 1}{\lim }\frac{\sqrt[3]{5x+3}-\sqrt{x+3}}{x^2-1}=\frac{5}{m}-\frac{1}{n}$ (với m,n là các số nguyên dương). Tính  m-n ?

Cho hình lập phương ABCDEFGH. Hãy xác định góc giữa cặp vectơ $\overrightarrow{AC}$ và $\overrightarrow{DE}$?

$\underset{x\to 3^{-}}{\lim }\frac{x+5}{x-3}$ bằng

Cho tứ diện ABCD đều cạnh bằng a . Góc giữa AB và CD bằng.

Tìm m  để hàm số: $y=\left\{\begin{array}{l}x+2m\begin{array}{ccc}& \begin{array}{cc}khi& x<0\end{array}& \end{array}\\ x^2+x+1\begin{array}{ccc}& \begin{array}{cc}khi& x\ge 0\end{array}& \end{array}\end{array}\right.$liên tục tại x=0.

$\underset{x\to +\infty }{\lim }x\left(\sqrt{x^2+3}-x\right)$ bằng 

Tìm khẳng định sai trong các khẳng định sau:

$\underset{x\to \sqrt{3}}{\lim }\left(x^2-4\right)$ bằng 

Cho lăng trụ tam giác ABCA'B'C' có $\overrightarrow{A{A}^{\text{'}}}=\overrightarrow{a}$, $\overrightarrow{AB}=\overrightarrow{b}$, $\overrightarrow{AC}=\overrightarrow{c}$. Hãy biểu diễn vectơ $\overrightarrow{B^{\text{'}}C}$ theo các vectơ $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$.

$\underset{x\to 0}{\lim }\frac{\left(1+x\right)\left(1+2x\right)\left(1+3x\right)\mathrm{...}\left(1+2019x\right)-1}{x}$ bằng 

Biết hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{x^2+ax+b}{x^2-1}\text{ khi }x\ne 1\\ \frac{-1}{2}\text{ khi }x=1\end{array}\right.\left(a;b\in ℝ\right)$ liên tục tại x=1 . Hãy tính $S=2a+5b$.

$\underset{x\to 1}{\lim }\frac{x^2-3x+2}{x-1}$ bằng 

Cho f(x) liên tục trên [-1,5] thỏa mãn f(-1)=1, f(5)= 6. Phương trình nào sau đây luôn có nghiệm trong khoảng (1,-5) ?

Giá trị của $\lim \left(\sqrt{4n^2+5n+1}-2n\right)$ bằng :

$\underset{x\to -\infty }{\lim }\left(5-3x^2-2019x^4\right)$ bằng 

Cho hình chóp SABCD có đáy ABCD là hinh thoi tâm O . Biết SA=SC, SB=SD. Khẳng định nào sau đây sai?

Cho hình chóp ABCD có đáy ABC là tam giác đều cạnh a. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. Biết $SO\perp \left(ABC\right),SO=2a$. Gọi M là điểm thuộc đường cao AH của tam giác ABC. Xét mặt phẳng (P) đi qua M và vuông góc với $AH,AM=x,x>\frac{a\sqrt{3}}{3}$. Xác định vị trí điểm M để thiết diện của hình chóp cắt bởi mặt phẳng (P) có điện tích lớn nhất. Khi đó $\frac{AM}{AH}$ bằng:

$\underset{x\to 0}{\lim }\frac{\sqrt{5x+3}-\sqrt{3}}{x}=\frac{a}{b\sqrt{c}}\left(a,c,c\in \mathbb{Z}\right)$ .Tính a-b+c

$\underset{x\to -\infty }{\lim }\left(-2018x^3+2x+5\right)$ bằng 

Hàm số $f\left(x\right)=\frac{x^2-4x+3}{x-2}$ không liên tục tại

$\underset{x\to -\infty }{\lim }\frac{1-3x}{2x+5}$ bằng 

Giá trị của $\lim \frac{2+3n}{3n^2-n+2}$ bằng:

Cho hai đường thẳng phân biệt a,b và điểm O không thuộc mặt phẳng (P). Mệnh đề nào sau đây là sai?

$\lim \frac{{10}^n+{30}^{n+2}}{{5.30}^n-{4.20}^n}$ bằng 

Cho hình chóp SABCD có đáy là hình vuông ABCD cạnh bằng a, $SA=a\sqrt{2}$ và SA vuông góc với mặt phẳng đáy ABCD. Gọi $\alpha$ là góc giữa SBvà mặt phẳng (SAC). Tính $\tan \alpha$?