Quiz

Bộ 24 Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 10)

Admin50 câu hỏiToánLớp 11

Bắt đầu ngay

50 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

. Cho tứ diện đều ABCD. Tính góc giữa hai véc-tơ $\vec{A B}$ và $\vec{B C}$

A. 60°;

B. 120°;

C. 30°;

D. 90°.

2. Nhiều lựa chọn

Cho hàm số $y = \frac{x^{2} + 1}{x^{2} + 5 x + 4} .$ Khi đó, hàm số liên tục trên khoảng nào sau đây?

A. (-3; 2);

B. (-¥; 3);

C. (-5; 3);

D. (-1; +¥).

3. Nhiều lựa chọn

Trong không gian cho ba đường thẳng a, b, c và mặt phẳng (a). Mệnh đề nào sau đây sai?

A. Nếu a // b và a ^ c thì b ^ c;

B. Nếu a ^ b và a ^ c, đồng thời b, c cắt nhau và b, c nằm trong (a) thì a ^ (a);

C. Nếu a ^ (a) thì a vuông góc với mọi đường thẳng nằm trong (a);

D. Nếu a ^ (a) và b ^ (a) thì a // b.

4. Nhiều lựa chọn

Cho tứ diện đều ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB và BC. Tính số đo góc giữa hai đường thẳng MN và CD.

A. 30°;

B. 60°;

C. 45°;

D. 90°.

5. Nhiều lựa chọn

Tính $\lim \frac{1}{n^{8}} .$

A. 1;

B. 0;

C. 2;

D. +¥.

6. Nhiều lựa chọn

Hàm số nào dưới đây gián đoạn tại điểm x₀ = -1.

A. $y = \frac{2 x - 1}{x + 1};$

B. $y = \frac{x}{x - 1};$

C. y = (x + 1)(x² + 2);

D. $y = \frac{x + 1}{x^{2} + 1} .$

7. Nhiều lựa chọn

$\lim_{x \to + \infty} \frac{2 x + 3}{x - 1}$ bằng

A. 0

B. 2

C. -1

D. -2

8. Nhiều lựa chọn

Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Khẳng định nào sau đây đúng?

A. $\vec{A G} = - \frac{1}{3} (\vec{A B} + \vec{A C} + \vec{A D});$

B. $\vec{A G} = \frac{1}{3} (\vec{A B} + \vec{A C} + \vec{A D});$

C. $\vec{A G} = \frac{2}{3} (\vec{A B} + \vec{A C} + \vec{A D});$

D. $\vec{A G} = - \frac{2}{3} (\vec{A B} + \vec{A C} + \vec{A D}) .$

9. Nhiều lựa chọn

Tính $\lim \frac{2 n + 1}{n - 1} .$

A. +¥;

B. -¥;

C. 2;

D. -1.

10. Nhiều lựa chọn

Tính $\lim_{x \to - \infty} (x^{3} + 3 x + 1) .$

A. 2;

B. 1;

C. -¥;

D. +¥.

11. Nhiều lựa chọn

Tính giới hạn $\lim_{x \to {(- 2)}^{-}} \frac{3 + 2 x}{x + 2}$

A. -¥;

B. 2;

C. +¥;

D. $\frac{3}{2} .$

12. Nhiều lựa chọn

Tìm $\lim_{x \to - 1} (x^{3} - 2 x^{2} + 1) .$

A. 0

B. 2;

C. -2;

D. -1.

13. Nhiều lựa chọn

Hàm số y = f (x) có đồ thị như hình bên. Hàm số gián đoạn tại điểmcó hoành độ bằng bao nhiêu?

Hàm số y = f (x) có đồ thị như hình bên. Hàm số gián đoạn tại điểm có hoành độ bằng bao nhiêu? (ảnh 1)

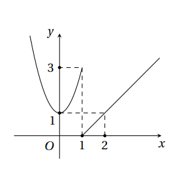
A. 0;

B. 2;

C. 3;

D. 1.

14. Nhiều lựa chọn

Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng BA’ và CD bằng

A. 90°;

B. 45°;

C. 30°;

D. 60°.

15. Nhiều lựa chọn

Trong hình hộp ABCD.A’B’C’D’ ba véc-tơ nào sau đây không đồng phẳng?

A. $\vec{A A'}, \vec{D D'}, \vec{C C'};$

B. $\vec{A B}, \vec{D D'}, \vec{D' C'};$

C. $\vec{A C'}, \vec{D D'}, \vec{A' C};$

D. $\vec{A B}, \vec{D D'}, \vec{B' C'} .$

16. Nhiều lựa chọn

Tính giới hạn $\lim_{x \to - \infty} \frac{x^{2} + 1}{x - 2} .$

A. 1

B. $- \frac{1}{2};$

C. +¥;

D. -¥.

17. Nhiều lựa chọn

Biết $\lim_{x \to 1} \frac{x^{2} - a x + 1}{x + 1} = 3.$ Khi đó giá trị của a là

A. -4;

B. 3;

C. 0;

D. 4.

18. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy là hình vuông và SA vuônggóc với đáy. Khẳng định nào sau đây đúng?

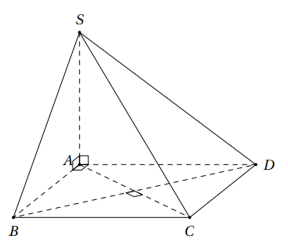
Cho hình chóp S.ABCD có đáy là hình vuông và SA vuông góc với đáy. Khẳng định nào sau đây đúng? (ảnh 1)

A. AC ^ (SCD);

B. BD ^ (SAD);

C. AC ^ (SBD);

D. BD ^ (SAC).

19. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và $S A = a \sqrt{2} .$ Số đo của góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng

A. 90°

B. 45°;

C. 60°

D. 30°.

20. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy là hình thoi tâm O và SO ^ (ABCD). Khi đó đườngthẳng AC vuông góc với mặt phẳng nào sau đây?

A. (SAB)

B. (SAD);

C. (SCD);

D. (SBD).

21. Nhiều lựa chọn

Cho hình lăng trụ ABC.A’B’C’, M là trung điểm của BB’. Đặt (Tham khảo hình vẽ).

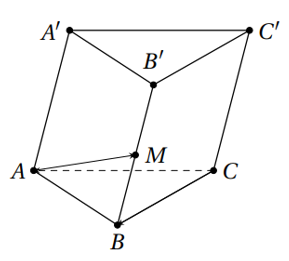
Cho hình lăng trụ ABC.A’B’C’, M là trung điểm của BB’. Đặt (Tham khảo hình vẽ). (ảnh 1)

Khẳng định nào sau đây đúng?

A. $\vec{A M} = \vec{b} + \vec{c} - \frac{1}{2} \vec{a};$

B. $\vec{A M} = \vec{b} - \vec{a} + \frac{1}{2} \vec{c};$

C. $\vec{A M} = \vec{a} + \vec{c} - \frac{1}{2} \vec{b};$

D. $\vec{A M} = \vec{a} - \vec{c} + \frac{1}{2} \vec{b} .$

22. Nhiều lựa chọn

Cho tứ diện ABCD với đáy BCD là tam giác vuông cân tại C. Các điểm M, N, P, Q lầnlượt là trung điểm của AB, AC, BC, CD. Góc giữa MN và PQ bằng

A. 45°;

B. 60°;

C. 30°

D. 0°.

23. Nhiều lựa chọn

Cho dãy số $u_{n} = n (\sqrt{n^{2} + 1} - n) .$ Khi đó limu_n bằng

A. +¥

B. 1;

C. 0;

D. $\frac{1}{2} .$

24. Nhiều lựa chọn

Giá trị của giới hạn $\lim_{x \to + \infty} (\sqrt{x^{2} + x + 1} - \sqrt{x^{2} - x + 1})$ là

A. 3;

B. 0;

C. 2;

D. 1.

25. Nhiều lựa chọn

Cho hình lập phương ABCD.A₁B₁C₁D₁. Góc giữa hai đường thẳng AC và DA₁ bằng

A. 120°;

B. 90°;

C. 60°;

D. 45°.

26. Nhiều lựa chọn

Tìm tất cả các giá trị của tham số a sao cho $\lim_{x \to a^{+}} \frac{- 2 x + 3}{x - a} = + \infty ?$

A. $a > \frac{3}{2};$

B. a > -1;

C. $a < \frac{3}{2};$

D. a < -1.

27. Nhiều lựa chọn

Tính $\lim \frac{1 + 19 n}{18 n + 19} .$

A. +¥;

B. $\frac{1}{19};$

C. $\frac{1}{18};$

D. $\frac{19}{18} .$

28. Nhiều lựa chọn

Cho tổng của một cấp số nhân lùi vô hạn $S = 1 - \frac{1}{3} + \frac{1}{9} - \frac{1}{27} + \frac{1}{81} - \cdot \cdot \cdot .$ Giá trị của S là

A. $S = - \frac{3}{4};$

B. $S = - \frac{4}{3};$

C. $S = \frac{3}{4};$

D. $S = \frac{4}{3} .$

29. Nhiều lựa chọn

Cho hàm số $f (x) = \{\begin{matrix} \frac{x - 8}{\sqrt[3]{x} - 2} k h i x > 8 \\ a x + 4 k h i x \leq 8 \end{matrix} .$ Để hàm số liên tục tại x = 8, giá trị

A. 2;.

B. 3;

C. 1;

D. 4

30. Nhiều lựa chọn

Trong bốn giới hạn sau đây, giới hạn nào bằng -¥?

A. $\lim_{x \to - \infty} \frac{- 3 x + 4}{x - 2};$

B. $\lim_{x \to 2^{+}} \frac{- 3 x + 4}{x - 2};$

C. $\lim_{x \to + \infty} \frac{- 3 x + 4}{x - 2};$

D. $\lim_{x \to 2^{-}} \frac{- 3 x + 4}{x - 2} .$

31. Nhiều lựa chọn

Cho hàm số $f (x) = \{\begin{matrix} \frac{x^{2} - 3 x + 2}{\sqrt{x + 2} - 2} k h i x > 2 \\ m^{2} x - 4 m + 6 k h i x \leq 2 \end{matrix},$ m là tham số. Có bao nhiêu giá trị của m để hàm số đã cho liên tục tại x = 2?

A. 0;

B. 2;

C. 1;

D. 3.

32. Nhiều lựa chọn

Cho hình chóp S.ABC có đáy là tam giác vuông tại B và SA ^ (ABC). Mệnh đề nào sauđây đúng?

A. Chỉ có đúng 2 mặt bên của hình chóp đã cho là các tam giác vuông;

B. Chỉ có đúng 1 mặt bên của hình chóp đã cho là tam giác vuông;

C. Cả 3 mặt bên của hình chóp đã cho là các tam giác vuông;

D. Không có mặt bên nào của hình chóp đã ho là tam giác vuông.

33. Nhiều lựa chọn

Tính $\lim \frac{{(2 n + 1)}^{6}}{{(n + 2)}^{4} {(2 n - 1)}^{2}} .$

A. $\frac{1}{16};$

B. 15

C. 8

D. 16

34. Nhiều lựa chọn

Tính $\lim_{x \to 3} \frac{x^{2} - 4 x + 3}{x^{2} - 9} .$

A. $\frac{1}{2};$

B. $\frac{2}{5};$

C. $\frac{1}{5};$

D. $\frac{1}{3};$

35. Nhiều lựa chọn

Cho hàm số $y = \{\begin{matrix} 2018 x + 2019 k h i x \geq - 1 \\ x + m k h i x < - 1 \end{matrix},$ m là tham số. Tìm m để hàm số liên tục trên ℝ.

A. m = 2;

B. m = -3;

C. m = 5;

D. m = 3.

36. Nhiều lựa chọn

Tính $I = \lim_{x \to + \infty} (\sqrt[3]{x^{3} + 2 x^{2}} - \sqrt{x^{2} - 2 x}) .$

A. $I = \frac{5}{3};$

B. I = 1

C. $I = \frac{2}{3};$

D. $I = \frac{1}{3} .$

37. Nhiều lựa chọn

Hình vẽ sau là đồ thị của một hàm số y = f (x). Hãy quan sát đồ thị và cho biết $\lim_{x \to {(- 1)}^{+}} f (x), \lim_{x \to {(- 1)}^{-}} f (x), \lim_{x \to + \infty} f (x), \lim_{x \to - \infty} f (x)$ lần lượt có giá trị bằng

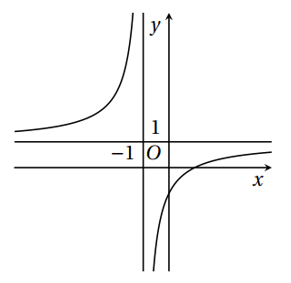
Hình vẽ sau là đồ thị của một hàm số y = f (x). Hãy quan (ảnh 1)

A. -¥, +¥, 1,1

B. 1, +¥, -¥, 1;

C. +¥, -¥, 1, 1;

D. 1, 1, +¥, -¥.

38. Nhiều lựa chọn

Có bao nhiêu giá trị của tham số m để $\lim_{x \to 2} \frac{\sqrt{x^{2} + 5} - 2 m}{x - 2} = \frac{1}{3} ?$

A. 2

B. 1

C. 0

D. 4

39. Nhiều lựa chọn

Cho dãy số (u_n) với $u_{n} = \sqrt{n^{2} + a n - 3} - \sqrt{n^{2} + n},$ trong đó a là tham số thực. Tìm a đểlimu_n = 3

A. 7

C. 4

C. 5

D. 6

40. Nhiều lựa chọn

Cho tứ diện ABCD có AB = CD = a. Gọi M và N lần lượt là trung điểm của AD và BC.Xác định độ dài đoạn thẳng MN để góc giữa hai đường thẳng AB và MN bằng 30°.

A. $M N = \frac{a}{4};$

B. $M N = \frac{a \sqrt{3}}{3};$

C. $M N = \frac{a \sqrt{3}}{2};$

D. $M N = \frac{a}{2} .$

41. Nhiều lựa chọn

Xét phương trình sau trên tập số thực x³ + x = a (1). Chọn khẳng định đúng trongcác khẳng định dưới đây?

A. Phương trình (1) chỉ có nghiệm khi x > a;

B. Phương trình (1) vô nghiệm khi x ³ a;

C. Phương trình (1) chỉ có nghiệm khi x ³ a;

D. Phương trình (1) có nghiệm "a Î ℝ

42. Nhiều lựa chọn

Cho hình chóp S.ABC có SA ^ (ABC) và $S A = a \sqrt{5},$ đáy là tam giác vuông tại A vớiAB = a, AC = 2a. Gọi a là góc giữa đường thẳng SA và mặt phẳng (SBC). Giá trị của tanabằng

A. $\frac{\sqrt{5}}{5};$

B. $\frac{2}{5};$

C. $\frac{2 \sqrt{5}}{5};$

D. 2

43. Nhiều lựa chọn

Cho hàm số $f (x) = \{\begin{matrix} 2 m x^{2} - 4 k h i x \leq 3 \\ 5 k h i x > 3 \end{matrix}$ m là tham số. Tìm m để hàm số liên tục trên ℝ

A. $\frac{1}{2};$

B. $\frac{1}{18};$

C. 18

D. 2

44. Nhiều lựa chọn

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-5; 5] để $L = \lim_{x \to + \infty} [x - 2 (m^{2} - 4) x^{3}] = - \infty ?$

A. 5

B. 10

C. 3

D. 6

45. Nhiều lựa chọn

Tìm giá trị của tham số a để hàm số $y = f (x) = \{\begin{matrix} \frac{x^{2} - 5 x + 6}{x - 3} k h i x \neq 3 \\ a k h i x = 3 \end{matrix}$

liên tục tại x = 3?

A. a = -1;

B. a = 0;

C. a = 2;

D. a = 1.

46. Nhiều lựa chọn

Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt $\vec{A A'} = \vec{a}, \vec{A B} = \vec{b}, \vec{A C} = \vec{c} .$ Khi đó bằng

A. $\vec{a} + \frac{1}{4} (\vec{b} + \vec{c});$

B. $\vec{a} + \frac{1}{2} (\vec{b} + \vec{c});$

C. $\vec{a} + \frac{1}{6} (\vec{b} + \vec{c});$

D. $\vec{a} + \frac{1}{3} (\vec{b} + \vec{c}) .$

47. Nhiều lựa chọn

Cho hình chóp S.ABCD có SA vuông góc với đáy và SA = 1, đáy là hình vuông cạnh x(0 < x £ 1). Tính giá trị lớn nhất của diện tích thiết diện của hình chóp đã cho khi cắt bởi mặtphẳng đi qua A và vuông góc với SC.

A. $\frac{\sqrt{6}}{15};$

B. $\frac{3 \sqrt{3}}{4};$

C. $\frac{\sqrt{3}}{5};$

D. $\frac{\sqrt{3}}{6} .$

48. Nhiều lựa chọn

Tính $\lim_{x \to 1} \frac{\sqrt[3]{26 + x} - \sqrt{x + 8}}{x^{2} - 3 x + 2} .$

A. $\frac{7}{54};$

B. $\frac{4}{27};$

C. $\frac{7}{55};$

D. $\frac{5}{54} .$

49. Nhiều lựa chọn

Cho hàm số $y = f (x) = \{\begin{matrix} \frac{\sqrt[3]{a x + 1} - \sqrt{1 - b x}}{x} k h i x \neq 0 \\ 3 a - 5 b - 1 k h i x = 0 \end{matrix} .$ Tìm điều kiện của tham số a, b để hàm số trên liên tục tại điểm x = 0. Khẳng định nào sau đây đúng?