20 CÂU HỎI
Trong không gian cho 10 điểm phân biệt, trong đó không có 4 điểm nào đồng phẳng. Số các hình tứ diện có thể kẻ được là:
A. 210.
B. 105.
C. 315.
D. 420.
Hệ số của \[{x^{12}}\]trong khai triển \[{\left( {{x^2} + x} \right)^{10}}\] là
A.\(C_{10}^6{.2^6}\).
B. \(C_{10}^6\).
C. \(C_{10}^8\).
D. \( - C_{10}^2\).
Cho hình chóp \(S.ABCD\). Gọi \(M\)và \(N\) lần lượt là trung điểm của \(SA\) và \(SC\). Khẳng định nào sau đây là đúng?
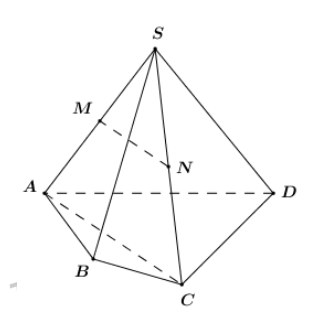
A.\(MN||mp\left( {ABCD} \right)\).
B. \(MN||mp\left( {SAB} \right)\).
C. \(MN||mp\left( {SBC} \right)\).
D. \(MN||mp\left( {SCD} \right)\).
Trong mặt phẳng tọa độ Oxy, cho \(\Delta :x - 2y - 1 = 0\) và \(\overrightarrow u \left( {4;3} \right)\). Gọi \(d\) là đường thẳng sao cho \({T_{\overrightarrow u }}\) biến \(d\) thành đường thẳng \(\Delta \). Phương trình đường thẳng \(d\) là
A.\(x - 2y + 1 = 0\).
B. \(x - 2y + 9 = 0\).
C. \(x - 2y - 3 = 0\).
D. \(x - 2y - 9 = 0\).
Cho hình vuông ABCD tâm O. Ảnh của đường thẳng CD qua phép quay tâm O, góc quay -90° là:
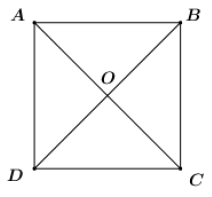
A. đường thẳng AB.
B. đường thẳng AC.
C. đường thẳng DA.
D. đường thẳng BC.
Trong không gian, mệnh đề nào sau đây đúng?
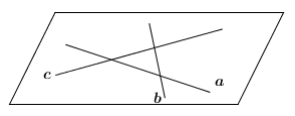
A. Nếu một đường thẳng cắt hai đường thẳng cắt nhau tại hai điểm phân biệt thì cả ba đường thẳng đó cùng nằm trên một mặt phẳng.
B. Nếu ba đường thẳng đồng quy thì chúng cùng nằm trên một mặt phẳng.
C. Nếu một đường thẳng cắt hai đường thẳng cho trước thì cả ba đường thẳng cùng nằm trong một mặt phẳng.
D. Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cũng cắt đường thẳng còn lại.
Cho hình chóp S.ABCD có ABCD là hình thang cân đáy lớn AD. Gọi M, N, P lần lượt là trung điểm của AB, CD, SB. Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng \(\left( {MNP} \right)\) là
A. hình bình hành.
B. hình thang.
C. hình chữ nhật.
D. hình vuông.
Nghiệm của phương trình \[\sqrt 3 \tan x - 1 = 0\] là
A.\[x = - \frac{\pi }{6} + k2\pi \left( {k \in \mathbb{Z}} \right)\].
B. \[x = \frac{\pi }{6} + k\pi \left( {k \in \mathbb{Z}} \right)\].
C. \[x = - \frac{\pi }{3} + k\pi \left( {k \in \mathbb{Z}} \right)\].
D. \[x = - \frac{\pi }{3} + k2\pi \left( {k \in \mathbb{Z}} \right)\].
Số nghiệm của phương trình \(2\cos x + 1 = 0\) thuộc khoảng \(\left( { - \pi ;4\pi } \right)\) là:
A. 4.
B. 2.
C. 3.
D. 5.
Cho số tự nhiên \(n\)thỏa mãn \(A_n^2 = 132\). Giá trị của \(n\)là:
A.\(n = 10\).
B. \(n = 12\).
C. \(n = 11\).
D. \(n = 13\).
Gieo ngẫu nhiên 3 con súc sắc cân đối, đồng chất. Xác suất để tích số chấm xuất hiện trên ba con súc sắc là một số tự nhiên chẵn là:
A.\(\frac{1}{8}\).
B. \(\frac{7}{8}\).
C.\(\frac{{23}}{{24}}\).
D.\(\frac{1}{2}\).
Mệnh đề nào dưới đây sai?
A. Hàm số \(y = \tan x\) là hàm số lẻ.
B. Hàm số \(y = \cos x\) là hàm số chẵn.
C. Hàm số \(y = \sin x\) là hàm số chẵn.
D. Hàm số \(y = \cot x\) là hàm số lẻ.
Hàm số \(y = \cos x\) đồng biến trên khoảng nào dưới đây?
A.\(\left( { - \pi ;\frac{{3\pi }}{4}} \right)\).
B. \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
C. \(\left( {0;\pi } \right)\).
D. \(\left( { - \pi ;0} \right)\).
Số các giá trị nguyên của tham số \(m\) để phương trình \(m\sin x + 3\cos x = 2m\) có nghiệm là:
A. 2.
B. 4.
C. 1.
D. 3.
Tập xác định của hàm số \(y = \frac{1}{{\sin x + \cos x}}\) là:
A.\(D = \mathbb{R}\backslash \left\{ { - \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}} \right\}\)
B.\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\)
C.\(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\)
D.\(D = \mathbb{R}\backslash \left\{ { - \frac{\pi }{4} + k2\pi ,k \in \mathbb{Z}} \right\}\)
Trong mặt phẳng tọa độ Oxy cho \(A\left( { - 2;3} \right)\) và \(I\left( {1;5} \right)\). Gọi \(B\) là ảnh của \(A\) qua phép đối xứng tâm \(I\). Tọa độ điểm \(B\) là
A.\(B\left( {0;13} \right)\).
B. \(B\left( {3;2} \right)\).
C. \(B\left( { - 5;1} \right)\).
D. \(B\left( {4;7} \right)\).
Từ các chữ số 0, 1, 2, 3, 4, 5, 6 lập được bao nhiêu số tự nhiên có 4 chữ số?
A. 2058
B. 2401
C. 720
D. 840
Nghiệm của phương trình \(\sin x + \sqrt 3 \cos x = 2\) là:
A.\(x = \frac{{5\pi }}{6} + k\pi ,{\rm{ }}k \in \mathbb{Z}\)
B. \(x = \frac{\pi }{6} + k2\pi ,{\rm{ }}k \in \mathbb{Z}\)
C. \(x = - \frac{\pi }{6} + k\pi ,{\rm{ }}k \in \mathbb{Z}\)
D. \(x = \frac{{5\pi }}{6} + k2\pi ,{\rm{ }}k \in \mathbb{Z}\)
Hệ số của \({x^5}\) trong khai triển \(P\left( x \right) = x{\left( {1 - 2x} \right)^5} + {x^2}{\left( {1 + 3x} \right)^{10}}\) là:
A. 3240
B. 80
C. 3320
D. 259200
Từ các số 1, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên chẵn có 4 chữ số đôi một khác nhau?
A. 49
B. 45
C. 47
D. 48
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải