50 CÂU HỎI
Cho hàm số \[f\left( x \right) = {x^3} + 3{x^2} - m\]. Tìm các giá trị của m để đồ thị hàm số \[f\left( x \right)\] cắt trục hoành tại 3 điểm phân biệt?
A. \[\left[ \begin{array}{l}m \le 0\\m \ge 4\end{array} \right.\].
B. \(m \in \left[ {0;4} \right]\).
C. \[\left[ \begin{array}{l}m < 0\\m > 4\end{array} \right.\].
D. \[m \in \left( {0;4} \right)\].
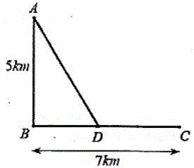
Một đoàn cứu trợ lũ lụt đang ở vị trí A của một tỉnh miền trung muốn đến xã C để tiếp tế lương thực và thuốc men. Để đi đến C, đoàn cứu trợ phải chèo thuyền từ A đến vị trí D với vận tốc 4 (km/h), rồi đi bộ đến C với vận tốc 6 (km/h). Biết A cách B một khoảng 5km, B cách C một khoảng 7km (hình vẽ). Hỏi vị trí điểm D cách A bao xa để đoàn cứu trợ đi đến xã C nhanh nhất?
A. \[AD = 5\sqrt 3 km\].
B. \(AD = 2\sqrt 5 km\).
C. \[5\sqrt 2 km\].
D. \[AD = 3\sqrt 5 km\].
Đồ thị hàm số \(y = \frac{{\sqrt {x - 3} }}{{{x^2} + x - 6}}\) có bao nhiêu đường tiệm cận?
A. 2.
B. 1.
C. 3.
D. 0.
Cho hàm số \[y = f\left( x \right)\] có đạo hàm liên tục trên R và đồ thị hàm số \[y = f'\left( x \right)\] như hình vẽ.
Khẳng định nào sau đây sai ?
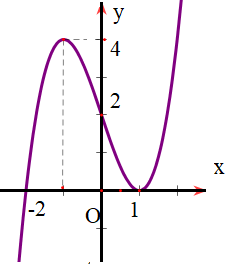
A. Hàm số y = f(x) đồng biến trên khoảng \(\left( {1; + \infty } \right)\)
B. Hàm số y = f(x) đồng biến trên khoảng \(\left( { - 2; - 1} \right)\)
C. Hàm số y = f(x) nghịch biến trên khoảng \(\left( { - 1;1} \right)\)
D. Hàm số y = f(x) nghịch biến trên khoảng \(\left( { - \infty ; - 2} \right)\)
Cho hàm số có đồ thị như hình vẽ sau. Hàm số đó là hàm số nào?
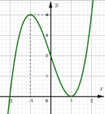
A. \(y = {x^3} - {x^2} + 1\).
B. \(y = {x^3} + {x^2} + 1\).
C. \(y = {x^3} - 3x + 2\).
D. \(y = - {x^3} + 3x + 2\)
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\), hàm số \(y = f'\left( x \right)\) có đồ thị hàm số như hình dưới
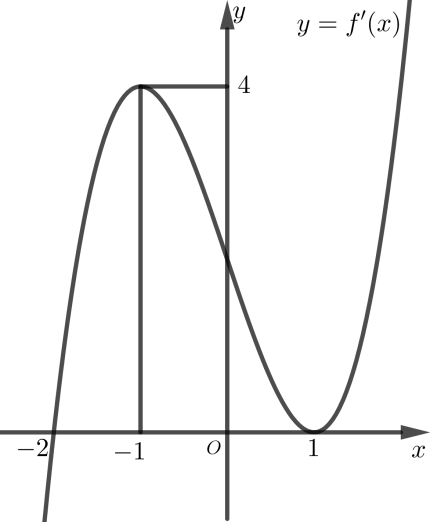
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào trong các khoảng sau:
A. \(\left( { - \infty ;2} \right);\left( {1; + \infty } \right)\)
B. \(\left( { - 2; + \infty } \right){\rm{\backslash }}\left\{ 1 \right\}\)
C. \(\left( { - 2; + \infty } \right)\)
D. \(\left( { - 4;0} \right)\)
Trong một khối đa diện, mệnh đề nào sau đây đúng?
A. Hai cạnh bất kì có ít nhất một điểm chung.
B. Ba mặt bất kì có ít nhất 1 đỉnh chung.
C. Hai mặt bất kì có ít nhất một điểm chung.
D. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
Cho hàm số \(y = \frac{{8x - 5}}{{x + 3}}\). Kết luận nào sau đây đúng?
A. Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 3} \right) \cup \left( { - 3; + \infty } \right)\).
B. Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\).
C. Hàm số luôn đồng biến trên \(\mathbb{R}\).
D. Hàm số đồng biến trên từng khoảng xác định của nó.
Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây?

A. \[y = - {x^3} - 3x - 2\].
B. \[y = {x^3} - 3{x^2} - 1\].
C. \[y = - {x^3} + 3{x^2} - 2\].
D. \[y = - {x^3} + 3{x^2} - 1\].
Tìm tất cả các giá trị của tham số \(m\) để phương trình \(x - m - \sqrt {9 - {x^2}} = 0\) có đúng 1 nghiệm dương?
A. \(m \in \left( { - 3;3} \right]\).
B. \(m \in \left( { - 3;3} \right] \cup \left\{ { - 3\sqrt 2 } \right\}\).
C. \(m \in \left[ {0;3} \right]\).
D. \(m = \pm 3\sqrt 2 \).
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình bên. Trong các mệnh đề sau mệnh đề nào đúng ?
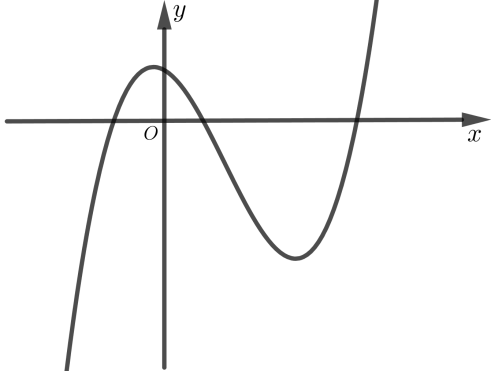
A. \(ab < 0,bc > 0,cd < 0\)
B. \(ab < 0,bc < 0,cd > 0\)
C. \(ab > 0,bc > 0,cd < 0\)
D. \(ab > 0,bc > 0,cd > 0\)
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(R\) và có bảng biến thiên như sau. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
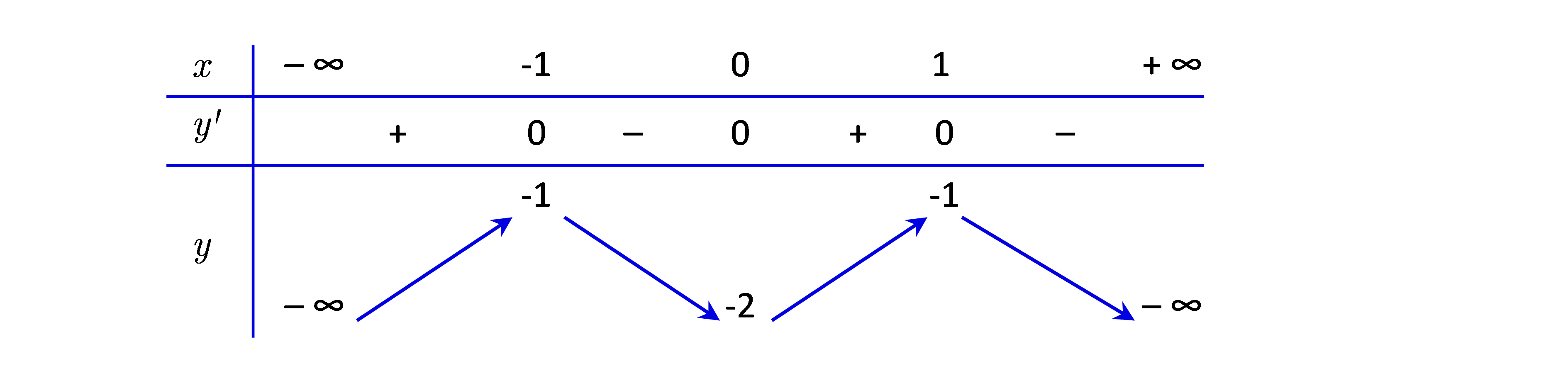
A. \[\left( {0;1} \right)\].
B. \(\left( { - 1;0} \right)\).
C. \[\left( { - \infty ;1} \right)\].
D. \[\left( {1; + \infty } \right)\].
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
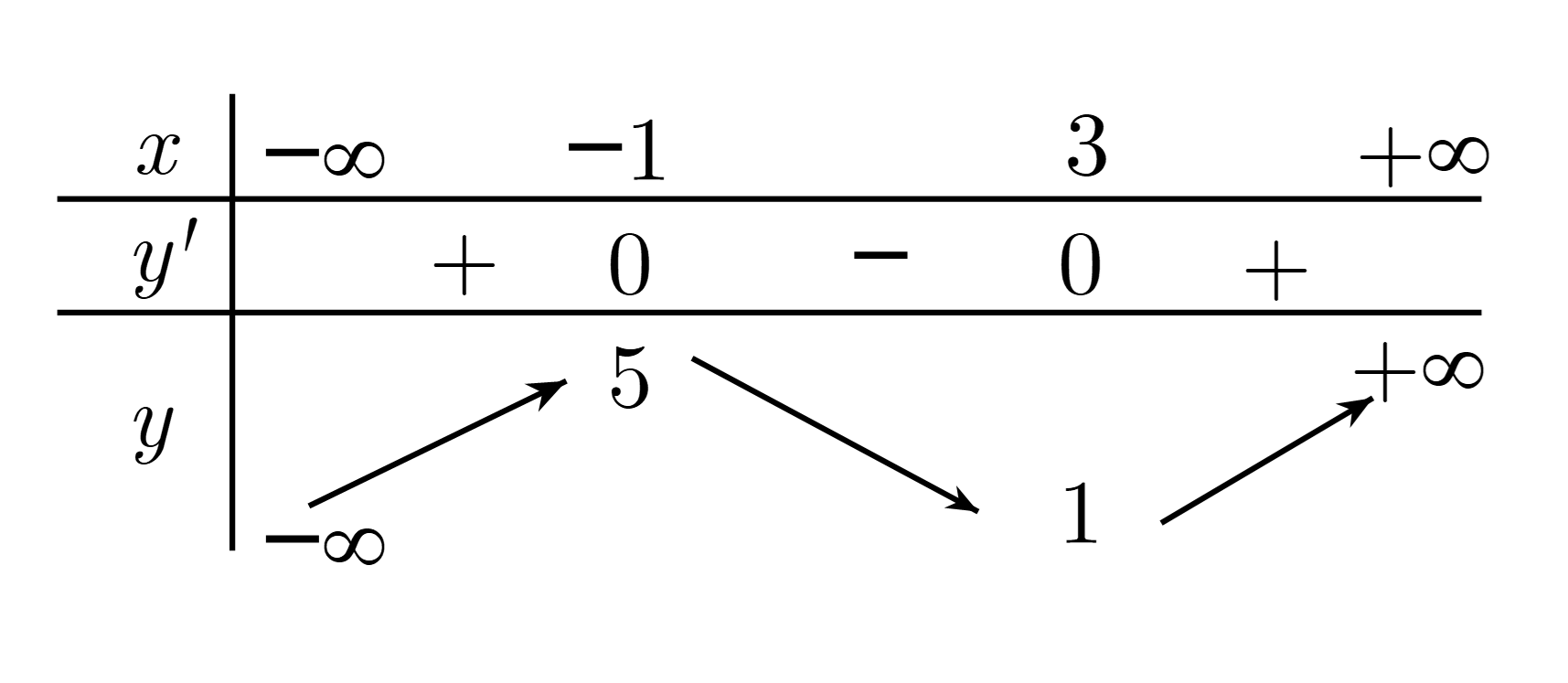
Đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) có bao nhiêu điểm cực trị?
A. \(2\).
B. \(3\).
C. \(4\).
D. \(5\).
Cho đồ thị \(\left( C \right)\) của hàm số \(y = {x^3} - 3x + 2\). Số các tiếp tuyến với đồ thị \(\left( C \right)\) mà các tiếp tuyến đó vuông góc với đường thẳng \(d:y = - \frac{1}{3}x + 1\) là:
A. \(1\).
B. \(2\).
C. \(3\).
D. \(0\).
Giá trị nhỏ nhất của hàm số \[y = 3\cos 2x - 4\sin x\] là
A. \(1\).
B. \( - 7\).
C. \( - 5\)
D. \(\frac{{11}}{3}\).
Cho hàm \[y = f(x)\] liên tục trên đoạn \[\left[ { - 2;\,2} \right]\] và có đồ thị như hình vẽ bên.
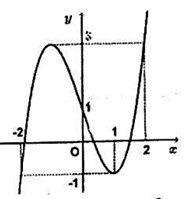
Số nghiệm của phương trình \[3f(x + 2) - 4 = 0\] trên đoạn \[\left[ { - 2;\,2} \right]\] là ?
A. \[4\].
B. \[2\].
C. \[3\].
D. \[1\].
Cho hàm số có đồ thị như hình vẽ dưới đây. Chọn kết luận sai trong các kết luận sau:
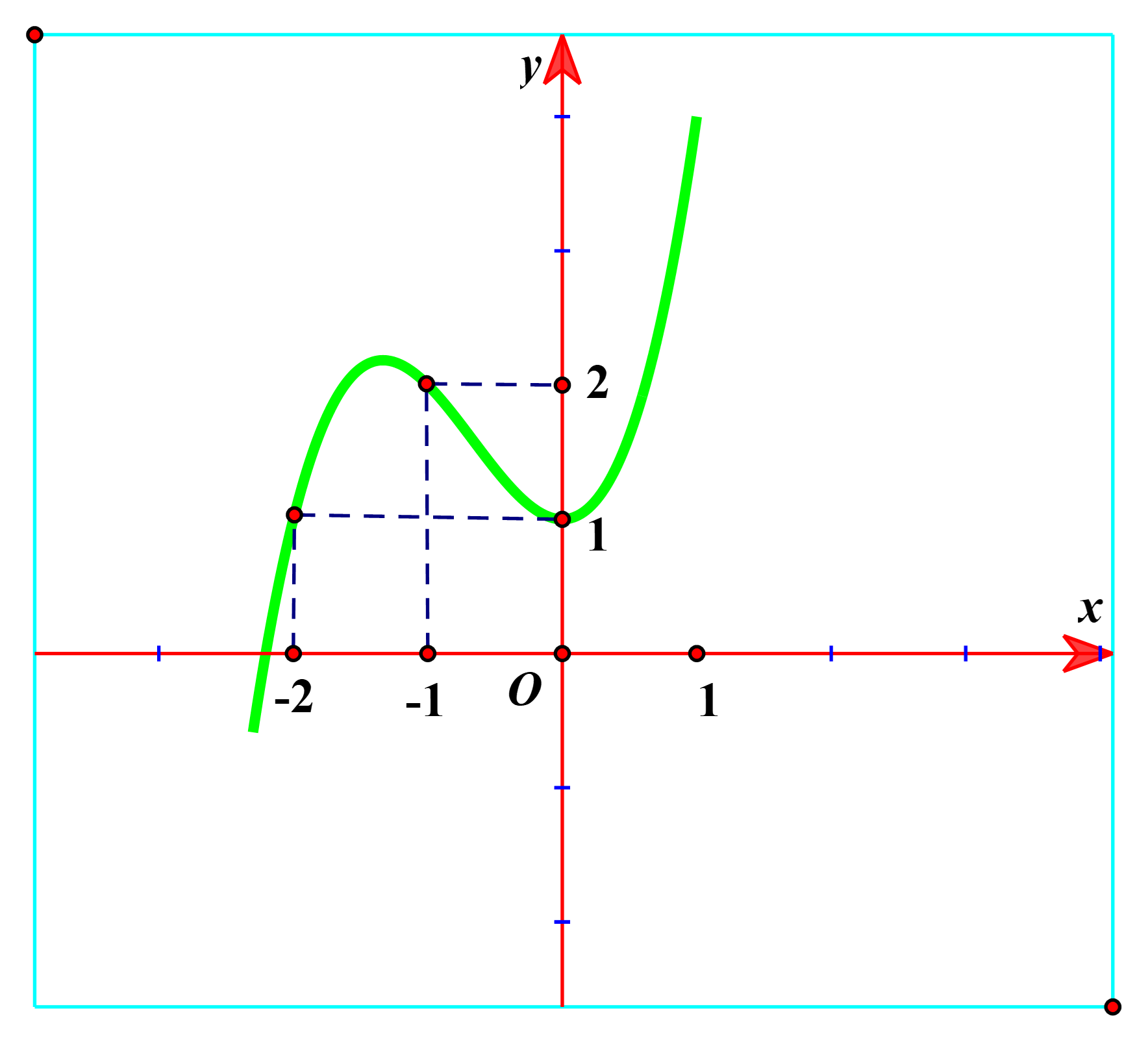
A. Hàm số đạt cực tiểu tại \(x = 0.\)
B. Đồ thị hàm số cắt trục \(Oy\)tại điểm \(\left( {0;1} \right).\)
C. Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right).\)
D. Hàm số nghịch biến trên khoảng \(\left( { - 2; - 1} \right).\)
Hàm số \[y = {x^3} - \left( {m + 2} \right)x + m\] đạt cực tiểu tại \[x = 1\] khi:
A. \[m = - 1\].
B. \[m = 2\].
C. \[m = - 2\].
D. \[m = 1\].
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \[a\], mặt bên \[SAB\] là tam giác cân tại \[S\] và nằm trong mặt phẳng vuông góc với đáy; góc giữa đường thẳng \[SC\] và mặt phẳng đáy bằng \[{45^0}\]. Thể tích khối chóp \[S.ABCD\] bằng
A. \[\frac{{{a^3}\sqrt 3 }}{{12}}\].
B. \[\frac{{{a^3}\sqrt 3 }}{9}\].
C. \[\frac{{{a^3}\sqrt 5 }}{{24}}\].
D. \[\frac{{{a^3}\sqrt 5 }}{6}\].
Cho lăng trụ đứng ABC. A’B’C’ có đáy ABC là tam giác vuông tại A với \(AC = a\sqrt 3 \) . Biết BC’ hợp với mặt phẳng (AA’C’C) một góc 300 và hợp với mặt phẳng đáy góc \(\alpha \) sao cho \(\sin \alpha = \frac{{\sqrt 6 }}{4}\) . Gọi M, N lần lượt là trung điểm cạnh BB’ và A’C’. Khoảng cách MN và AC’ là :
A. \(\frac{{a\sqrt 6 }}{4}\)
B. \(\frac{{a\sqrt 3 }}{6}\)
C. \(\frac{{a\sqrt 5 }}{4}\)
D. \(\frac{a}{3}\)
Cho hàm số \[y = {x^3} - 3{x^2} - 9x + 2\]. Chọn kết luận đúng:
A. Hàm số đạt cực tiểu tại \[x = 3\].
B. Hàm số đạt cực tiểu tại \[x = - 1\].
C. Hàm số đat cực tại tại \[x = 1\].
D. Hàm số đạt cực đại tại \[x = 3\].
Với giá trị nào của tham số để đồ thị hàm số ![]() có tiệm cận ngang.
có tiệm cận ngang.
A. \[m = 1\].
B. m = -1.
C. ![]() .
.
D. Không có m.
Số giao điểm của đường cong \(y = {x^3} - 2{x^2} + 2x + 1\) và đường thẳng \(y = 1 - x\) là
A. \[1\].
B. \(2\).
C. \[3\].
D. \[0\].
Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) như hình vẽ
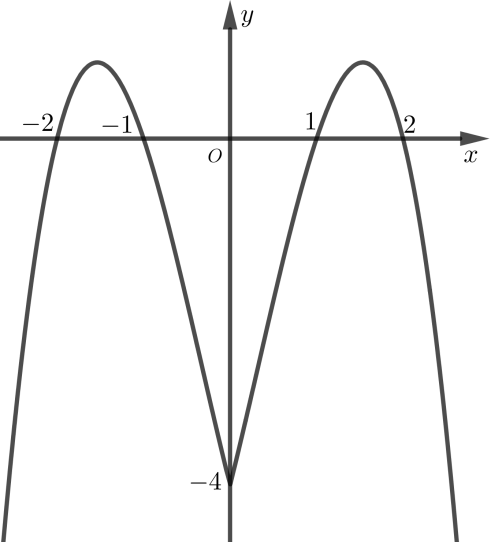
Chọn kết luận đúng trong các kết luận sau:
A. \(f\left( x \right) = - {x^3} + {x^2} + 4x - 4\)
B. \(f\left( x \right) = {x^3} - {x^2} - 4x + 4\)
C. \(f\left( x \right) = - {x^3} - {x^2} + 4x + 4\)
D. \(f\left( x \right) = {x^3} + {x^2} - 4x - 4\)
Cho hàm số \(y = - {x^3} - m{x^2} + \left( {4m + 9} \right)x + 5\) (với m là tham số). Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng \(\left( { - \infty ; + \infty } \right)\)?
A. 7
B. 6
C. 5
D. 8
Cho hình chóp \[S.ABCD\]có \[ABCD\] là hình thang vuông tại \[A\] và \[D\], \[AB = AD = a\],\[CD = 2a\]. Hình chiếu của \[S\]lên mặt phẳng \[(ABCD)\]trùng với trung điểm của \[BD\]. Biết thể tích tứ diện \[SBCD\] bằng \(\frac{{{a^3}}}{{\sqrt 6 }}\). Tính khoảng cách từ \[A\]đến mặt phẳng \[(SBC)\] là:
A. \(\frac{{a\sqrt 3 }}{2}\).
B. \(\frac{{a\sqrt 2 }}{6}\).
C. \(\frac{{a\sqrt 3 }}{6}\).
D. \(\frac{{a\sqrt 6 }}{4}\).
Một khối lập phương có cạnh bằng \(a\,\,\left( {{\rm{cm}}} \right)\). Khi tăng kích thước của mỗi cạnh thêm \(2\,\,\left( {{\rm{cm}}} \right)\) thì thể tích tăng thêm \(98\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\). Giá trị \(a\) bằng:
A. \(6\,\,\left( {{\rm{cm}}} \right)\)
B. \(5\,\,\left( {{\rm{cm}}} \right)\)
C. \(4\,\,\left( {{\rm{cm}}} \right)\).
D. \(3\,\,\left( {{\rm{cm}}} \right)\).
Hàm đồ thị \((C):y = {x^3} - 3{x^2}.\) Có bao nhiêu số nguyên \(b \in ( - 10;10)\) để có đúng một tiếp tuyến của \((C)\) qua \((0;b)\)
A. \(9\).
B. \(16\).
C. \(2\) .
D. \(17\).
Cho hình chóp \[S.ABCDE\] có đáy là hình ngũ giác và có thể tích là \[V\]. Nếu tăng chiều cao của hình chóp lên \[3\] lần đồng thời giảm độ dài các cạnh đi \[3\]lần thì ta được khối chóp mới \[S'.A'B'C'D'E'\] có thể tích là \[V'\]. Tỉ số thể tích \[\frac{{V'}}{V}\] là:
A. \[3\].
B. \(\frac{1}{5}\).
C. \[1\].
D. \[\frac{1}{3}\].
Cho hình lăng trụ \(ABCD.A'B'C'D'\) có đáy \(ABCD\)là hình thoi cạnh a,\[\widehat {ABC} = {60^0}\] . Chân đường cao hạ từ B’ trùng với tâm O của đáy \(ABCD\); góc giữa mặt phẳng \(\left( {BB'C'C} \right)\) với đáy bằng \({60^0}\). Thể tích lăng trụ bằng:
A. \(\frac{{3{a^3}\sqrt 3 }}{8}\)
B. \(\frac{{2{a^3}\sqrt 3 }}{9}\)
C. \(\frac{{3{a^3}\sqrt 2 }}{8}\)
D. \(\frac{{3{a^3}}}{4}\)
Số đường tiệm cận của đồ thị hàm số \[y = \frac{{2 - x}}{{1 + \left| x \right|}}\] là:
A. \[2\].
B. \(0\).
C. \[3\].
D. \[1\].
Cho hàm số \(f\left( x \right) = \frac{{\sin x - m}}{{\sin x + 1}}\). Tìm giá trị của tham số \(m\) để giá trị lớn nhất của hàm số trên đoạn \(\left[ {0;\frac{{2\pi }}{3}} \right]\) bằng \( - 2\)?
A. \(m = 5.\)
B. \(\left[ {\begin{array}{*{20}{c}}{m = 5}\\{m = 2}\end{array}} \right..\)
C. \(m = 2.\)
D. \(m = 3.\)
Hình bát diện đều có bao nhiêu đỉnh?
A. 10.
B. 8.
C. 6.
D. 12.
Cho hàm số\[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\] và có đồ thị hàm số \[y = f'\left( x \right)\] như hình bên.
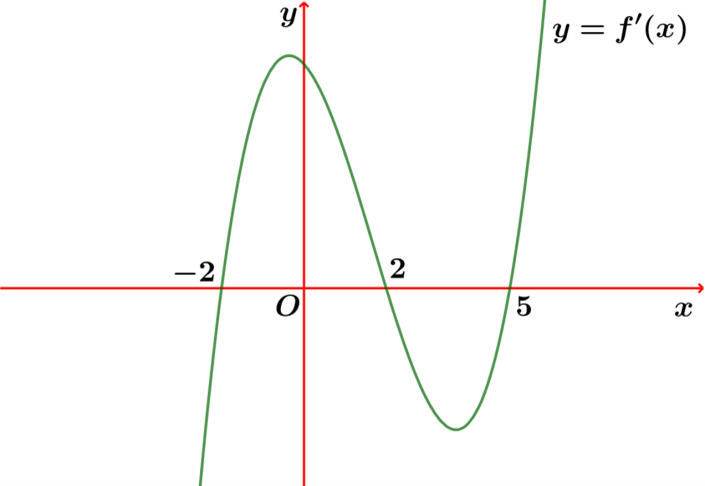
Hỏi hàm số \[g\left( x \right) = f\left( {3 - 2x} \right)\] nghịch biến trên khoảng nào sau đây?
A. \[\left( { - 1; + \infty } \right)\]
B. \[\left( { - \infty ; - 1} \right)\]
C. \[\left( {1;3} \right)\]
D. \[\left( {0;2} \right)\]
Hình lăng trụ có thể có số cạnh là số nào sau đây?
A. \(2017\)
B. \(2019\)
C. \(2018\)
D. \(2020\)
Một xưởng sản xuất cần làm \(100\) chiếc hộp inox bằng nhau, hình dạng là hình hộp chữ nhật có đáy là hình vuông (hộp không có nắp), với thể tích là \(108d{m^3}\)/1 hộp. Giá inox là \(47.000\) đồng/ \(1d{m^2}\). Hãy tính toán sao cho tổng tiền chi phí cho \(100\) chiếc hộp là ít nhất, và số tiền tối thiểu đó là bao nhiêu (nếu chỉ tính số inox vừa đủ để sản xuất \(100\) chiếc hộp, không có phần dư thừa, cắt bỏ)?
A. \(1.692.000.000\)đồng.
B. \(507.666.000\)đồng.
C. \(1.015.200.000\)đồng.
D. \(253.800.000\)đồng.
Phương trình tiếp tuyến với đồ thị (C) của hàm số: \[y = {x^3} - 3x + 1\], biết tiếp tuyến song song với đường thẳng \[\left( d \right):y = 9x + 17\]là:
A. \(\left[ \begin{array}{l}y = 9x + 19\\y = 9x - 21\end{array} \right.\).
B. \(\left[ \begin{array}{l}y = 9x - 19\\y = 9x + 21\end{array} \right.\).
C. \(\left[ \begin{array}{l}y = 9x - 15\\y = 9x + 17\end{array} \right.\).
D. \(y = 9x - 15\).
Giá trị lớn nhất của hàm số \[f\left( x \right) = 2{x^3} + 3{x^2} - 12x + 2\] trên đoạn \[\left[ { - 1;2} \right]\] là
A. \[11\].
B. \(10\).
C. \[6\].
D. \[15\].
Khẳng định nào sau đây sai?
A. Hai khối lập phương lần lượt có cạnh là \[4cm\] và \[8cm\] là hai khối đa diện đồng dạng.
B. Khối chóp tam giác đều là khối chóp có đáy là tam giác đều.
C. Hai khối tứ diện đều có diện tích mỗi mặt là \[3{m^2}\] và \[12{m^2}\] là hai khối đa diện đều.
D. Khối lăng trụ tứ giác đều và khối hộp chữ nhật là hai khối đa diện đồng dạng.
Trung điểm các cạnh của hình tứ diện đều là đỉnh của hình:
A. Hình lập phương.
B. Hình tứ diện đều.
C. Hình lăng trụ tam giác.
D. Hình bát diện đều.
Cho hàm số \(y = x - \sin 2x + 3\). Chọn kết luận đúng.
A. Hàm số đạt cực tiểu tại \(x = \frac{\pi }{3}\).
B. Hàm số đạt cực tiểu tại \(x = \frac{{ - \pi }}{6}\) .
C. Hàm số đạt cực đại tại \(x = \frac{\pi }{6}\) .
D. Hàm số đạt cực đại tại \(x = \frac{{ - \pi }}{6}\).
Đường thẳng \[y = 2\] là tiệm cận ngang của hàm số nào sau đây ?
A. \[y = \frac{{2{x^2} + 1}}{{2 - x}}\]
B. \[y = \frac{{{x^2} + 2x + 1}}{{1 + x}}\]
C. \[y = \frac{{x + 1}}{{1 - 2x}}\]
D. \[y = \frac{{2x - 2}}{{x + 2}}\]
Hình đa diện có bao nhiêu cạnh?
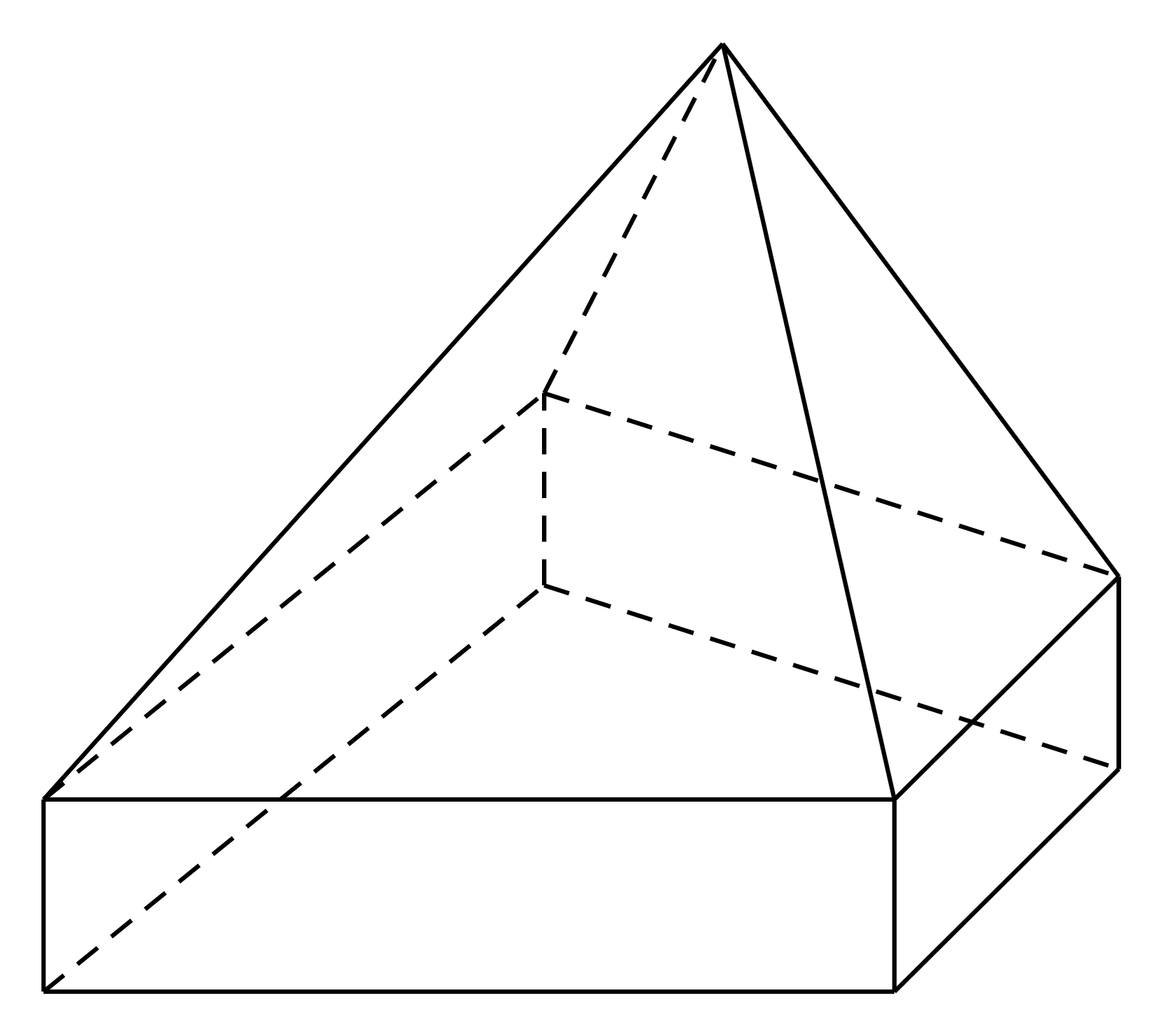
A. 15.
B. 12.
C. 20.
D. 16.
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
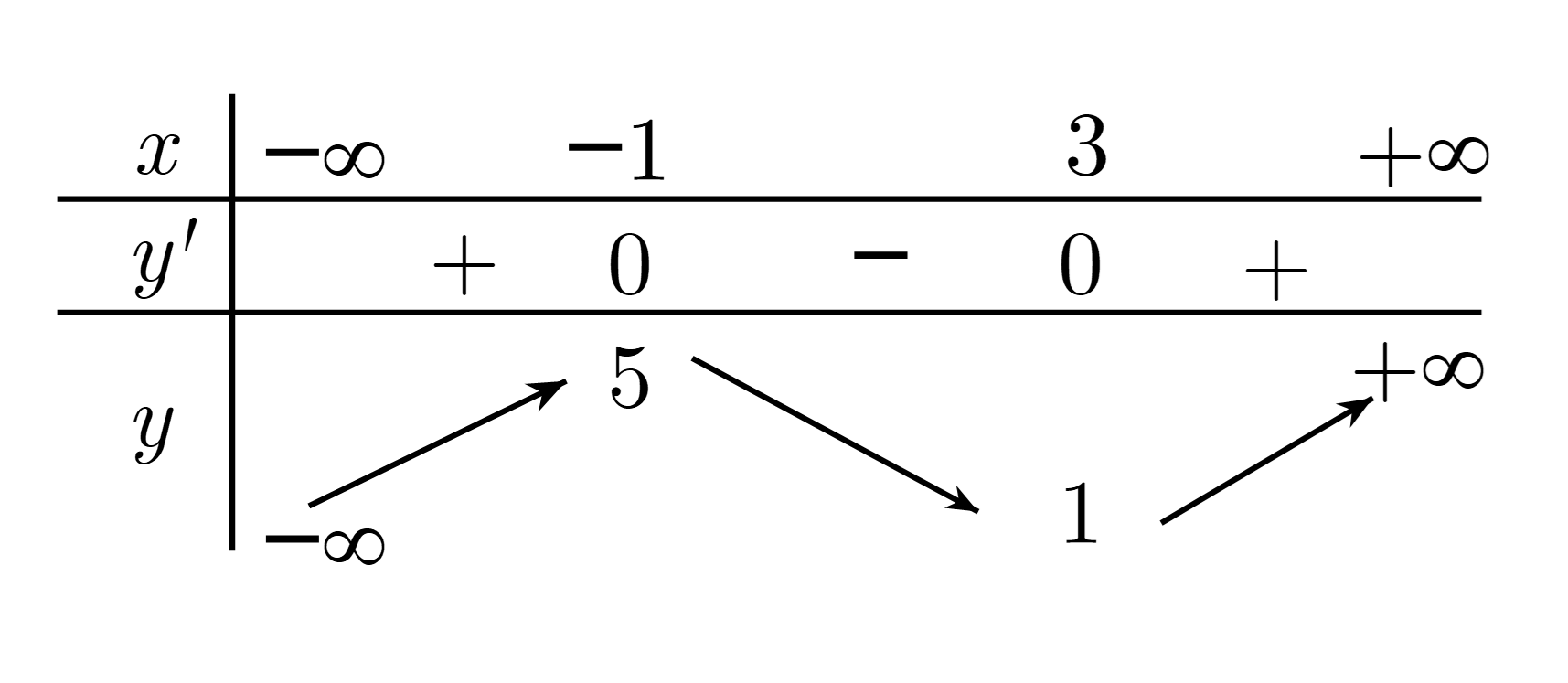
Đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) có bao nhiêu điểm cực trị?
A. \(2\).
B. \(3\).
C. \(4\).
D. \(5\).
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
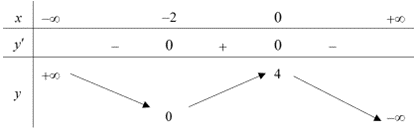
Khẳng định nào sau đây sai ?
A. Hàm số đồng biến trên \(\left( { - 2\,;\,0} \right)\).
B. Hàm số đạt giá trị lớn nhất là \(4\).
C. Đường thẳng \(y = 2\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại \(3\) điểm phân biệt.
D. Hàm số đạt cực tiểu tại \(x = - 2\).
Cho hàm số \[y = \frac{{x - 1}}{{x + 1}}\]. Phương trình tiếp tuyến của đồ thị hàm số tại điểm \[M\left( {1;0} \right)\] là:
A. \[y = \frac{1}{2}x - \frac{3}{2}\].
B. \[y = \frac{1}{2}x - \frac{1}{2}\].
C. \[y = \frac{1}{2}x + \frac{1}{2}\].
D. \[y = \frac{1}{4}x - \frac{1}{2}\].
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác vuông cân tại \(B\),\(AB = a\) và \(A'B = a\sqrt 3 \). Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng:
A. \(\frac{{{a^3}\sqrt 3 }}{2}\)
B. \(\frac{{{a^3}}}{6}\)
C. \(\frac{{{a^3}}}{2}\)
D. \(\frac{{{a^3}\sqrt 2 }}{2}\)
Số mặt phẳng đối xứng của hình lập phương là
A. \[3.\]
B. \(6.\)
C. \[8.\]
D. \[9.\]
Cho hình chóp tứ giác đều \[S.ABCD\]có thể tích \[V\], có \[O\] là tâm của đáy. Lấy \[M\] là trung điểm của cạnh bên\[SC\] . Thể tích khối tứ diện \[ABMO\]bằng
A. \[\frac{V}{4}.\]
B. \(\frac{V}{2}.\)
C. \[\frac{V}{{16}}.\]
D. \[\frac{V}{8}.\]
Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh \(a\), cạnh bên \(SC\) vuông góc với mặt phẳng \((ABC)\), \(SC = a\). Thể tích của khối chóp \(S.ABC\)bằng
A. \(\frac{{{a^3}\sqrt 3 }}{3}\)
B. \(\frac{{{a^3}\sqrt 2 }}{{12}}\)
C. \(\frac{{{a^3}\sqrt 3 }}{9}\)
D. \(\frac{{{a^3}\sqrt 3 }}{{12}}\)

