Quiz

Bộ 20 đề thi giữa học kì 1 Toán 12 năm 2022-2023 có đáp án- Đề 21

Admin50 câu hỏiToánLớp 12

Bắt đầu ngay

50 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Có bao nhiêu loại khối đa diện đều mà mỗi mặt của nó là một tam giác đều?

A. 3

B. 1

C. 5

D. 2

2. Nhiều lựa chọn

Cho hàm số $y = x^{4} - 2 x^{2} - 5$ . Kết luận nào sau đây đúng?

A. Hàm số đồng biến trên khoảng $(- \infty; - 1)$ .

B. Hàm số nghịch biến với mọi x.

C. Hàm số đồng biến với mọi x.

D. Hàm số đồng biến trên khoảng $(- 1; 0)$ và $(1; + \infty)$ .

3. Nhiều lựa chọn

Cho hàm số f(x) có đạo hàm cấp 2 trên khoảng K và $x_{0} \in K .$ Tìm mệnh đề sai trong các mệnh đề sau:

A. Nếu hàm số đạt cực đại tại $x_{0}$ thì ${f^{'}}^{'} (x_{0}) < 0$ .

B. Nếu hàm số đạt cực đại tại $x_{0}$ thì tồn tại $a < x_{0}$ để $f^{'} (a) > 0$ .

C. Nếu hàm số đạt cực trị tại $x_{0}$ thì $f^{'} (x_{0}) = 0$ .

D. Nếu $f^{'} (x_{0}) = 0$ và ${f^{'}}^{'} (x_{0}) \neq 0$ thì hàm số đạt cực trị tại $x_{0}$ .

4. Nhiều lựa chọn

Cho khối tự diện OABC có OA , OB, OC đôi một vuông góc và OA=a; OB=b; OC=c. Thể tích khối tứ diện OABC được tính theo công thức nào sau đây

A. $V = \frac{1}{2} a . b . c$

B. $V = \frac{1}{3} a . b . c$

C. $V = \frac{1}{6} a . b . c$

D. $V = 3 a . b . c$

5. Nhiều lựa chọn

Tính diện tích toàn phần của hình lập phương có độ dài đường chéo bằng $\sqrt{12}$ .

A. 18

B. 24

C. 12

D. 16

6. Nhiều lựa chọn

Bảng biến thiên trong hình vẽ là của hàm số

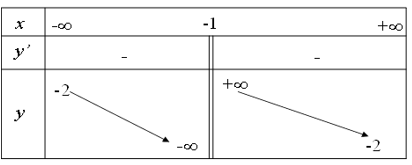
Bảng biến thiên trong hình vẽ là của hàm số (ảnh 1)

A. $y = \frac{x - 4}{2 x + 2}$

B. $y = \frac{- 2 x - 4}{x + 1}$

C. $y = \frac{- 2 x + 3}{x + 1}$

D. $y = \frac{2 - x}{x + 1}$

7. Nhiều lựa chọn

Cho hình lăng trụ tam giác đều ABCA'B'C' có AB= 2a, $A A^{'} = a \sqrt{3}$ . Tính thể tích khối lăng trụ ABCA'B'C'.

A. $\frac{3 a^{3}}{4}$

B. $\frac{a^{3}}{4}$

C. $3 a^{3}$

D. $a^{3}$

8. Nhiều lựa chọn

Cho hàm số y=f(x) liên tục trên R và có bảng xét dấu f'(x)như sau:

Cho hàm số y=f(x) liên tục trên R và có bảng xét dấu f'(x)như sau: Hàm số y=f(x) có bao nhiêu điểm cực trị? (ảnh 1)

Hàm số y=f(x) có bao nhiêu điểm cực trị?

A. 1

B. 2

C. 3

D. 4

9. Nhiều lựa chọn

Trong các hình dưới đây hình nào không phải đa diện lồi?

Trong các hình dưới đây hình nào không phải đa diện lồi? A. Hình (IV). (ảnh 1)

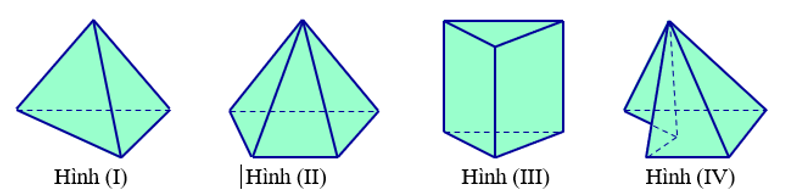
A. Hình (IV)

B. Hình (III).

C. Hình (II).

D. Hình (I).

10. Nhiều lựa chọn

Hàm số $y = x^{3} - 3 x$ nghịch biến trên khoảng nào?

A. $(- \infty; - 1)$

B. $(- \infty; + \infty)$

C. $(- 1; 1)$

D. $(0; + \infty)$

11. Nhiều lựa chọn

Khối lăng trụ có diện tích đáy bằng 3 $a^{2}$ , chiều cao bằng a có thể tích bằng

A. $3 a^{3}$

B. $\frac{3}{2} a^{3}$

C. $\frac{1}{2} a^{3}$

D. $a^{3}$

12. Nhiều lựa chọn

Giá trị lớn nhất của hàm số $f (x) = \frac{- x^{2} - 4}{x}$ trên đoạn $[\frac{3}{2}; 4]$ là

A. -2

B. -4

C. $- \frac{25}{6}$

D. -5

13. Nhiều lựa chọn

Giá trị lớn nhất của hàm số $y = \frac{x + 1}{\sqrt{x^{2} + 1}}$ trên khoảng $(- \infty; + \infty)$ bằng

A. $2 \sqrt{2}$

B. 1

C. $\sqrt{2}$

D. 2

14. Nhiều lựa chọn

Một hồ bơi hình hộp chữ nhật có đáy là hình vuông cạnh bằng 50(m). Lượng nước trong hồ cao 1,5(m). Thể tích nước trong hồ là

A. $1875 (m^{3})$

B. $2500 (m^{3})$

C. $1250 (m^{3})$

D. $3750 (m^{3})$

15. Nhiều lựa chọn

Đồ thị hàm số nào trong bốn hàm số liệt kê ở bốn phương án A, B, C, D dưới đây, có đúng một điểm cực trị?

A. $y = x^{3} - 3 x^{2} + x$

B. $y = x^{4} + 2 x^{2} - 3$

C. $y = - x^{3} - 4 x + 5$

D. $y = \frac{2 x - 3}{x + 1}$

16. Nhiều lựa chọn

Tọa độ điểm M thuộc đồ thị hàm số $y = \frac{3 x + 1}{x - 1}$ cách đường tiệm cận đứng của đồ thị hàm số một khoảng bằng 1 là

A. $(0; - 1); (- 2; 7)$

B. $(- 1; 0); (2; 7)$

C. $(0; 1); (2; - 7)$

D. $(0; - 1); (2; 7)$

17. Nhiều lựa chọn

Hàm số $y = x^{2} - 4 x + 3$ có điểm cực tiểu là

A. $x = 4$

B. x=0

C. y=-1

D. x=2

18. Nhiều lựa chọn

Gọi I là giao điểm của hai đường tiệm cận của đồ thị hàm số $y = \frac{2 x - 3}{x + 1}$ . Khi đó, điểm I nằm trên đường thẳng có phương trình:

A. $x + y + 4 = 0$

B. $2 x - y + 4 = 0$

C. $x - y + 4 = 0$

D. $2 x - y + 2 = 0$

19. Nhiều lựa chọn

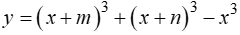Hàm số Hàm số y= ( x+3) 63+ ( x+n)^3-x^3 ( tham số m , n ) đồng biến trên khoảng ( - vô cùng, + vô cùng). Giá trị nhỏ nhất của biểu thức (ảnh 1) ( tham số m, n) đồng biến trên khoảng $(- \infty; + \infty)$ . Giá trị nhỏ nhất của biểu thức $P = 4 (m^{2} + n^{2}) - m - n$ bằng

A. $- \frac{1}{16}$

B. -16

C. 4

D. $\frac{1}{4}$

20. Nhiều lựa chọn

Cho hàm số $y = f (x)$ có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?

Cho hàm số có đồ thị như hình bên. Mệnh đề nào dưới đây đúng? A. Hàm số có giá trị cực tiểu bằng 2. (ảnh 1)

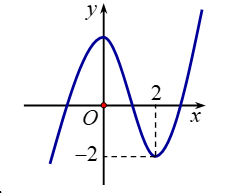
A. Hàm số có giá trị cực tiểu bằng 2.

B. Hàm số đạt cực đại tại $x = 0$ và đạt cực tiểu tại $x = 2$ .

C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -2.

D. Hàm số có ba điểm cực trị.

21. Nhiều lựa chọn

Cho hàm số y=f(x) xác định, liên tục trên R có bảng biến thiên như hình vẽ

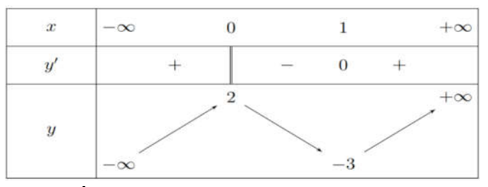
Cho hàm số y=f(x) xác định, liên tục trên R có bảng biến thiên như hình vẽ Hàm số đã cho nghịch biến trên khoảng nào sau đây? (ảnh 1)

Hàm số đã cho nghịch biến trên khoảng nào sau đây?

A. $(- 3; 2)$

B. $(- \infty; 0) v à (1; + \infty)$

C. $(- \infty; - 3)$

D. $(0; 1)$

22. Nhiều lựa chọn

Cho đồ thị hàm y=f(x) như hình vẽ. Số điểm cực trị của đồ thị hàm số là:

Cho đồ thị hàm y=f(x) như hình vẽ. Số điểm cực trị của đồ thị hàm số là: (ảnh 1)

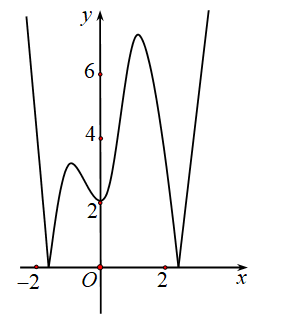
A. 4

B. 3

C. 5

D. 2

23. Nhiều lựa chọn

Cho hình trụ có bán kính đáy bằng R, chiều cao bằng h . Biết rằng hình trụ đó có diện tích toàn phần gấp đôi diện tích xung quanh. Mệnh đề nào sau đây đúng?

A. $R = h$

B. $R = 2 h$

C. $h = 2 R$

D. $h = \sqrt{2} R$

24. Nhiều lựa chọn

Tìm tất cả các giá trị thực của tham số m để hàm số $y = \frac{m x - 1}{m - 4 x}$ nghịch biến trên khoảng $(- \infty; \frac{1}{4})$ .

A. $m > 2$

B. $- 2 < m < 2$

C. $- 2 \leq m \leq 2$

D. $1 \leq m < 2$

25. Nhiều lựa chọn

Cho tứ diện ABCD Gọi B', C' lần lượt là trung điểm của AB, AC Khi đó tỉ số thể tích của khối tứ diện AB'C'D và khối tứ diện ABCD bằng:

A. $\frac{1}{8}$

B. $\frac{1}{2}$

C. $\frac{1}{4}$

D. $\frac{1}{6}$

26. Nhiều lựa chọn

Cho hàm số f(x) có đạo hàm $f^{'} (x) = {(x + 1)}^{2} {(x - 1)}^{3} (2 - x)$ . Hỏi hàm số đồng biến trên khoảng nào dưới đây?

A. $(2; + \infty)$

B. $(1; 2)$

C. $(- \infty; - 1)$

D. $(- 1; 1)$

27. Nhiều lựa chọn

Cho hàm số y=f(x) xác định trên $ℝ \ \{- 1\}$ , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình sau

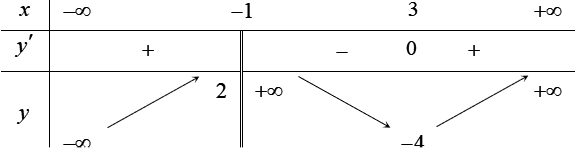
$Cho hàm số y=f(x) xác định trên R\ {-1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình sau (ảnh 1)$

Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình f(x)=m có đúng ba nghiệm thực phân biệt

A. $(- 4; 2)$

B. $[- 4; 2)$

C. $(- 4; 2]$

D. $(- \infty; 2]$

28. Nhiều lựa chọn

Giá trị nhỏ nhất của hàm số $y = \frac{x^{2} + 3}{x + 1}$ trên đoạn $[- 4; - 2]$ là

A. $\min_{[- 4; - 2]} y = - 7$

B. $\min_{[- 4; - 2]} y = - \frac{19}{3}$

C. $\min_{[- 4; - 2]} y = - 8$

D. $\min_{[- 4; - 2]} y = - 6$

29. Nhiều lựa chọn

Cho lăng trụ đứng ABCA'B'C'có đáy ABC là tam giác vuông tại A và AB=a $, A C = a \sqrt{3}$ mặt phẳng ( A'BC) tạo với mặt phẳng đáy ( ABC)một góc 30 $°$ . Tính thể tích khối lăng trụ ABCA'B'C'.

A. $\frac{a^{3}}{4}$

B. $\frac{a^{3} \sqrt{3}}{4}$

C. $\frac{a^{3}}{2}$

D. $\frac{a^{3} \sqrt{3}}{2}$

30. Nhiều lựa chọn

Tìm tất cả các giá trị của tham số m để hàm số $f (x) = x^{4} + x^{3} - m x^{2}$ có 3 điểm cực trị?

A. $m \in (0; + \infty)$

B. $m \in (- \frac{9}{2}; + \infty) \ \{0\}$

C. $m \in (- \infty; 0)$

D. $m \in (- \frac{9}{32}; + \infty) \ \{0\}$

31. Nhiều lựa chọn

Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng?

A. 6 mặt phẳng.

B. 3 mặt phẳng.

C. 9 mặt phẳng.

D. 4 mặt phẳng.

32. Nhiều lựa chọn

Một vật chuyển động theo quy luật $s = \frac{1}{3} t^{3} - t^{2} + 9 t,$ với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?

A. 89 $(m/s)$

B. 109 $(m/s)$

C. 71 $(m/s)$

D. $\frac{25}{3}$ $(m/s)$

33. Nhiều lựa chọn

Cho hình chóp SABCD với đáy là hình chữ nhật có AB=a, BC= $a \sqrt{2}$ , $S A ⊥ (A B C D)$ và $S A = a \sqrt{3}$ . Gọi M là trung điểm SD và (P) là mặt phẳng đi qua B, M sao cho (P) cắt mặt phẳng $(S A C)$ theo một đường thẳng vuông góc với BM. Khoảng cách từ điểm S đến $(P)$ bằng

A. $\frac{2 a \sqrt{2}}{3}$

B. $\frac{a \sqrt{2}}{9}$

C. $\frac{a \sqrt{2}}{3}$

D. $\frac{4 a \sqrt{2}}{9}$

34. Nhiều lựa chọn

Biết đồ thị hàm số $y = \frac{(2 m - n) x^{2} + m x + 1}{x^{2} + m x + n - 6}$ (m, n là tham số) nhận trục hoành và trục tung làm hai đường tiệm cận. Tính $m + n$ .

A. 6

B. -6

C. 8

D. 9

35. Nhiều lựa chọn

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{x^{2} + 2}{\sqrt{m x^{4} + 3}}$ có một đường tiệm cận ngang.

A. $m < 0$

B. $m > 3$

C. $m = 0$

D. $m > 0$

36. Nhiều lựa chọn

Tìm tất cả các giá trị của tham số m để đồ thị hàm số $y = \frac{x - 1}{\sqrt{2 x^{2} - 2 x - m} - x - 1}$ có đúng bốn đường tiệm cận.

A. $m \in [- 5; 4] \ \{- 4\}$

B. $m \in [- 5; 4]$

C. $m \in (- 5; 4) \ \{- 4\}$

D. $m \in (- 5; 4] \ \{- 4\}$

37. Nhiều lựa chọn

Cho hàm số f(x) có đạo hàm liên tục trên R và có đồ thị của hàm y=f'(x) như hình vẽ. Xét hàm số $g (x) = f (x^{2} - 2)$ . Mệnh đề nào dưới đây sai?

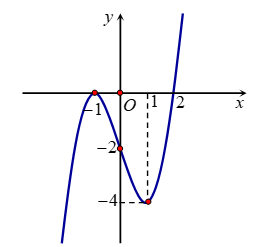
Cho hàm số f(x) có đạo hàm liên tục trên R và có đồ thị của hàm y=f'(x) như hình vẽ. Xét hàm số g(x)= f( x^2-2). Mệnh đề nào dưới đây sai? (ảnh 1)

A. Hàm số $g (x)$ đồng biến trên $(2; + \infty) .$

B. Hàm số $g (x)$ nghịch biến trên $(0; 2) .$

C. Hàm số $g (x)$ nghịch biến trên $(- 1; 0) .$

D. Hàm số $g (x)$ nghịch biến trên $(- \infty; - 2) .$

38. Nhiều lựa chọn

Cho hàm số y=f(x). Biết hàm số y=f'(x) có đồ thị như hình vẽ bên dưới. Hàm số $y = f (3 - x^{2})$ đồng biến trên khoảng

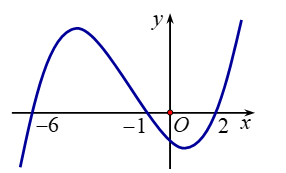
Cho hàm số y=f(x). Biết hàm số y=f'(x) có đồ thị như hình vẽ bên dưới. Hàm số y= f(3-x^2) đồng biến trên khoảng (ảnh 1)

A. $(2; 3)$

B. $(- 2; - 1)$

C. $(- 1; 0)$

D. $(0; 1)$

39. Nhiều lựa chọn

Tìm cực đại của hàm số $y = x \sqrt{1 - x^{2}}$ .

A. $\frac{1}{\sqrt{2}}$

B. $\frac{- 1}{\sqrt{2}}$

C. $- \frac{1}{2}$

D. $\frac{1}{2}$

40. Nhiều lựa chọn

Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số $y = x^{3} - 2 x^{2} + (1 - m) x + m$ có hai điểm cực trị nằm về hai phía đối với trục hoành.

A. $- \frac{1}{4} < m \neq 0$

B. $m > 0$

C. $- \frac{1}{4} < m < 0$

D. $m < - \frac{1}{4}$

41. Nhiều lựa chọn

Trên khoảng $(0; 1)$ hàm số $y = x^{3} + \frac{1}{x}$ đạt giá trị nhỏ nhất tại $x_{0}$ bằng

A. $\frac{1}{2}$

B. $\frac{1}{\sqrt[4]{3}}$

C. $\frac{1}{\sqrt[3]{3}}$

D. $\frac{1}{\sqrt{3}}$

42. Nhiều lựa chọn

Tìm tất cả các giá trị của m để phương trình $x + 1 = m \sqrt{2 x^{2} + 1}$ có hai nghiệm phân biệt.

A. $- \frac{\sqrt{2}}{2} < m < \frac{\sqrt{6}}{6}$

B. $m < \frac{\sqrt{2}}{2}$

C. $m > \frac{\sqrt{6}}{6}$

D. $\frac{\sqrt{2}}{2} < m < \frac{\sqrt{6}}{2}$

43. Nhiều lựa chọn

Cho $\lim_{x \to 1} \frac{x^{2} + a x + b}{x^{2} - 1} = \frac{- 1}{2} (a, b \in ℝ) .$ Tổng $S = a^{2} + b^{2}$ bằng

A. S=13

B. S=9

C. S=4

D. S=1

44. Nhiều lựa chọn

Cho hàm số $y = \frac{2 x - 2}{x - 2}$ có đồ thị là $(C)$ , Mlà điểm thuộc $(C)$ sao cho tiếp tuyến của $(C)$ tại Mcắt hai đường tiệm cận của $(C)$ tại hai điểm A,B, thỏa mãn $A B = 2 \sqrt{5}$ . Gọi S là tổng các hoành độ của tất cả các điểm M thỏa mãn bài toán. Tìm giá trị của S.

A. 6

B. 5

C. 8

D. 7

45. Nhiều lựa chọn

Cho hình chóp tam giác SABC có SA vuông góc với mặt đáy, tam giác ABC cân tại A. Trên cạnh AB lấy điểm D sao cho AB=3AD. Gọi H là hình chiếu của B trên CD, M là trung điểm đoạn thẳng CH. Tính theo a thể tích khối chóp SABM biết $S A = A M = a$ và $B M = \frac{2}{3} a$ .

A. $\frac{\sqrt{3} a^{3}}{9}$

B. $\frac{\sqrt{3} a^{3}}{12}$

C. $\frac{a^{3}}{9}$

D. $\frac{a^{3}}{18}$

46. Nhiều lựa chọn

Cho hàm số $f (x) = x^{4} - (m + 2) x^{3} + m x + 3$ . Trong trường hợp giá trị nhỏ nhất của f(x) đạt giá trị lớn nhất, hãy tính f(3)?

A. 12

B. 27

C. 47

D. 54

47. Nhiều lựa chọn

Thầy Tâm cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng $\frac{500}{3} m^{3}$ . Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ là $500.000$ đồng ${/m}^{2}$ . Khi đó, kích thước của hồ nước như thế nào để chi phí thuê nhân công mà thầy Tâm phải trả thấp nhất:

A. Chiều dài 20m, chiều rộng 15m và chiều cao $\frac{20}{3} m$ .

B. Chiều dài 20m, chiều rộng 10m và chiều cao $\frac{5}{6} m$ .

C. Chiều dài 10m, chiều rộng 5m và chiều cao $\frac{10}{3} m$ .

D. Chiều dài 30m, chiều rộng 15m và chiều cao $\frac{10}{27} m$ .

48. Nhiều lựa chọn

Xét các số thực dương x, y, z thỏa mãn x+y+z=4 và xy+yz+zx=5. Giá trị nhỏ nhất của biểu thức $(x^{3} + y^{3} + z^{3}) (\frac{1}{x} + \frac{1}{y} + \frac{1}{z})$ bằng

A. 20

B. 25

C. 15

D. 35

49. Nhiều lựa chọn

Một người cần làm một hình lăng trụ tam giác đều từ tấm nhựa phẳng để có thể tích là $6 \sqrt{3} {cm}^{3}$ . Để ít hao tốn vật liệu nhất thì cần tính độ dài các cạnh của khối lăng trụ tam giác đều này bằng bao nhiêu?

A. Cạnh đáy bằng $2 \sqrt{6} cm$ và cạnh bên bằng 1cm.

B. Cạnh đáy bằng $2 \sqrt{3} cm$ và cạnh bên bằng 2cm .

C. Cạnh đáy bằng $2 \sqrt{2} cm$ và cạnh bên bằng 3cm.

D. Cạnh đáy bằng $4 \sqrt{3} cm$ và cạnh bên bằng $\frac{1}{2} cm$ .

50. Nhiều lựa chọn

Cho hàm số y=f(x)có bảng biến thiên như sau:

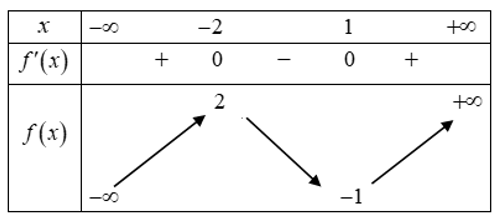
Cho hàm số y=f(x)có bảng biến thiên như sau: Số nghiệm của phương trình f( 3x^4-6x^2+1)=1 là (ảnh 1)