Quiz

Bộ 20 đề thi giữa học kì 1 Toán 12 năm 2022-2023 có đáp án- Đề 15

Admin32 câu hỏiToánLớp 12

Bắt đầu ngay

32 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Tìm m để hàm số $y = 4 x^{3} + m x^{2} - 12 x$ đạt cực tiểu tại điểm x=-2 .

A. $m = - 9$

B. $K h ô n g c ó m .$

C. $m = 9$

D. m=2

2. Nhiều lựa chọn

Cho hàm số $y = - \frac{x^{3}}{3} - m x^{2} - (2 m + 3) x - m$ ( m là tham số). Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên R?

A. 5

B. 3

C. 4

D. 2

3. Nhiều lựa chọn

Cho hình chóp SABCD , có đáy ABCD là hình thang vuông tại A và D , có AB= 2a , AD=DC=a , SA=a và $S A ⊥ (A B C D)$ . của góc giữa hai mặt phẳng (SBC) và $(A B C D)$ là

A. $\sqrt{2}$

B. $\frac{1}{\sqrt{2}}$

C. $\frac{1}{\sqrt{3}}$

D. $\sqrt{3}$

4. Nhiều lựa chọn

Kí hiệu m,M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số $y = \frac{x + 3}{2 x - 1}$ trên đoạn $[1; 4]$ . Tính giá trị của biểu thức $d = M - m$ .

A. $d = 4$

B. d=3

C. d=5

D. d=2

5. Nhiều lựa chọn

Cho lăng trụ tam giác đều ABCA'B'C' có AB=a ; A'B tạo với mặt đáy (ABC) một góc 60 $°$ . Tính thể tích V khối lăng trụ đã cho.

A. $V = \frac{a^{3}}{4}$

B. $V = \frac{3}{2} a^{3}$

C. $V = \frac{3}{4} a^{3}$

D. $V = 3 a^{3}$

6. Nhiều lựa chọn

Mệnh đề nào đúng với bảng biến thiên sau :

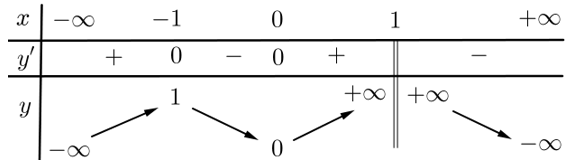
Mệnh đề nào đúng với bảng biến thiên sau : A. Hàm số nghịch biến trên (-1,1) . (ảnh 1)

A. Hàm số nghịch biến trên $(- 1; 1)$ .

B.Hàm số nghịch biến trên $(1; 2)$ .

C. Hàm số đồng biến trên $(0; + \infty)$ .

D. Hàm số đồng biến trên $(- \infty; 1)$ .

7. Nhiều lựa chọn

Cho hình chóp SABC có đáy ABC là tam giác đều cạnh 2a , hai mặt bên (SAB) và (SAC) cùng vuông góc với đáy. Góc giữa cạnh bên SB và mặt phẳng (ABC) là $60 °$ . Tính thể tích V khối chóp SABC .

A. $V = \frac{a^{3} \sqrt{2}}{12}$

B. $V = \frac{a^{3} \sqrt{2}}{3}$

C. $V = a^{3} \sqrt{2}$

D. $V = 2 a^{3}$

8. Nhiều lựa chọn

Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y = \frac{x - m + 2}{x + 1}$ giảm trên các khoảng xác định của nó?

A. $m < - 3$

B. $m \leq - 3$

C. $m < 1$

D. $m \leq 1$

9. Nhiều lựa chọn

Tìm giá trị nhỏ nhất của hàm số $y = x^{4} - 2 x^{2} + 1$ trên đoạn $[0; 3]$ .

A. 64

B. 9

C. 1

D. 0

10. Nhiều lựa chọn

Cho hàm số $(C) : y = x^{3} + 3 x^{2}$ . Phương trình tiếp tuyến của đồ thị (C) tại điểm $M (1; 4)$ là

A. $y = - 9 x + 5$

B. $y = 9 x + 5$

C. $y = 9 x - 5$

D. $y = - 9 x - 5$

11. Nhiều lựa chọn

Cho hàm số $y = \frac{1}{4} x^{4} - \frac{4}{3} x^{3} - \frac{7}{2} x - 2 x - 1$ . Khẳng định nào sau đây đúng?

A. Hàm số có 1 cực đại và 2 cực tiểu.

B. Hàm số có 1 cực tiểu và 2 cực đại,.

C. Hàm số không có cực trị.

D. Hàm số chỉ có 1 cực tiểu và không có cực đại.

12. Nhiều lựa chọn

Cho hàm số y=f(x) được biểu diễn như hình vẽ bên. Đáp án nào đúng về hàm số đã cho?

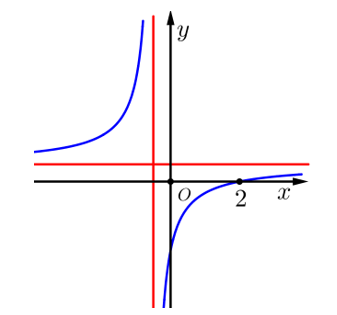
A. $y = \frac{x + 2}{2 x - 1}$

B. $y = \frac{x + 3}{x - 1}$

C. $y = \frac{x - 2}{2 x + 1}$

D. $y = \frac{x - 2}{x + 1}$

13. Nhiều lựa chọn

Cho hàm số $y = - x^{3} + 3 x^{2} - 4$ . Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng $(0; 2)$ .

B. Hàm số nghịch biến trên khoảng $(- \infty; 2)$ .

C. Hàm số đồng biến trên khoảng $(0; + \infty)$ .

D.Hàm số đồng biến trên khoảng $(0; 2)$ .

14. Nhiều lựa chọn

Đường cong ở hình dưới đây là đồ thị của một trong bốn hàm số nào dưới đây?

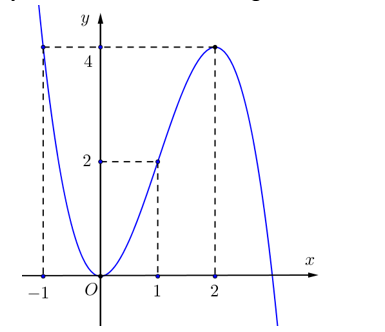
Đường cong ở hình dưới đây là đồ thị của một trong bốn hàm số nào dưới đây? (ảnh 1)

A. $y = - x^{4} + 3 x^{2} + 1$

B. $y = - x^{3} + 3 x^{2}$

C. $y = - x^{3} + 3 x$

D. $y = x^{3} - 3 x^{2}$

15. Nhiều lựa chọn

Hàm số $y = \frac{x^{2} - m x + 1}{x - m}$ có giá trị lớn nhất là 4 trên $(- \infty; m)$ khi m thỏa bất đẳng thức nào sau đây?.

A. $- 4 \leq m \leq 3$

B. $8 \leq m \leq 12$

C. $5 < m < 8$

D. $m \leq - 6$

16. Nhiều lựa chọn

Đáy của lăng trụ đứng tam giác ABCA'B'C' là tam giác đều. Mặt phẳng (A'BC) tạo với đáy một góc 30o và diện tích tam giác A'BC bằng 8. Tính thể tích khối lăng trụ.

A. $8 \sqrt{3}$

B. $4 \sqrt{3}$

C. $16 \sqrt{3}$

D. đáp án khác

17. Nhiều lựa chọn

Cho lăng trụ tam giác ABCA'B'C' có BB'=a, góc giữa đường thẳng BB' và (ABC) bằng $60 °$ , tam giác ABC vuông tại C và góc $\hat{B A C} = 60 °$ . Hình chiếu vuông góc của điểm B' lên (ABC) trùng với trọng tâm của $Δ A B C$ . Thể tích của khối tứ diện theo $A^{'} . A B C$ bằng a

A. $\frac{13 a^{3}}{108}$

B. $\frac{15 a^{3}}{108}$

C. $\frac{7 a^{3}}{106}$

D. $\frac{9 a^{3}}{208}$

18. Nhiều lựa chọn

Hàm số $y = \frac{x - m^{2}}{x + 1}$ có giá trị nhỏ nhất trên [0,1] bằng -1 khi

A. $m = - 1$

B. $m = \pm 1$

C. m=1

D. m=0

19. Nhiều lựa chọn

Tính thể tích khối tứ diện đều cạnh a.

A. $\frac{a^{3} \sqrt{2}}{12}$

B. $\frac{a^{3}}{6}$

C. $a^{3}$

D. $\frac{a^{3} \sqrt{2}}{4}$

20. Nhiều lựa chọn

Đồ thị hàm số nào sau đây có ba đường tiệm cận?

A. $y = \frac{x}{x^{2} - x + 9}$

B. $y = \frac{1}{4 - x^{2}}$

C. $y = \frac{1 - 2 x}{1 + x}$

D. $y = \frac{x + 3}{5 x - 1}$

21. Nhiều lựa chọn

Cho hàm số $y = \frac{m x - 1}{2 x + m}$ . Tìm m để đồ thị hàm số có tiệm cận ngang đi qua điểm $(- 1; \sqrt{2})$ .

A. m=2

B. $m = 2 \sqrt{2}$

C. $m = \frac{\sqrt{2}}{2}$

D. $m = \sqrt{2}$

22. Nhiều lựa chọn

Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a; SA vuông góc với mặt phẳng ( ABC); góc giữa đường thẳng SB và mặt phẳng ( ABC) bằng 60 $°$ . Gọi M là trung điểm của cạnh AB. Tính khoảng cách từ B đến mặt phẳng ( SMC).

A. $\frac{a}{2}$

B. a

C. $\frac{a \sqrt{39}}{13}$

D. $a \sqrt{3}$

23. Nhiều lựa chọn

Hàm số $y = \frac{2 x + 3}{x + 1}$ có bao nhiêu điểm cực trị

A. 0

B. 3

C. 2

D. 1

24. Nhiều lựa chọn

Cho hàm số $y = \frac{2 x + 1}{x - 2}$ có đồ thị là $(C)$ . Tiếp tuyến của $(C)$ song song với đường thẳng $5 x + y - 2 = 0$

A. $y = 5 x + 2$

B. $y = - 5 x + 2$ hoặc $y = - 5 x + 22$

C. $y = - 5 x + 22$

D. $y = - 5 x + 2$

25. Nhiều lựa chọn

Tìm m để hàm số $y = x^{4} + (m + 3) x^{2} + 4$ có 1 cực trị.

A. 0 $m \in [- 3; + \infty)$

B. $m \in (- 3; + \infty)$

C. $m \in (- \infty; - 3]$

D. $m \in (- \infty; - 3)$

26. Nhiều lựa chọn

Hàm số $y = - 2 x^{4} + x^{2} + 1$ có số điểm cực trị là

A. 0

B. 3

C. 2

D. 1

27. Nhiều lựa chọn

Tiệm cận đứng của đồ thị hàm số $y = \frac{x - 5}{x^{2} - x - 6}$ là

A. $x = 1.$

B. $y = - 2; y = 3.$

C. x=1

D. $x = - 2; x = 3.$

28. Nhiều lựa chọn

Hình bên là đồ thị của hàm số nào?

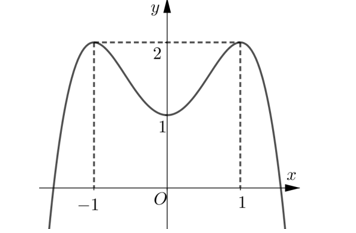
Hình bên là đồ thị của hàm số nào? (ảnh 1)

A. $y = - x^{4} + 2 x^{2} + 1$

B. $y = - x^{4} + 2 x^{2}$

C. $y = x^{4} + 3 x^{2} - 2$

D. $y = - x^{4} + 3 x^{2} + 1$

29. Nhiều lựa chọn

Cho hàm số bậc ba $y = a x^{3} + b x^{2} + c x + d (a \neq 0)$ có đồ thị như hình vẽ

Cho hàm số bậc ba y= ax^3+bx^2+cx+d ( a khác 0) có đồ thị như hình vẽ Mệnh đề nào dưới đây đúng? (ảnh 1)

Mệnh đề nào dưới đây đúng?

A. $a < 0, b > 0, c < 0, d < 0$

B. $a < 0, b < 0, c < 0, d < 0$

C. $a > 0, b > 0, c > 0, d < 0$

D. $a < 0, b > 0, c > 0, d < 0$

30. Nhiều lựa chọn

Cho hình chóp SABC có đáy là tam giác vuông cân tại C , cạnh huyền có độ dài bằng 8a . Gọi M là trung điểm của BC , hình chiếu vuông góc của S xuống mặt phẳng (ABC) là trung điểm H của AM và $S B = \frac{25 a}{2}$ . Khoảng cách từ đến mặt phẳng (ABC) là:

A. $\frac{2 a \sqrt{1042}}{\sqrt{259}}$

B. $\frac{4 a \sqrt{1042}}{\sqrt{259}}$

C. $\frac{a \sqrt{1042}}{\sqrt{259}}$

D. $\frac{a \sqrt{1042}}{2 \sqrt{259}}$

31. Nhiều lựa chọn

Tất cả các giá trị thực của tham số m sao cho hàm số $y = - x^{4} + (2 m - 3) x^{2} + m$ nghịch biến trên khoảng $(1; 2)$ là $(- \infty; \frac{p}{q}]$ , trong đó phân số $\frac{p}{q}$ tối giản và $q > 0$ . Hỏi tổng $p + q$ là

A. 5

B. 9

C. 7

D. 3

32. Nhiều lựa chọn

Có bao nhiêu giá trị nguyên của tham số m để hàm số $y = x^{3} - 3 x^{2} + 2 m x - 1$ có 2 cực trị $x_{1}, x_{2}$ thỏa mãn $|x_{1} - x_{2}| = 2$ ?

A. 1

B. 3

C. 0

D. 2

Gợi ý cho bạn

QuizToán - Tốt nghiệp THPT

Trắc nghiệm củng cố

2 câu hỏi3 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi5 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi28 lượt thi

QuizToán - Lớp 12

10 bài tập Xác định các yếu tố cơ bản của đường thẳng trong không gian có lời giải

10 câu hỏi16 lượt thi

QuizToán - Lớp 12

10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải

10 câu hỏi14 lượt thi

QuizToán - Lớp 12

10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Khoảng cách từ một điểm đến một mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình mặt phẳng đi qua 1 điểm kèm điều kiện song song với mặt phẳng khác có lời giải

10 câu hỏi13 lượt thi

Facebook Youtube