50 CÂU HỎI
Cho hình hộp ABCD.A'B'C'D' Người ta định nghĩa “Mặt chéo của hình hộp là mặt tạo bởi hai đường chéo của hình hộp đó”. Hình hộp ABCD.A'B'C'D' có số mặt chéo là
A. 4
B. 10
C. 8
D. 6
Chọn ngẫu nhiên 6 số nguyên dương trong tập và sắp xếp chúng theo thứ tự tăng dần. Xác suất để số 3 được chọn và xếp ở vị trí thứ hai là
A. .
B. .
C. .
D. .
Số nghiệm của phương trình thuộc đoạn là
A. 5
B. 7
C. 4
D. 6
Cả hai xạ thủ cùng bắn vào bia. Xác suất hai người bắn trúng bia của hai xạ thủ lần lượt là 0,8 và 0,7. Xác suất để cả hai người cùng bắn trượt là
A. 0,06
B. 0,94
C. 0,56
D. 0,44
Tại một buổi lễ có 15 cặp vợ chồng tham dự. Mỗi ông bắt tay một lần với mọi người trừ vợ mình. Các bà không ai bắt tay với
nhau. Hỏi có bao nhiêu cái bắt tay?
A. 210
B. 105
C. 315
D. 78
Cho tứ diện ABCD, G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (ACD) và (GAB) là
A. AH, H là hình chiếu của B trên CD.
B. AM, M là trung điểm của AB.
C. AK, K là hình chiếu của C trên BD.
D. AN, N là trung điểm của CD .
Một hộp đựng 12 bóng đèn, trong đó có 4 bóng đèn bị hỏng. Lấy ngẫu nhiên 3 bóng đèn ra khỏi hộp. Xác suất để trong ba bóng lấy ra có 2 bóng đèn bị hỏng là
A. .
B. .
C. .
D. .
Hàm số xác định với mọi khi
A. .
B. m = 0.
C. .
D. .
Một nhóm học sinh có 4em nữ và 5em nam. Số cách xếp 9em này thành một hàng ngang sao cho giữa hai em nữ bất kỳ đều
không có một em nam nào là
A. 36
B. 2880
C.
D. 17280
Với phương trình có ba em học sinh giải 3 đáp án là
Chọn đáp án đúng
A. Tất cả đều đúng.
B. Chỉ (I) đúng.
C. Chỉ (II) đúng.
D. Chỉ (III) đúng.
Tổng bằng
A. .
B. .
C. .
D. .
Cho hai đường thẳng song song . Trên đường thẳng lấy 10 điểm phân biệt, trên đường thẳng lấy 15 điểm phân biệt. Số tam giác tạo thành mà ba đỉnh của nó được chọn từ 25điểm vừa nói ở trên là
A. .
B. .
C. .
D. .
Trong các hàm số sau, hàm số nào không là hàm số chẵn và cũng không là hàm số lẻ?
A. .
B. .
C. .
D. .
Một bữa tiệc bàn tròn của các câu lạc bộ trong trường THPT Đào Duy Từ có 3 thành viên từ câu lạc bộ múa, 4 thành viên từ câu lạc bộ Tiếng anh và 5 thành viên từ câu lạc bộ Nhảy. Số cách xếp chỗ ngồi cho các thành viên sao cho những người cùng câu lạc bộ ngồi cạnh nhau là
A. 34560.
B. 103680.
C. .
D. 60.
Cho 4điểm A,B,C,D không cùng nằm trong một mặt phẳng. Trên AB,AD lần lượt lấy các điểm M,N sao cho MN cắt BD tại I. Điểm I không thuộc mặt phẳng nào sau đây?
A. (BCD)
B. (ABD)
C. (CMN)
D. (ADC)
Hệ số của trong khai triển là
A. 3003
B. 5005
C. 1
D. 4004
Trong không gian số vị trí tương đối giữa đường thẳng và mặt phẳng là
A. 1
B. 2
C. 3
D. 4
Xác suất sinh con trai trong mỗi lần sinh là 0,51. Xác suất sao cho 3 lần sinh có ít nhất 1 con trai là
A. 0,88
B. 0,22
C. 0,73
D. 0,27
Với giá trị nào của tham số m thì phương trình sinx - m -1 = 0 có nghiệm?
A.
B. .
C.
D.
Hình vẽ nào sau đây biểu diễn đồ thị hàm số
A.
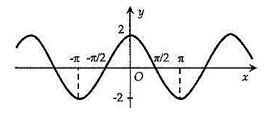
B.
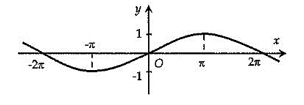
C.
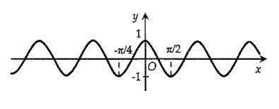
D.
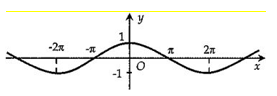
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số là
A. .
B. .
C. .
D. .
Một nhóm học sinh gồm 5 nam và 5 nữ đứng thành hàng ngang. Số cách sắp xếp mà nam, nữ đúng xen kẽ nhau là
A. .
B. .
C. .
D. .
Cho tứ giác lồi ABCD và một điểm Skhông thuộc mp(ABCD). Có nhiều nhất bao nhiêu mặt phẳng xác định bởi các điểm A,B,C,D,S ?
A. 5
B. 6
C. 7
D. 8
Chọn câu đúng?
A. Hai đường thẳng cùng song song với một đường thẳng thứ 3 thì song song với nhau.
B. Không có mặt phẳng nào chứa cả hai đường thẳng a và b thì ta nói a và b chéo nhau.
C. Hai đường thẳng cùng song song với một mặt phẳng thì song song với nhau.
D. Hai đường thẳng song song với nhau nếu chúng không có điểm chung.
Hàm số y = 1 + sinx có chu kì T là:
A. .
B. .
C. .
D. .
Cho hình chóp SABCDvới đáy ABCDlà tứ giác lồi. Hình nào sau đây không thể là thiết diện của hình chóp?
A. Lục giác.
B. Tứ giác.
C. Ngũ giác.
D. Tam giác.
Trên kệ sách có 10 sách Toán khác nhau và 5 sách Văn khác nhau. Lấy lần lượt 3 cuốn sách mà không để lại lên kệ. Xác suất để được hai cuốn sách đều là Văn, cuốn thứ ba là Toán là
A. .
B. .
C. .
D. .
Cho tứ diện ABCD có M,N,P,Q lần lượt là trung điểm của các cạnh AB,AD,CD,BC. Mệnh đề nào sau đây sai?
A. và .
B. và MN=PQ.
C. MNPQ là hình bình hành.
D. MP và NQ chéo nhau.
Cho hình bình hành ABCDvà một điểm Skhông nằm trong mặt phẳng (ABCD). Giao tuyến của hai mặt phẳng (SAB)và (SCD)là một đường thẳng song song với đường thẳng nào sau đây?
A. AB
B. AC
C. BC
D. SA
Nghiệm của phương trình là
A. .
B. .
C. .
D. .
Khi khai triển nhị thức Newton thì ta thấy trong đó xuất hiện hai số hạng 24x và . Giá trị của a và n là
A. a =3,n =7.
B. a = 3,n =8.
C. a =4,n =6.
D. a =2, n = 12.
Trong các mệnh đề sau, mệnh đề nào đúng ?
A. Hàm số y = tanx luôn luôn tăng.
B. Hàm số y =tanx luôn luôn tăng trên từng khoảng của tập xác định.
C. Hàm số y =tanx tăng trong các khoảng .
D. Hàm số y =tanx tăng trong các khoảng .
Tại một khu dân cư, tỉ lệ người mắc bệnh tim là 8%, mắc bệnh huyết áp là 9% và mắc cả hai bệnh đó là 5%. Chọn ngẫu nhiên một người sống tại vùng đó. Xác suất để người đó bị mắc ít nhất một trong hai bệnh tim hoặc huyết áp là
A. 0,12
B. 0,14
C. 0,22
D. 0,07
Cho n là số nguyên dương thỏa mãn . Xét khai triển . Hệ số lớn nhất P(x) là
A. 129024.
B. .
C. .
D. 252.
Có 6 học sinh và 4 thầy giáo sẽ ngồi trên một ghế dài. Số cách xếp chỗ cho 10 người đó sao cho mỗi thầy giáo ngồi giữa hai học sinh là
A. 604800
B. 86400
C. 55012
D. 120960
Cho hình chóp SABCD có đáy là hình bình hành ABCD tâm O. Gọi M,N,P là 3 điểm trên các cạnh AD,CD,SO. Thiết diện của hình chóp với mặt phẳng (MNP) là hình gì?
A. Hình thang.
B. Tứ giác.
C. Ngũ giác.
D. Hình bình hành.
Cho hình chóp SABCD có đáy ABCD là một hình thang với đáy AD và BC. Biết AD = a, BC = b. Gọi I và J lần lượt là trọng tâm các tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB,SC lần lượt tại M,N. Mặt phẳng (BCI) cắt SA,SD tại P,Q. Giả sử AM cắt BP tại E, CQ cắt DN tại F. Tính EF theo a,b.
A. .
B. .
C. .
D. .
Sắp xếp 5 học sinh lớp A và 5 học sinh lớp B vào hai dãy ghế đối diện nhau, mỗi dãy 5 ghế sao cho 2 học sinh ngồi đối diện nhau thì khác lớp. Khi đó số cách xếp là
A. 460500.
B. 460900.
C. 460000.
D. 460800.
Có bao nhiêu số tự nhiên có 6 chữ số khác nhau được lập từ các số sao cho tổng của 3 chữ số đầu nhỏ hơn tổng 3 chữ số cuối 1 đơn vị?
A. 72
B. 216
C. 108
D. 144
Tìm số hạng không chứa x trong khai triển biết là số nguyên dương thỏa mãn .
A. 72864.
B. .
C. .
D. .
Gọi A là tập hợp các số có 5chữ số khác nhau được tạo từ các số . Từ Achọn ngẫu nhiên một số, xác suất số đó có số 3và 4đứng cạnh nhau là
A. .
B. .
C. .
D. .
Số nghiệm của phương trình: trong khoảng là.
A. 2
B. 0
C. 3
D. 1
Từ phòng chuyên môn gồm 15người, trong đó có Việt và Nam, người ta muốn chọn một tổ công tác gồm 5người, trong đó có 11tổ trưởng, 4tổ viên hơn nữa Việt và Nam không đồng thời có mặt trong tổ. Số cách chọn là
A. 13585
B. 4752
C. 2730
D. 2717
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến là đường thẳng a. Trong (P) lấy hai điểm A,Bnhưng không thuộc asao cho ABcắt atại Evà Slà một điểm không thuộc (P). Các đường thẳng SA,SBcắt (Q) tại C,D. Khẳng định nào đúng?
A. AB,CD và a đồng quy.
B. AB,CD và a chéo nhau.
C. AB,CD và a song song với nhau.
D. AB,CD và a trùng nhau.
Từ các chữ số thuộc tập hợp có thể lập được bao nhiêu số tự nhiên chẵn có năm chữ số khác nhau và chia hết cho 9?
A. 24
B. 48
C. 120
D. 72
Phương trình (m là tham số thực) có nghiệm khi và chỉ khi
A. .
B. .
C. .
D. .
Một bài trắc nghiệm có 10 câu hỏi, mỗi câu hỏi có 4 phương án lựa chọn trong đó có 1 đáp án đúng. Giả sử mỗi câu trả lời đúng được 5 điểm và mỗi câu trả lời sai bị trừ đi 2 điểm. Một học sinh không học bài nên đánh hú họa mỗi câu hỏi một phương án trả lời. Xác suất để học sinh này nhận điểm dưới 1 là:
A. .
B. .
C. .
D. .
Cho hình chóp SABCD có đáy là hình thang ABCD, . Gọi I là giao điểm của AB và DC, M là trung điểm SC, DM cắt mặt phẳng (SAB) tại J. Khẳng định nào sau đây sai?
A. S,I,J thẳng hàng.
B. .
C. .
D. .
Cho hình hộp ABCD.A'B'C'D'. Các điểm M,Ntương ứng trên các đoạn sao cho . Tỉ số bằng
A. 2
B. 3
C. 4
D. 1
Cho tứ diện ABCDvà M,Nlà các điểm trên cạnh AB,CDsao cho và Plà một điểm trên cạnh AC. Tỉ số diện tích tam giác MNPvà diện tích thiết diện của tứ diện cắt bởi mặt phẳng (MNP)bằng
A. .
B. .
C. .
D. .

