39 CÂU HỎI
bằng
A. .
B. .
C. .
D.
Họ tất cả các nguyên hàm của hàm số là
A. .
B. .
C. .
D. .
bằng
A. .
B. .
C. .
D.
bằng
A. .
B. .
C. .
D.
bằng
A. .
B. .
C. .
D.
bằng
A. .
B. .
C. .
D. .
Cho hàm số f(x) thỏa mãn và . Tính .
A. .
B. .
C. .
D. .
Biết rằng g(x) là một nguyên hàm của và , tính .
A. 0.
B. .
C. .
D. 1.
Tính .
A. .
B. .
C. .
D. .
Cho . Khi đó bằng
A. .
B.
C. .
D. .
bằng
A. 12.
B. 4.
C. -12.
D. 8.
bằng
A. .
B. .
C. .
D.
Biết rằng với , hãy tính .
A. .
B. .
C. .
D. .
Cho hàm số sao cho liên tục trên R, và Tính .
A. .
B. .
C. .
D. .
Biết với . Tính .
A. .
B. .
C. .
D. .
Giả sử hàm số f(x) liên tục và dương trên đoạn thỏa mãn . Tính tích phân .
A. .
B. .
C. .
D. .
Cho hàm số f(x) có đồ thị như hình vẽ bên dưới.
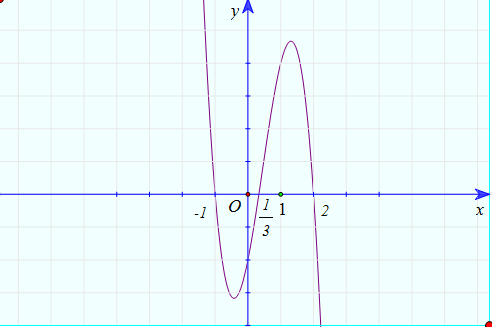
Diện tích hình phẳng giới hạn bởi đồ thị hàm số f(x) và trục Ox được tính theo công thức nào sau đây?
A. .
B. .
C. .
D. .
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục Ox.
A. .
B. .
C. .
D. .
Gọi là diện tích của hình phẳng giới hạn bởi parabol và đường thẳng Ta có
A.
B.
C.
D.
Hình vẽ dưới đây là một mảnh vườn hình Elip có bốn đỉnh là là các hình chữ nhật; , . Biết rằng kinh phí trồng hoa là đồng/ , hãy tính số tiền (làm tròn đến hàng đơn vị) dùng để trồng hoa trên phần gạch sọc.
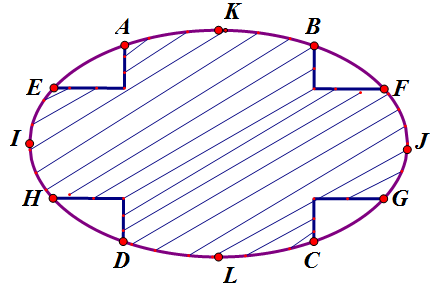
A. đồng.
B. đồng.
C. đồng.
D. đồng.
Một quần thể virut Corona P đang thay đổi với tốc độ , trong đó t là thời gian tính bằng giờ. Quần thể virut Corona P ban đầu (khi ) có số lượng là 1000 con. Số lượng virut Corona sau 3 giờ gần với số nào sau đây nhất?
A. 16000.
B. 21750.
C. 12750.
D. 11750.
Cho hình (H) giới hạn bởi đồ thị hàm số , trục hoành, các đường thẳng . Biết rằng khối tròn xoay do (H) quay quanh trục Ox tạo ra có thể tích là . Giá trị của a là
A. 6.
B. 2.
C. 4.
D. 8.
Cho hình (H) giới hạn bởi đồ thị hàm số , , các đường thẳng . Biết rằng khối tròn xoay do (H) quay quanh trục Ox tạo ra có thể tích là , hỏi rằng có bao nhiêu số nguyên nằm trong khoảng ?
A. 6.
B. 7.
C. 8.
D. 9.
Cho hình thang cong giới hạn bởi đồ thị hàm số , trục hoành, các đường thẳng x = 1 và x = 4. Thể tích của khối tròn xoay được tạo thành khi quay hình thang cong trên quanh trục Ox bằng
A. .
B. .
C. .
D. .
Cho a, b là hai số thực dương. Gọi (H) là hình phẳng giới hạn bởi parabol và đường thẳng . Quay (H) quanh trục hoành thu được khối có thể tích là V1, quay (H) quanh trục tung thu được khối có thể tích là V2. Tìm sao cho .
A. .
B. .
C. .
D. .
Trong không gian Oxyz, cho . Nếu thì có tọa độ là
A. .
B. .
C. .
D. .
Trong không gian Oxyz, cho hai điểm , . Độ dài đoạn thẳng AB bằng
A. .
B. .
C. .
D. 2.
Trong không gian , cho mặt cầu . Tìm tọa độ tâm và bán kính của mặt cầu .
A. và .
B. và .
C. và .
D. và .
Trong không gian Oxyz cho hai điểm ,. Phương trình mặt cầu (S) có tâm B và A đi qua là
A. .
B. .
C. .
D. .
Trong không gian Oxyz cho hai điểm , . Phương trình mặt cầu (S) có đường kính AB là
A.
B.
C.
D.
Thể tích khối cầu ngoại tiếp tứ diện đều ABCD cạnh a là
A. .
B. .
C. .
D. .
Trong không gian cho Oxyz, , (a>0, b>0, c>0). Diện tích tam giác ABC bằng Tìm khoảng cách từ B đến mặt phẳng (ACD) khi đạt giá trị lớn nhất.
A. .
B. .
C. .
D. .
Trong không gian Oxyz, cho hai điểm . Mặt phẳng trung trực của AB đoạn thẳng có phương trình là
A. .
B. .
C. .
D. .
Trong không gian , gọi là mặt phẳng đi qua điểm , đồng thời vuông góc với hai mặt phẳng và . Phương trình của là
A. .
B. .
C. .
D. .
Trong không gian Oxyz, cho mặt cầu (S): . Mặt phẳng (P) tiếp xúc (S) với tại điểm có phương trình là
A. .
B. .
C. .
D. .
Trong không gian Oxyz, cho ba điểm , . Khi đó mặt phẳng (ABC) có phương trình là
A. .
B. .
C. .
D. .
Trong không gian , mặt phẳng trùng với mặt phẳng nào dưới đây ?
A. .
B. .
C. .
D. .
Trong không gian Oxyz, cho bốn điểm , , , . Tính khoảng cách từ M đến mặt phẳng (ABC).
A. .
B. .
C. .
D. .
Trong không gian , cho mặt phẳng và hai điểm , . Gọi sao cho và góc có số đo lớn nhất. Khi đó đẳng thức nào sau đây đúng?
A. .
B. .
C. .
D. .

