39 CÂU HỎI
Cho hàm số f(x) là một nguyên hàm của hàm số trên R. Số điểm cực trị của hàm số là:
A. 1.
B. 2.
C. 3.
D. 4.
Hàm số nào dưới đây nghịch biến trên R?
A. .
B. .
C. .
D. .
Mệnh đề nào dưới đây đúng?
A. .
B. .
C. .
D. .
Trong không gian toạ độ Oxyz ,cho hai điểm A(-2;1;2) và L(1;-1;0). Tìm toạ độ điểm C thuộc trục hoành sao cho vuông tại B.
A. .
B. .
C. .
D. .
Phương trình 4sinxcosx = 1 có bao nhiêu nghiệm thuộc khoảng ?
A. 6.
B. 2.
C. 4.
D. 8.
Hàm số nào dưới đây có điểm cực trị?
A. .
B..
C. .
D. .
Đồ thị của hàm số nào dưới đây không có điểm chung với trục hoành
A. .
B. .
C. .
D. .
Cho khối lăng trụ ABC.A'B'C' có thể tích bằng và diện tích tam giác ABC bằng . Khoảng cách từ điểm A' đến mặt phẳng (ABC) theo a.
A. 6a.
B. .
C. 2a.
D. .
Giải bất phương trình trên R tập số thực ta được tập hợp nghiệm là khoảng (m;n). Tính tổng m + n.
A. .
B. .
C. .
D. .
Giải bất phương trình trên tập số thưc R.
A. .
B. .
C. .
D. .
Tập giá trị của hàm số là
A. .
B. .
C. R.
D. .
Hàm số nào dưới đây có tập xác định là khoảng ?
A. .
B. .
C. .
D. .
Cho f(x) à g(x) là các hàm số thỏa mãn điều kiện . Khẳng định nào say đây đúng?
A. .
B. .
C. .
D. .
Cho a số thực dương thỏa mãn điều kiện . Tìm giá trị nhỏ nhất của biểu thức .
A. 4.
B. 3.
C. -4.
D. -3.
Tìm tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt.
A. .
B. R.
C. .
D. .
Khẳng định nào dưới đây sai?
A. là hằng số.
B. là hằng số.
C. là hằng số.
D. là hằng số.
Cho hàm số , với a là tham số thực. Mệnh đề nào dưới đây sai?
A. Nếu a < 0 thì hàm số đã cho có ba điểm cực trị.
B. Hàm số đã cho luôn có điểm cực trị.
C. Nếu a > 0 thì hàm số đã cho không có điểm cực đại.
D. Nếu hàm số đã cho có duy nhất một điểm cực trị thì a là số dương.
Viết phương trình tiếp tuyến của đồ thị hàm số y = lnx tại điểm có hoành độ bằng 1.
A. .
B. .
C. .
D. .
Trong không gian tọa độ Oxyz, tính khoảng cách từ điểm A(0;-1;2) đến trục tung.
A. .
B. 1.
C. 2.
D. .
Cho số dương a thỏa mãn điều kiện . Có bao nhiêu số nguyên thuộc đoạn ?
A. 5.
B. 4.
C. 3.
D. 2.
Cho hình chóp đều có đáy là tam giác đều có chiều cao bằng độ dài cạnh đáy. Tính với là góc giữa mặt bên và mặt đáy của hình chóp dã cho.
A. .
B. .
C. .
D. .
Tìm số tự nhiên n thỏa mãn điều kiện .
A. .
B. .
C. .
D. .
Cho hàm số y = f(x) có tập xác định , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: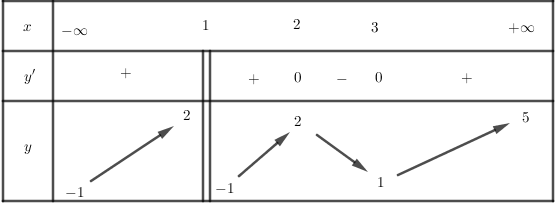
Khẳng định nào dưới đây sai?
A. Đồ thị hàm số y = f(x) không có tiệm cận đứng.
B. Đồ thị hàm số y = f(x) không có tiệm cận ngang.
C.Tập giá trị của hàm số y = f(x) là khoảng (-1;5).
D. Hàm số y = f(x) có một điểm cực đại và một điểm cực tiểu.
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình bình hành, AD = a, là trung điểm của CC'. Tính khoảng cách giữa hai đường thẳng AD' và B'M, biết rằng diện tích hình bình hành ABCD bằng .
A. 2a.
B. a.
C. .
D. .
Trong không gian Oxyz, tìm tọa độ điểm H là hình chiếu vuông góc của điểm A(1;2;3) trên mặt phẳng .
A. .
B. .
C. .
D. .
Cho x, y là hai số thực thỏa mãn các điều kiện và . Tính tổng x + 2y.
A. .
B. .
C. .
D. .
Cho lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi, , AB = 2a.Tính khoảng cách giữa hai đường thẳng AA' và BD' theo a.
A. a.
B. .
C. .
D. .
Trong không gian tọa độ Oxyz, cho hai điểm A(-2;0;0) và B(0;5;0). Tính diện tích tam giác OAB (O là gốc tọa độ).
A. 2.
B. 10.
C. .
D. 5.
Một con quạ khát nước, nó tìm thấy một cái lọ có nhiều nước và cột nước bên trong là một khối trụ với bán kính đáy bằng 2 cm. Nhưng mỏ quạ chưa đủ dài để uống được nước trong lọ. Thấy một cậu bé bỏ rơi rất nhiều bi (khối cầu) bán kính 0,5 cm ngoài sân, quạ liền nhặt những viên bi đó bỏ vào lọ cho nước dâng lên. Mặt nước trong lọ cần dâng lên ít nhất nữa thì quạ mới uống được. Hỏi quạ cần nhặt ít nhất 1 (cm) bao nhiêu viên bi bỏ vào lọ để uống được 4 ml nước?
A. 30.
B. 32.
C. 25.
D. 31.
Cho hàm số , với m là tham số. Gọi M là tập hợp tất cả các giá trị thực của tham số m để khoảng cách từ gốc tọa độ O đến đường tiệm cận đứng của đồ thị hàm số đã cho bằng 2. Số phần tử của tập hợp M là:
A. 2.
B. 1.
C. 4.
D. 3.
Cho F(x) và G(x) là các nguyên hàm của hàm số f(x) trên R. Khẳng định nào dưới đây sai?
A. .
B. .
C. Hàm số là một nguyên hàm f(x) của hàm số trên R.
D. .
Khối trụ có bán kính đáy bằng , chiều cao bằng và thể tích bằng ; Khối trụ có bán kính đáy bằng , chiều cao bằng và thể tích bằng . Tính biết rằng , .
A. .
B. .
C. .
D. .
Tìm hệ số của số hạng chứa trong khai triển biểu thức .
A. 990.
B. 1782.
C. -297.
D. 198.
Trong không gian tọa độ Oxyz, cho mặt phẳng có phương trình 2x - y + z = 0. Nếu vectơ là vectơ pháp tuyến của mặt phẳng thì
A. .
B. .
C. .
D. .
Cho số thực m thỏa mãn điều kiện . Tính
A. 1.
B. 0.
C. .
D. -1.
Cho hình chóp S.ABC có cạnh bên , AB = AC = 3 cm, , SA = 4 cm .Gọi M là trung điểm của cạnh SA; (S) là mặt cầu ngoại tiếp tứ diện ABCM; , . Tính thể tích của khối tứ diện MNPS.
A. .
B. .
C. .
D. .
Tìm tất cả các giá trị của tham số m để đồ thị hàm số không có tiệm cận ngang.
A. Không có giá trị m thỏa mãn yêu cầu.
B. .
C. .
D. .
Trong không gian tọa độ Oxyz, cho hai điểm A(1;2;-1) và B(2;1;0). Khi điểm N di động trên mặt phẳng tọa độ Oxyz thì giá trị lớn nhất của biểu thức là:
A. .
B. 5.
C. .
D. 8.
Đề thi Tốt nghiệp THPT môn Toán năm 2018 gồm 50 câu trắc nghiệm và mỗi câu có 4 phương án để lựa chọn (trong đó có 1 phương án đúng), số điểm mỗi câu là 0,2 (không phẩy hai). Thí sinh Nguyễn Văn Chuẩn đã làm và chọn đúng được 45 câu, vì sắp hết thời gian làm bài nên Chuẩn quyết định chọn đáp án ngẫu nhiên ở 5 câu còn lại. Tính xác suất để bài thi của Chuẩn đạt từ 9,8 (chín phẩy tám) điểm trở lên.
A.
B.
C.
D.

