Bộ 12 đề thi học kì 2 Toán 7 Cánh Diều cấu trúc mới có đáp án - Đề 06
30 câu hỏi
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Biểu đồ sau cho biết số lượng các loại sách có trong thư viện của một trường.
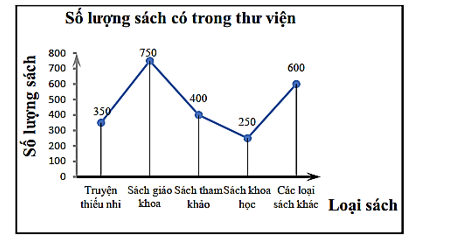
Số loại sách có số lượng ít hơn \(700\) quyển là
\(3.\)
\(4.\)
\(5.\)
\(2.\)
Một hộp có 12 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số \(1,2,3,....,12\) hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp, tập hợp \(M\) gồm các kết quả có thể cảy ra đối với sự kiện “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” là
\(M = \left\{ {1,2,3,....,12} \right\}.\)
\(M = \left\{ {1;3;6;9;12} \right\}.\)
\(M = \left\{ {6;9;12} \right\}.\)
\(M = \left\{ {3;6;9;12} \right\}.\)
Diện tích hình chữ nhật có chiều dài \(a{\rm{ }}\left( {{\rm{cm}}} \right)\) và chiều rộng \(5{\rm{ }}\left( {{\rm{cm}}} \right)\) là
\(5a{\rm{ }}\left( {{\rm{cm}}} \right).\)
\(2\left( {a + 5} \right){\rm{ }}\left( {{\rm{cm}}} \right).\)
\(2\left( {a + 5} \right){\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
\(5a{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Biểu thức đại số biểu thị tích của hai số tự nhiên liên tiếp là
\(n\left( {n + 1} \right)\) với \(n \in \mathbb{N}.\)
\(2k\left( {k + 2} \right)\) với \(k \in \mathbb{N}.\)
\(x\left( {y + 1} \right)\) với \(x,y \in \mathbb{N}.\)
\(\left( {x + 1} \right)\left( {y + 1} \right)\) với \(x,y \in \mathbb{N}.\)
Kết quả của phép chia \(6{x^4}:\left( { - 2{x^3}} \right)\) bằng
\( - 12x.\)
\(3{x^7}.\)
\( - 3x.\)
\(3x.\)
Số nào sau đây là nghiệm của đa thức \(P\left( x \right) = 3x + 9\)?
\( - 9.\)
\( - 3.\)
\(3.\)
\(9.\)
Nếu tam giác \(MNP\) vuông tại \(M\) có \(\widehat N = 30^\circ \) thì
\(NP < MP < MN.\)
\(MP < MN < NP.\)
\(MN < NP < MP.\)
\(MP < NP < MN.\)
Chọn cụm từ thích hợp điền vào chỗ trống:
“Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu lớn hơn thì…..”
lớn hơn.
nhỏ hơn.
ngắn nhất.
bằng nhau.
Cho \(\Delta ABC = \Delta MNK\) và biết \(\widehat A = 35^\circ ,\widehat N = 45^\circ \). Số đo góc \(K\) là:
\(80^\circ .\)
\(100^\circ .\)
\(40^\circ .\)
\(180^\circ .\)
Một tam giác cân có số đo góc ở đáy gấp hai lần số đo góc ở đỉnh. Số đo góc ở đáy của tam giác cân đó là
\(72^\circ .\)
\(65^\circ .\)
\(56^\circ .\)
\(60^\circ .\)
Cho điểm \(M\) thuộc đường trung trực của đoạn thẳng \(AB\). Biết \(MA = 7{\rm{ cm,}}\) độ dài đoạn thẳng \(MB\) là
\(7{\rm{ cm}}{\rm{.}}\)
\({\rm{3,5 cm}}{\rm{.}}\)
\({\rm{14 cm}}{\rm{.}}\)
\({\rm{5 cm}}{\rm{.}}\)
Cho tam giác \(ABC\) có góc \(A\) tù, trực tâm của tam giác \(ABC\) nằm ở vị trí
Bên trong tam giác.
Bên ngoài tam giác.
Trên một cạnh của tam giác.
Trùng với đỉnh \(A\) của tam giác.
a) Số các kết quả có thể xảy ra là \(10.\)
b) Biến cố “Số được chọn là bội của 11” là biến cố ngẫu nhiên.
c) Xác suất của biến cố “Số được chọn có dạng \(2k{\rm{ }}\left( {k \in \mathbb{N},0 < k < 11} \right)\)” là 1.
d) Xác suất của biến cố “Số được chọn là ước của \(32\)” là \(\frac{1}{2}.\)
a) \(\Delta ADB = \Delta EDB\).
b) \(ED > DC.\)
c) \(AD < DC.\)
d) \(D\) là trực tâm của \(\Delta BCE.\)
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Chọn ngẫu nhiên một số tự nhiên có hai chữ số. Tính xác suất để số được chọn chia hết cho \(5\) nhưng không chia hết cho \(2\). (Kết quả ghi dưới dạng số thập phân)
Tìm giá trị nhỏ nhất của biểu thức \(A = {\left( {2x - 3} \right)^2} + {\left( {y - \frac{1}{2}} \right)^2} + 2017\).
Cho đa thức \(f\left( x \right) = {x^3} - a{x^2} - 9x + b\). Biết rằng đa thức nhận các giá trị \(1\) và \(3\) làm nghiệm. Tìm giá trị của nghiệm còn lại của đa thức \(f\left( x \right).\)
Cho \(\Delta ABC,\) \(\widehat A = 80^\circ ,AB = AC.\) \(M\) là điểm nằm trong tam giác sao cho \(\widehat {MBC} = 10^\circ ,\) \(\widehat {MCB} = 30^\circ \). Tính số đo của \(\widehat {AMB}\).
a) Thu gọn đa thức \(K\left( x \right)\). Tính \(K\left( 1 \right)\).
b) Tính \(P\left( x \right) - K\left( x \right)\).
c) Tìm đa thức \(H\left( x \right)\) sao cho \(H\left( x \right) + 2K\left( x \right) = P\left( x \right)\).
a) Chứng minh \(\Delta ABH = \Delta ACH.\)
b) Qua \(C\) kẻ đường thẳng song song với \(AD\), đường thẳng này cắt tia \(BE\) tại \(F.\) Chứng minh \(EH = EF.\)
c) Gọi \(G\) là giao điểm của \(FD\) với \(CH.\) Chứng minh \(HG = \frac{2}{3}HE.\)








