Bộ 12 đề thi học kì 2 Toán 7 Cánh Diều cấu trúc mới có đáp án - Đề 12
6 câu hỏi
Số học sinh đạt điểm giỏi môn Toán trong 4 tháng học kì I của khối lớp 7 được biểu diễn bởi đồ thị đoạn thẳng sau:
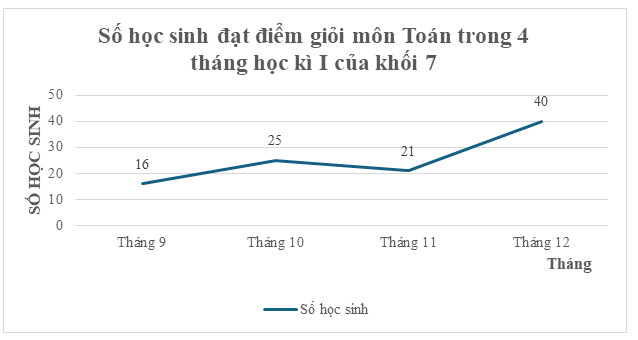
a) Lập bảng dữ liệu theo mẫu sau:
Tháng | 9 | 10 | 11 | 12 |
Số học sinh đạt điểm giỏi môn Toán |
|
|
|
|
b) Từ tháng 9 đến tháng 10, số học sinh đạt điểm giỏi môn Toán của khối lớp 7 tăng bao nhiêu học sinh?
c) Số học sinh đạt điểm giỏi môn Toán tháng 11 giảm bao nhiêu phần trăm so với tháng 10?
Có hai chiếc hộp, hộp \(A\) đựng 5 quả bóng ghi các số \(1;3;5;7;9\); hộp \(B\) đựng 5 quả bóng ghi các số \(2;4;6;8;10\). Lấy ngẫu nhiên một quả bóng từ mỗi hộp. Xét các biến cố sau:
\(M\): “Tổng các số ghi trên hai quả bóng lớn hơn 2”.
\(N\): “Tích các số ghi trên hai quả bóng bằng 30”.
\(P\): “Chênh lệch giữa hai số ghi trên hai quả bóng bằng 10”.
a) Trong các biến cố trên, hãy chỉ ra biến cố nào là biến cố chắc chắn, biến cố nào là biến cố không thể.
b) Lấy ngẫu nhiên một quả bóng từ hộp \(A\). Tính xác suất của biến cố \(Q\): “Số ghi trên quả bóng là số nguyên tố”.
c) Lấy ngẫy nhiên một quả bóng từ hộp \(B\). Tính xác suất của biến cố \(T\): “Số ghi trên quả bóng là ước của 16”.
Một hình vuông có độ lớn một cạnh là \(x{\rm{ }}\left( {{\rm{cm}}} \right)\), tam giác vuông cân có độ lớn cạnh góc vuông là \(y{\rm{ }}\left( {{\rm{cm}}} \right)\).
a) Viết biểu thức biểu thị tổng diện tích của hình vuông và tam giác vuông cân.
b) Tính tổng diện tích của hình vuông và của tam giác vuông cân khi \(x = 2\) và \(y = 4.\)
Cho đa thức \(A\left( x \right) = \frac{1}{4}{x^3} + \frac{{11}}{3}{x^2} - 6x - \frac{2}{3}{x^2} + \frac{7}{4}{x^3} + 2x + 3\);
a) Thu gọn và sắp xếp đa thức \(A\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Xác định bậc và hệ số cao nhất của đa thức \(A\left( x \right)\).
c) Tìm \(n\) biết \({2^n} = A\left( { - 1} \right)\).
d) Cho \(B\left( x \right) = \left( {{x^2} - x + 1} \right)\left( {2x + 3} \right)\).
Tính \(C\left( x \right) = A\left( x \right) - B\left( x \right)\). Tìm nghiệm của đa thức \(C\left( x \right)\).
5.1. Cho \[\Delta ABD\] cân tại \[A\] có \[\widehat A = 40^\circ \]. Trên tia đối của tia \[DB\] lấy điểm \[C\] sao cho \[DC = DA\]. Tính số đo của \[\widehat {ACB}\].
5.2. Cho \(\Delta ABC\) vuông tại \(A\) (\(AB < AC\)). Tia phân giác của \(\widehat B\) cắt \(AC\) tại \(D\). Kẻ \(DE\) vuông góc với \(BC\) tại \(E\). Gọi \(M\) là giao điểm của \(AB\) và \(DE\).
a) Chứng minh \(\Delta ABD = \Delta EBD\), từ đó suy ra \(BA = BE\).
b) So sánh độ dài các cạnh của \(\Delta ADM\).
c) Gọi \(K\) là trung điểm của \(MC\). Chứng minh ba điểm \(B\), \(D\), \(K\) thẳng hàng.
Mật mã của một chiếc két sắt nhà Trang là một số có ba chữ số và được lập từ các chữ số \(1,2,3\). Mẹ Trang muốn mở khóa két sắt mà quên mất mật mã. Tính xác suất để mẹ Trang mở 1 lần đúng mật mã.








